Transformacja Möbiusa - Möbius transformation

W geometrii i złożonej analizy , A funkcja homograficzna na płaszczyźnie zespolonej jest funkcją wymierną od formy

{\ Displaystyle f (z) = {\ Frac {az + b} {cz + d}}}

jednej zmiennej zespolonej z ; tutaj współczynniki a , b , c , d są liczbami zespolonymi spełniającymi ad − bc ≠ 0.

Geometrycznie transformację Möbiusa można uzyskać wykonując najpierw projekcję stereograficzną z płaszczyzny na jednostkę dwukulową , obracając i przesuwając kulę do nowego położenia i orientacji w przestrzeni, a następnie wykonując projekcję stereograficzną (z nowej pozycji kuli ) do samolotu. Te przekształcenia zachowują kąty, mapują każdą prostą linię na linię lub okrąg i mapują każdy okrąg na linię lub okrąg.

Przemiany Mobius są rzutowe transformacje o skomplikowanej linii projekcyjnej . Tworzą one grupę zwaną grupą Möbiusa , która jest rzutową grupą liniową PGL(2, C ). Wraz ze swoimi podgrupami ma liczne zastosowania w matematyce i fizyce.

Transformacje Möbiusa zostały nazwane na cześć Augusta Ferdynanda Möbiusa ; są też różnie nazwane homographies , Przekształcenia homograficzne , liniowych przekształceń ułamkowych , dwuliniowe transformacje , ułamkowe transformacje liniowe lub przekształcenia wirowania (teoria względności) .

Przegląd

Transformacje Möbiusa są definiowane na rozszerzonej płaszczyźnie zespolonej (tj. płaszczyźnie zespolonej powiększonej o punkt w nieskończoności ). ${\ Displaystyle {\ widehat {\ mathbb {C}}} = \ mathbb {C} \ filiżanka \ {\ infty \}}$

Rzut stereograficzny utożsamia się ze sferą, zwaną wówczas sferą Riemanna ; alternatywnie można ją traktować jako złożoną linię rzutową . Transformacje Möbiusa są dokładnie bijektywnymi mapami konformalnymi ze sfery Riemanna na nią samą, tj. automorfizmami sfery Riemanna jako złożonej rozmaitości ; alternatywnie są to automorfizmy odmiany algebraicznej. Dlatego zbiór wszystkich przekształceń Möbiusa tworzy grupę pod kompozycją . Ta grupa nazywana jest grupą Möbiusa i czasami jest oznaczana . ${\widehat {\mathbb {C}}}$ ${\widehat {\mathbb {C}}}$ ${\ Displaystyle \ mathbb {C} \ mathbb {P} ^ {1}}$ ${\ Displaystyle \ mathbb {C} \ mathbb {P} ^ {1}}$ ${\ Displaystyle \ operatorname {Aut} ({\ widehat {\ mathbb {C}}})}$

Grupa Möbiusa jest izomorficzna z grupą orientacji-konserwowanie izometrii o hiperbolicznej 3-przestrzeni i dlatego odgrywa ważną rolę przy badaniu hiperboliczne 3-rozmaitości .

W fizyce , składnikiem tożsamości z grupy Lorentza działa na sferze niebieskiej w taki sam sposób, że grupa Möbiusa działa na sferze Riemanna. W rzeczywistości te dwie grupy są izomorficzne. Obserwator, który przyspiesza do prędkości relatywistycznych, zobaczy, jak wzór konstelacji widziany w pobliżu Ziemi nieustannie przekształca się zgodnie z nieskończenie małymi transformacjami Möbiusa. Ta obserwacja jest często traktowana jako punkt wyjścia teorii twistora .

Pewne podgrupy grupy Möbiusa tworzą grupy automorfizmu innych prosto połączonych powierzchni Riemanna ( płaszczyzny zespolonej i płaszczyzny hiperbolicznej ). Jako takie, transformacje Möbiusa odgrywają ważną rolę w teorii powierzchni Riemanna . Podstawowym grupa każdej powierzchni Riemanna jest dyskretna podgrupa grupy Möbius (patrz grupę Fuchsian i grupę Kleinian ). Szczególnie ważną dyskretną podgrupą grupy Möbius jest grupa modułowa ; ma kluczowe znaczenie dla teorii wielu fraktali , form modularnych , krzywych eliptycznych i równań Pellianowskich .

Transformacje Möbiusa można ogólniej zdefiniować w przestrzeniach o wymiarze n > 2 jako bijective konforemne mapy zachowujące orientację od n -sfery do n -sfery. Taka transformacja jest najogólniejszą formą mapowania konforemnego domeny. Zgodnie z twierdzeniem Liouville'a transformację Möbiusa można wyrazić jako złożenie translacji, podobieństw , transformacji ortogonalnych i inwersji.

Definicja

Ogólna forma transformacji Möbiusa jest podana przez

{\ Displaystyle f (z) = {\ Frac {az + b} {cz + d}}}

gdzie a , b , c , d są liczbami zespolonymi spełniającymi

ad - bc \neq 0

. Jeśli

ad = bc

, zdefiniowana powyżej funkcja wymierna jest stałą ponieważ

{\ Displaystyle f (z) = {\ Frac {az + b} {cz + d}} = {\ Frac {a (cz + d)} {c (cz + d)}} - {\ Frac {reklama- bc}{c(cz+d)}}={\frac {a}{c}}}

i dlatego nie jest uważany za transformację Möbiusa.

W przypadku $c \neq 0$ , definicja ta jest rozszerzona na całą sferę Riemanna przez zdefiniowanie

{\ Displaystyle f \ lewo ({\ Frac {-d} {c}} \ prawej) = \ infty {\ tekst {i}} f (\ infty) = {\ Frac {a} {c}}.}

Jeśli $c = 0$ , definiujemy

f(\infty)=\infty.

Zatem transformacja Möbiusa jest zawsze bijektywną funkcją holomorficzną od sfery Riemanna do sfery Riemanna.

Zbiór wszystkich przekształceń Möbiusa tworzy grupę pod kompozycją . Grupie tej można nadać strukturę rozmaitości zespolonej w taki sposób, że kompozycja i inwersja są mapami holomorficznymi . Grupa Möbiusa jest wtedy złożoną grupą Liego . Grupa Möbiusa jest zwykle oznaczana, ponieważ jest to grupa automorfizmu sfery Riemanna. ${\ Displaystyle \ operatorname {Aut} ({\ widehat {\ mathbb {C}}})}$

Punkty stałe

Każda transformacja Möbiusa bez tożsamości ma dwa stałe punkty na sferze Riemanna. Zauważ, że punkty stałe są tutaj liczone z krotnością ; transformacje paraboliczne to te, w których punkty stałe pokrywają się. Jeden lub oba te punkty stałe mogą być punktem w nieskończoności. ${\ Displaystyle \ gamma _ {1} \ gamma _ {2}}$

Wyznaczanie punktów stałych

Stałe punkty transformacji

{\ Displaystyle f (z) = {\ Frac {az + b} {cz + d}}}

są otrzymywane przez rozwiązanie równania punktu stałego f ( γ ) = γ . Dla c ≠ 0 ma to dwa pierwiastki otrzymane przez rozwinięcie tego równania do

{\ Displaystyle c \ gamma ^ {2} - (reklama) \ gamma -b = 0 \ ,}

i zastosowanie wzoru kwadratowego . Korzenie są

{\ Displaystyle \ gamma _ {1,2} = {\ Frac {(reklama) \ pm {\ sqrt {\ lewo (reklama \ prawo) ^ {2} + 4 bc}} {2c}} = {\ Frac { (reklama)\pm {\sqrt {\Delta }}}{2c}}}

z wyróżnikiem

{\ Displaystyle \ Delta = (\ operatorname {tr} {\ mathfrak {H}}) ^ {2}-4 \ det {\ mathfrak {H}} = (a + d) ^ {2}-4 (reklama- pne).}

Transformacje paraboliczne mają przypadkowe stałe punkty ze względu na zerowy dyskryminator. Dla c niezerowego i niezerowego dyskryminatora transformacja jest eliptyczna lub hiperboliczna.

Gdy c = 0, równanie kwadratowe degeneruje się w równanie liniowe, a transformacja jest liniowa. Odpowiada to sytuacji, w której jednym z punktów stałych jest punkt w nieskończoności. Gdy a ≠ d drugi punkt stały jest skończony i jest dany przez

{\ Displaystyle \ gamma =-{\ Frac {b} {reklama}}.}

W tym przypadku transformacja będzie prostą transformacją złożoną z translacji , obrotów i dylatacji :

z\mapsto \alfa z+\beta.

Jeśli c = 0 i a = d , to oba punkty stałe są w nieskończoności, a transformacja Möbiusa odpowiada czystej translacji:

z\mapsto z+\beta.

Dowód topologiczny

Topologicznie fakt, że transformacje Möbiusa (nietożsamości) ustalają 2 punkty (z wielokrotnością) odpowiada charakterystyce Eulera sfery wynoszącej 2:

{\ Displaystyle \ chi ({\ kapelusz {\ mathbb {C}}}) = 2.}

Po pierwsze, projekcyjna grupa liniowa PGL(2, K ) jest ostro 3-przechodnia – dla dowolnych dwóch uporządkowanych trójek różnych punktów istnieje unikalna mapa, która przenosi jedną trójkę do drugiej, tak jak w przypadku przekształceń Möbiusa, i tym samym dowód algebraiczny (zasadniczo liczenie wymiarów , ponieważ grupa jest trójwymiarowa). Tak więc każda mapa, która ustala co najmniej 3 punkty, jest tożsamością.

Następnie można zobaczyć, identyfikując grupę Möbiusa z tym, że każda funkcja Möbiusa jest homotopiczna do tożsamości. Rzeczywiście, każdy członek ogólnej grupy liniowej może zostać zredukowany do mapy tożsamości przez eliminację Gaussa-Jordana, co pokazuje, że projekcyjna grupa liniowa jest również połączona ze ścieżką, zapewniając homotopię mapie tożsamości. Twierdzenie Lefschetza-Hopfa stwierdza, że suma wskaźników (w tym kontekście krotności) punktów stałych mapy ze skończenie wieloma punktami stałymi jest równa liczbie Lefschetza mapy, która w tym przypadku jest śladem mapy tożsamości na grupach homologii, co jest po prostu cechą Eulera. ${\ Displaystyle \ operatorname {PGL} (2 \ mathbb {C})}$

Natomiast rzutowa grupa liniowa rzeczywistej linii rzutowej, PGL(2, R ) nie musi ustalać żadnych punktów – na przykład nie ma (rzeczywistych) stałych punktów: jako transformacja złożona ustala ± i – podczas gdy mapa 2 x ustala dwa punkty 0 i ∞. Odpowiada to faktowi, że charakterystyka Eulera okręgu (rzeczywista prosta rzutowa) wynosi 0, a zatem twierdzenie Lefschetza o punkcie stałym mówi tylko, że musi on ustalić co najmniej 0 punktów, a być może więcej. ${\ Displaystyle (1+x)/(1-x)}$

Forma normalna

Transformacje Möbiusa są również czasami zapisywane w kategoriach ich stałych punktów w tak zwanej formie normalnej . Najpierw zajmiemy się przypadkiem nieparabolicznym, dla którego istnieją dwa różne punkty stałe.

Przypadek nieparaboliczny :

Każda transformacja nieparaboliczna jest sprzężona z dylatacją/rotacją, czyli transformacją postaci

z\mapsto kz

( k ∈ C ) ze stałymi punktami na 0 i ∞. Aby to zobaczyć, zdefiniuj mapę

{\ Displaystyle g (z) = {\ Frac {z-\ gamma _ {1}} {z- \ gamma _ {2}}}}

który wysyła punkty ( γ ₁ , γ ₂ ) do (0, ∞). Tutaj zakładamy, że γ ₁ i γ ₂ są różne i skończone. Jeśli jeden z nich jest już w nieskończoności, to g można zmodyfikować tak, aby ustalić nieskończoność i wysłać drugi punkt do 0.

Jeśli f ma różne punkty stałe ( γ ₁ , γ ₂ ) to transformacja ma punkty stałe na 0 i ∞ i dlatego jest dylatacją: . Można wtedy zapisać równanie punktu stałego dla przekształcenia f ${\ Displaystyle gfg ^ {-1}}$ ${\ Displaystyle gfg ^ {-1} (z) = kz}$

{\ Displaystyle {\ Frac {f (z) - \ gamma _ {1} {f (z) - \ gamma _ {2}}} = k {\ Frac {z - \ gamma _ {1}} {z -\gamma _{2}}}.}

Rozwiązanie dla f daje (w postaci macierzowej):

{\ Displaystyle {\ mathfrak {H}} (k; \ gamma _ {1}, \ gamma _ {2}) = {\ zacząć {pmatrix} \ gamma _ {1}-k \ gamma _ {2} i ( k-1)\gamma _{1}\gamma _{2}\\1-k&k\gamma _{1}-\gamma _{2}\end{pmatrix}}}

lub jeśli jeden z punktów stałych znajduje się w nieskończoności:

{\ Displaystyle {\ mathfrak {H}} (k; \ gamma, \ infty) = {\ zacząć {pmatrix} k i (1-k) \ gamma \ \ 0 i 1 \ koniec {pmatrix}}.}

Z powyższych wyrażeń można obliczyć pochodne f w stałych punktach:

f”(\gamma_{1})=k

oraz

{\ Displaystyle f '(\ gamma _ {2}) = 1 / k.}

Zauważmy, że, biorąc pod uwagę porządkuje stałych punktach, możemy wyróżnić jeden z mnożników ( k ) o f jako charakterystycznej stałej z f . Odwrócenie kolejności punktów stałych jest równoznaczne z przyjęciem odwrotnego mnożnika dla stałej charakterystycznej:

{\ Displaystyle {\ mathfrak {H}} (k; \ gamma _ {1}, \ gamma _ {2}) = {\ mathfrak {H}} (1/k; \ gamma _ {2}, \ gamma _ {1}).}

Dla przekształceń loksodromicznych, gdy | k | > 1, mówi się, że γ ₁ jest odpychającym punktem stałym, a γ ₂ jest przyciągającym punktem stałym. Dla | k | < 1, role są odwrócone.

Przypadek paraboliczny :

W przypadku parabolicznym istnieje tylko jeden punkt stały γ . Transformacja wysyłająca ten punkt do ∞ to

{\ Displaystyle g (z) = {\ Frac {1} {z-\ gamma}}}

lub tożsamość, jeśli γ jest już w nieskończoności. Transformacja ustala nieskończoność i dlatego jest translacją:

{\ Displaystyle gfg ^ {-1}}

{\ Displaystyle gfg ^ {-1} (z) = z + \ beta \,.}

Tutaj β nazywamy długością translacji . Wzór na punkt stały dla przekształcenia parabolicznego to zatem

{\ Displaystyle {\ Frac {1} {f (z) - \ gamma}} = {\ Frac {1} {z - \ gamma}} + \ beta.}

Rozwiązanie dla f (w postaci macierzowej) daje

{\ Displaystyle {\ mathfrak {H}} (\ beta; \ gamma ) = {\ zacząć {pmatrix} 1 + \ gamma \ beta & - \ beta \ gamma ^ {2} \ \ \ beta & 1 \ gamma \ beta \end{pmacierz}}}

lub, jeśli γ = ∞:

{\ Displaystyle {\ mathfrak {H}} (\ beta; \ infty ) = {\ zacząć {pmatrix} 1 i \ beta \ \ 0 i 1 \ koniec {pmatrix}}}

Zauważ, że β nie jest stałą charakterystyczną f , która zawsze wynosi 1 dla przekształcenia parabolicznego. Z powyższych wyrażeń można obliczyć:

f”(\gamma)=1.

Polacy transformacji

Punkt nazywany jest słup z ; jest to punkt, który jest przekształcany do punktu w nieskończoności pod . ${\textstyle z_{\infty }=-{\frac {d}{c}}}$ ${\ Displaystyle {\ mathfrak {H}}}$ ${\ Displaystyle {\ mathfrak {H}}}$

Biegun odwrotny to punkt, do którego przekształcany jest punkt w nieskończoności. Punkt w połowie drogi między dwoma biegunami jest zawsze taki sam, jak punkt w połowie między dwoma stałymi punktami: ${\textstyle Z_{\infty }={\frac {a}{c}}}$

{\ Displaystyle \ gamma _ {1} + \ gamma _ {2} = z_ {\ infty} + Z_ {\ infty}.}

Te cztery punkty są wierzchołkami równoległoboku, który jest czasami nazywany charakterystycznym równoległobokiem transformacji.

Przekształcenie można określić za pomocą dwóch stałych punktów γ ₁ , γ ₂ i bieguna . ${\ Displaystyle {\ mathfrak {H}}}$ $z_{\infty}$

{\ Displaystyle {\ mathfrak {H}} = {\ zacząć {pmatrix} Z_ {\ infty} i - \ gamma _ {1} \ gamma _ {2} \ \ 1 i z_ {\ infty} \ koniec {pmatrix} },\;\;Z_{\infty }=\gamma _{1}+\gamma _{2}-z_{\infty }.}

To pozwala nam wyprowadzić wzór na konwersję między k a danym : $z_{\infty}$ ${\ Displaystyle \ gamma _ {1} \ gamma _ {2}}$

{\ Displaystyle Z_ {\ Infty} = {\ Frac {K \ Gamma _ {1} - \ Gamma _ {2} {1-k}}}

{\ Displaystyle k = {\ Frac {\ gamma _ {2}-z_ {\ infty}}{\ gamma _ {1}-z_ {\ infty}}} = {\ Frac {Z_ {\ infty} - \ gamma _{1}}{Z_{\infty }-\gamma _{2}}}={\frac {ac\gamma _{1}}{ac\gamma _{2}}},}

co sprowadza się do

{\ Displaystyle k = {\ Frac {(a + d) + {\ sqrt {\ lewo (reklama \ prawo) ^ {2} + 4BC}} {(a + d) - {\ sqrt {\ lewo (reklama) \right)^{2}+4bc}}}}.}

Ostatnie wyrażenie pokrywa się z jednym z (wzajemnie wzajemnych) stosunków wartości własnych macierzy ${\textstyle {\frac {\lambda _{1}}{\lambda _{2}}}}$

{\ Displaystyle {\ mathfrak {H}} = {\ zacząć {pmatrix} a&b\\c&d\koniec {pmatrix}}}

reprezentujący transformację (porównaj dyskusję w poprzedniej sekcji na temat stałej charakterystycznej transformacji). Jego wielomian charakterystyczny jest równy

{\ Displaystyle \ DET (\ Lambda I_ {2} - {\ Mathfrak {H}}) = \ Lambda ^ {2} - \ Operatorname {tr} {\ Mathfrak {H}} \ \ Lambda + \ DET {\ mathfrak {H}}=\lambda ^{2}-(a+d)\lambda +(ad-bc)}

który ma korzenie

{\ Displaystyle \ lambda _ {i} = {\ Frac {(a + d) \ pm {\ sqrt {\ lewo (reklama \ prawo) ^ {2} + 4BC}}} {2}} = {\ Frac { (a+d)\pm {\sqrt {\left(a+d\right)^{2}-4(ad-bc)}}}{2}}=c\gamma _{i}+d\, .}

Proste przekształcenia i kompozycja Möbiusa

Transformacja Möbiusa może składać się z sekwencji prostych transformacji.

Następujące proste transformacje są również transformacjami Möbiusa:

${\ Displaystyle f (z) = z + b \ quad (a = 1, c = 0, d = 1)}$ jest tłumaczeniem .
${\ Displaystyle f (z) = az \ quad (b = 0, c = 0, d = 1)}$ jest kombinacją a ( homotetyczności i rotacji ). Jeśli to rotacja, jeśli to homotetyka. $|a|=1$ ${\ Displaystyle a \ w \ mathbb {R} }$
${\ Displaystyle f (z) = 1 / z \ quad (a = 0, b = 1, c = 1, d = 0)}$ ( odwrócenie i odbicie względem osi rzeczywistej)

Kompozycja prostych przekształceń

Jeżeli , niech: $c\neq 0$

$f_{1}(z)=z+d/c\quad$ ( Tłumaczenie przez d / c )
$f_{2}(z)=1/z\quad$ ( odwrócenie i odbicie względem osi rzeczywistej)
${\ Displaystyle f_ {3} (z) = {\ Frac {BC-ad} {c ^ {2}}} z \ quad}$ ( homotetyka i rotacja )
$f_{4}(z)=z+a/c\quad$ (tłumaczenie przez a / c )

Następnie funkcje te można skomponować , dając

f_{4}\circ f_{3}\circ f_{2}\circ f_{1}(z)=f(z)={\frac {az+b}{cz+d}}.

To jest,

{\ Displaystyle {\ Frac {az + b} {cz + d}} = {\ Frac {a} {c}} + {\ Frac {e} {z + {\ Frac {d} {c}}}}, }

z

{\ Displaystyle e = {\ Frac {BC-reklama} {c ^ {2}}}.}

Ten rozkład sprawia, że wiele właściwości transformacji Möbiusa staje się oczywistych.

Podstawowe właściwości

Transformacja Möbiusa jest odpowiednikiem sekwencji prostszych transformacji. Kompozycja sprawia, że wiele właściwości transformacji Möbiusa jest oczywistych.

Wzór na odwrotną transformację

Istnienie odwrotnej transformacji Möbiusa i jej wyraźny wzór można łatwo wywnioskować przez złożenie funkcji odwrotnych prostszych transformacji. Oznacza to, że określenie funkcji g ₁ , g ₂ , g ₃ , g ₄ tak, że każdy g _i jest odwrotnością f _I . Następnie kompozycja

{\ Displaystyle g_ {1} \ circ g_ {2} \ circ g_ {3} \ circ g_ {4} (z) = f ^ {-1} (z) = {\ Frac {dz-b} {-cz +a}}}

daje wzór na odwrotność.

Zachowanie kątów i uogólnionych okręgów

Z tego rozkładu widzimy, że transformacje Möbiusa przenoszą wszystkie nietrywialne właściwości odwrócenia okręgu . Na przykład zachowanie kątów sprowadza się do udowodnienia, że odwrócenie okręgu zachowuje kąty, ponieważ inne rodzaje przekształceń to dylatacje i izometrie (translacja, odbicie, obrót), które w trywialny sposób zachowują kąty.

Co więcej, transformacje Möbiusa mapują uogólnione okręgi na uogólnione okręgi, ponieważ odwrócenie okręgu ma tę właściwość. Okrąg uogólniony to okrąg lub linia, przy czym ta ostatnia jest uważana za okrąg przechodzący przez punkt w nieskończoności. Zauważ, że transformacja Möbiusa niekoniecznie mapuje okręgi na okręgi i linie na linie: może mieszać te dwa. Nawet jeśli odwzorowuje okrąg na inny okrąg, niekoniecznie odwzorowuje środek pierwszego okręgu na środek drugiego okręgu.

Zachowanie współczynnika krzyżowego

Stosunki krzyżowe są niezmienne w transformacjach Möbiusa. Oznacza to, że jeśli transformacja Möbiusa mapuje odpowiednio cztery różne punkty na cztery różne punkty , to $z_{1},z_{2},z_{3},z_{4}$ $w_{1},w_{2},w_{3},w_{4}$

{\frac {(z_{1}-z_{3})(z_{2}-z_{4})}{(z_{2}-z_{3})(z_{1}-z_{ 4})}}={\frac {(w_{1}-w_{3})(w_{2}-w_{4})}{(w_{2}-w_{3})(w_{1} -w_{4})}}.

Jeśli jeden z punktów jest punktem w nieskończoności, to stosunek krzyżowy należy określić, przyjmując odpowiednią granicę; np. współczynnik krzyżowy is $z_{1},z_{2},z_{3},z_{4}$ $z_{1},z_{2},z_{3},\infty$

{\frac {(z_{1}-z_{3})}{(z_{2}-z_{3})}}.

Stosunek krzyżowy czterech różnych punktów jest rzeczywisty wtedy i tylko wtedy, gdy przechodzi przez nie linia lub okrąg. To kolejny sposób na pokazanie, że transformacje Möbiusa zachowują uogólnione kręgi.

Koniugacja

Dwa punkty z ₁ i z ₂ są sprzężone w odniesieniu do uogólnionego okręgu C , jeśli dany uogólniony okrąg D przechodzący przez z ₁ i z ₂ i przecinający C w dwóch punktach a i b , ( z ₁ , z ₂ ; a , b ) są w harmonicznym stosunku krzyżowym (tj. ich stosunek krzyżowy wynosi −1). Ta właściwość nie zależy od wyboru okręgu D . Ta właściwość jest również czasami określana jako symetryczna względem linii lub okręgu.

Dwa punkty z , z ^∗ są sprzężone względem prostej, jeśli są symetryczne względem prostej. Dwa punkty są sprzężone w stosunku do okręgu, jeśli są wymieniane przez inwersję względem tego okręgu.

Punkt z ^∗ sprzężony z z, gdy L jest linią wyznaczoną przez wektor oparty e ^iθ w punkcie z _0, można wyraźnie podać jako

{\ Displaystyle z ^ {*} = e ^ {2i \ theta} {\ overline {z-z_ {0}}} + z_ {0}.}

Punkt z ^∗ sprzężony z z, gdy C jest okręgiem o promieniu r wyśrodkowanym z ₀ można wyraźnie podać jako

{\ Displaystyle Z ^ {*} = {\ Frac {R ^ {2}} {\ overline {Z_ Z_ {0}}}} + Z_ {0}}

Ponieważ transformacje Möbiusa zachowują uogólnione koła i proporcje krzyżowe, zachowują również koniugację.

Reprezentacje macierzy projekcyjnej

Naturalne działanie PGL(2, C ) na zespoloną prostą rzutową CP ¹ jest dokładnie naturalnym działaniem grupy Möbiusa na sferę Riemanna, gdzie linia rzutowa CP ¹ i sfera Riemanna są identyfikowane w następujący sposób:

[z_{1}:z_{2}]\\grubość [z_{1}/z_{2},\1].

Tutaj [ z ₁ : z ₂ ] są jednorodnymi współrzędnymi na CP ¹ ; punkt [1:0] odpowiada punktowi ∞ sfery Riemanna. Korzystając z jednorodnych współrzędnych, wiele konkretnych obliczeń dotyczących transformacji Möbiusa można uprościć, ponieważ nie są wymagane żadne rozróżnienia przypadków dotyczące ∞.

Z każdą odwracalną złożoną macierzą 2×2

{\ Displaystyle {\ mathfrak {H}} = {\ zacznij {pmatrix} a & c \ \ b i d \ koniec {pmatrix}}}

możemy skojarzyć transformację Möbiusa

{\ Displaystyle [z, \ 1] {\ zacząć {pmatrix} a & c \ \ b i d \ koniec {pmatrix}} \ = \ [az + b, \ cz + d] \ = \ \ lewo [{\ Frac {az + b}{cz+d}},\ 1\prawo]\ =\ f(z).}

Warunek ad − bc ≠ 0 jest równoważny warunkowi, że wyznacznik powyższej macierzy jest niezerowy, czyli macierz odwracalna.

Łatwo jest sprawdzić, czy wtedy iloczyn dwóch macierzy będzie powiązany ze złożeniem dwóch odpowiednich transformacji Möbiusa. Innymi słowy, mapa

{\ Displaystyle \ pi \ dwukropek \ operatorname {GL} (2 \ mathbb {C}) \ do \ operatorname {Aut} ({\ widehat {\ mathbb {C}}})}

z ogólnej grupy liniowej GL(2, C ) do grupy Möbiusa, która wysyła macierz do przekształcenia f , jest homomorfizmem grupowym .

{\ Displaystyle {\ mathfrak {H}}}

Zauważ, że każda macierz uzyskana przez pomnożenie przez złożony skalar λ określa tę samą transformację, więc transformacja Möbiusa określa swoją macierz tylko

do wielokrotności skalarnych. Innymi słowy: jądro z

Õ

obejmuje wszystkie skalarnych wielokrotności macierzy jednostkowej I , a pierwszy izomorfizmu twierdzenia stanów teorii grupy tak, że grupa iloraz GL (2 C ) / (( C \ {0}) I ) stanowi izomorficzny z grupą Möbiusa. Ta grupa ilorazowa jest znana jako rzutowa grupa liniowa i jest zwykle oznaczana jako PGL(2, C ).

{\ Displaystyle {\ mathfrak {H}}}

\operatorname {Aut} ({\widehat {\mathbb {C}}})\cong \operatorname {PGL} (2,\mathbb {C}).

Ta sama identyfikacja PGL(2, K ) z grupą ułamkowych przekształceń liniowych i grupą projekcyjnych automorfizmów liniowych linii projekcyjnej zachowuje nad każdym ciałem K , fakt interesujący algebraiczny, szczególnie dla ciał skończonych, chociaż przypadek największe znaczenie geometryczne mają liczby zespolone.

Jeśli ograniczymy się do macierzy zdeterminowanej, to odwzorowanie

π

ogranicza się do surjektywnego odwzorowania ze specjalnej grupy liniowej SL(2, C ) do grupy Möbiusa; w układzie ograniczonym jądro jest utworzone przez plus i minus tożsamość, a grupa ilorazowa SL(2, C ) / {± I }, oznaczona przez PSL(2, C ), jest zatem również izomorficzna z grupą Möbiusa:

{\ Displaystyle {\ mathfrak {H}}}

\operatorname {Aut} ({\widehat {\mathbb {C}}})\cong \operatorname {PSL} (2,\mathbb {C}).

Z tego widzimy, że grupa Möbiusa jest 3-wymiarową złożoną grupą Liego (lub 6-wymiarową rzeczywistą grupą Liego). Jest to półprosty nie- zwarta grupa Lie.

Zauważ, że istnieją dokładnie dwie macierze z wyznacznikiem jednostki, które mogą być użyte do reprezentowania dowolnej danej transformacji Möbiusa. Oznacza to, że SL(2, C ) jest podwójną osłoną PSL(2, C ). Ponieważ SL(2, C ) jest po prostu podłączony , jest to uniwersalna osłona grupy Möbius. Dlatego podstawową grupą grupy Möbiusa jest Z ₂ .

Określanie przekształcenia przez trzy punkty

Mając zbiór trzech różnych punktów z ₁ , z ₂ , z ₃ na sferze Riemanna i drugi zbiór różnych punktów w ₁ , w ₂ , w ₃ , istnieje dokładnie jedna transformacja Möbiusa f ( z ) z f ( z _i ) = w _i dla i = 1,2,3. (Innymi słowy: działanie grupy Möbiusa na sferze Riemanna jest ostro 3-przechodnie .) Istnieje kilka sposobów wyznaczenia f ( z ) z danych zbiorów punktów.

Mapowanie najpierw do 0, 1, ∞

Łatwo sprawdzić, czy transformacja Möbiusa

f_{1}(z)={\frac {(z-z_{1})(z_{2}-z_{3})}{(z-z_{3})(z_{2}- z_{1})}}

z matrycą

{\mathfrak {H}}_{1}={\rozpocznij{pmatrix}z_{2}-z_{3}&-z_{1}(z_{2}-z_{3})\\z_ {2}-z_{1}&-z_{3}(z_{2}-z_{1})\end{pmatrix}}

mapuje odpowiednio z ₁ , z ₂ , z ₃ do 0, 1, ∞. Jeżeli jedno z Z _i jest ∞, wtedy właściwa formuła jest otrzymywany z powyższym jednym najpierw podziału wszystkie wpisy, Z _ı i biorąc graniczną Z. _i → ∞.

{\mathfrak {H}}_{1}

Jeśli jest podobnie zdefiniowana do odwzorowywania

w ₁ , w ₂ , w ₃ na 0, 1, ∞, to macierz odwzorowująca z _1,2,3 na w _1,2,3 staje się

{\mathfrak {H}}_{2}

{\ Displaystyle {\ mathfrak {H}}}

{\ Displaystyle {\ mathfrak {H}} = {\ mathfrak {H}} _ {2} ^ {-1} {\ mathfrak {H}} _ {1}.}

Stabilizator {0, 1, ∞} (jako zbiór nieuporządkowany) to podgrupa znana jako grupa anharmoniczna .

Wyraźna formuła wyznacznika

Równanie

{\ Displaystyle w = {\ Frac {az + b} {cz + d}}}

jest odpowiednikiem równania standardowej hiperboli

cwz-az+dw-b=0

w płaszczyźnie ( z , w ). Problem skonstruowania transformacji Möbiusa odwzorowującej trójkę na inną trójkę jest zatem równoważny ze znalezieniem współczynników a , b , c , d hiperboli przechodzącej przez punkty . Wyraźne równanie można znaleźć, oceniając wyznacznik

{\ Displaystyle {\ mathfrak {H}} (z)}

(z_{1},z_{2},z_{3})

(w_{1},w_{2},w_{3})

{\ Displaystyle (z_ {i}, w_ {i})}

\det {\zacząć{pmatrix}zw&z&w&1\\z_{1}w_{1}&z_{1}&w_{1}&1\\z_{2}w_{2}&z_{2}&w_{2}&1 \\z_{3}w_{3}&z_{3}&w_{3}&1\end{pmatrix}}\,

za pomocą rozszerzenia Laplace'a wzdłuż pierwszego rzędu. Daje to w wyniku formuły determinanty

a=\det {\zaczynać{pmatrix}z_{1}w_{1}&w_{1}&1\\z_{2}w_{2}&w_{2}&1\\z_{3}w_{3 }&w_{3}&1\end{pmatrix}}

b=\det {\rozpocznij{pmatrix}z_{1}w_{1}&z_{1}&w_{1}\\z_{2}w_{2}&z_{2}&w_{2}\\z_ {3}w_{3}&z_{3}&w_{3}\end{pmatrix}}

c=\det {\rozpocznij{pmatrix}z_{1}&w_{1}&1\\z_{2}&w_{2}&1\\z_{3}&w_{3}&1\end{pmatrix}}

d=\det {\zacząć{pmatrix}z_{1}w_{1}&z_{1}&1\\z_{2}w_{2}&z_{2}&1\\z_{3}w_{3 }&z_{3}&1\end{pmatrix}}

dla współczynników a,b,c,d macierzy reprezentującej . Skonstruowana macierz ma wyznacznik równy, który nie znika, jeśli z _i odpowiednio. w _i są parami różne, więc transformacja Möbiusa jest dobrze zdefiniowana. Jeśli jeden z punktów z _i lub w _i jest ∞, to najpierw dzielimy wszystkie cztery determinanty przez tę zmienną, a następnie przyjmujemy granicę, gdy zmienna zbliża się do ∞.

{\ Displaystyle {\ mathfrak {H}} = {\ zacząć {pmatrix} a&b\\c&d\koniec {pmatrix}}}

{\ Displaystyle {\ mathfrak {H}}}

(z_{1}-z_{2})(z_{1}-z_{3})(z_{2}-z_{3})(w_{1}-w_{2})(w_{ 1}-w_{3})(w_{2}-w_{3})

Podgrupy grupy Möbius

Jeśli wymagamy, aby współczynniki a , b , c , d transformacji Möbiusa były liczbami rzeczywistymi z ad − bc = 1 , otrzymujemy podgrupę grupy Möbiusa oznaczoną jako PSL(2, R ) . Jest to grupa tych transformacji Möbiusa, które mapują górną półpłaszczyznę H = x + i y : y > 0 na siebie i jest równa grupie wszystkich map biholomorficznych (lub równoważnie: bijective , konforemnych i zachowujących orientację) H → H . Jeśli wprowadzi się odpowiednią metrykę , górna półpłaszczyzna staje się modelem płaszczyzny hiperbolicznej H ² , półpłaszczyznowym modelem Poincarégo , a PSL(2, R ) jest grupą wszystkich zachowujących orientację izometrii H ² w tym Model.

Podgrupa wszystkich transformacji Möbiusa, które mapują otwarty dysk D = z : | z | < 1 do siebie składa się ze wszystkich przekształceń postaci

{\ Displaystyle f (z) = e ^ {i \ phi} {\ Frac {z + b} {{\ bar {b}} z + 1}}}

gdzie ∈ R , b ∈ C i | b | < 1. Jest to grupa wszystkich map biholomorficznych (lub równoważnie: bijektywnych, zachowujących kąt i zachowujących orientację) D → D . Wprowadzając odpowiednią metrykę, otwarty dysk zamienia się w inny model płaszczyzny hiperbolicznej, model dysku Poincarégo , a grupa ta jest grupą wszystkich zachowujących orientację izometrii H ² w tym modelu.

\phi

Ponieważ oba z powyższych podgrup służyć jako grupy izometrii o H ² są izomorficzne. Konkretny izomorfizm jest podany przez koniugację z transformacją

{\ Displaystyle f (z) = {\ Frac {z + i} {iz + 1}}}

który bijective odwzorowuje otwarty dysk jednostki do górnej połowy płaszczyzny.

Alternatywnie rozważmy otwarty dysk o promieniu r , wyśrodkowany na r i . Model dysku Poincarégo na tym dysku staje się identyczny z modelem górnej połowy płaszczyzny, gdy r zbliża się do ∞.

Ilość zwarty podgrupa grupy Möbius jest przez (

Tóth 2002 )

{\ Displaystyle {\ Mathcal {M}}}

{\ Displaystyle {\ mathcal {M}} _ {0}: = \ lewo \ {z \ mapsto {\ Frac {uz-{\ bar {v}}} {vz + {\ bar {u}}}}: | u|^{2}+|v|^{2}=1\prawo\},}

i odpowiada pod izomorfizmie do rzutowej specjalnego jednostkowej grupy zasilacza (2 C ), który jest izomorficzny w szczególnym ortogonalne grupy SO (3) obrotów w trzech wymiarach i może być interpretowane jako obrotów sfery Riemanna. Każda skończona podgrupa jest sprzężona w tę maksymalnie zwartą grupę, a zatem odpowiadają one dokładnie grupom wielościennym, grupom punktowym w trzech wymiarach .

{\ Displaystyle {\ mathcal {M}} \ cong \ operatorname {PSL} (2 \ mathbb {C})}

Grupy Icosahedral transformacji Möbiusa zostały użyte przez Felixa Kleina do uzyskania analitycznego rozwiązania równania kwintycznego w ( Klein 1888 ); współczesna ekspozycja znajduje się w ( Tóth 2002 ).

Jeśli wymagamy, aby współczynniki a , b , c , d transformacji Möbiusa były liczbami całkowitymi z ad − bc = 1, otrzymujemy grupę modułową PSL(2, Z ), dyskretną podgrupę PSL(2, R ) ważną w badanie sieci w płaszczyźnie zespolonej, funkcji eliptycznych i

krzywych eliptycznych . Dyskretne podgrupy PSL(2, R ) są znane jako grupy fuchsowskie ; są ważne w badaniach powierzchni Riemanna .

Klasyfikacja

Pokazano transformację hiperboliczną. Preobrazy okręgu jednostkowego to okręgi Apoloniusza o stosunku odległości c / a oraz ogniskach w − b / a i − d / c .

Dla tych samych ognisk − b / a i − d / c czerwone kółka odwzorowują promienie przechodzące przez źródło.

W dalszej dyskusji będziemy zawsze zakładać, że macierz reprezentująca jest znormalizowana w taki sposób, że . ${\ Displaystyle {\ mathfrak {H}}}$ ${\ Displaystyle \ det {\ mathfrak {H}} = ad-BC = 1}$

Transformacje Möbiusa

nieidentyfikujące są powszechnie klasyfikowane na cztery typy: paraboliczne , eliptyczne , hiperboliczne i loksodromiczne , przy czym hiperboliczne są podklasą loksodromicznych. Klasyfikacja ma znaczenie zarówno algebraiczne, jak i geometryczne. Geometrycznie różne typy prowadzą do różnych przekształceń płaszczyzny zespolonej, co ilustrują poniższe rysunki.

Te cztery typy można rozróżnić patrząc na ślad . Zauważ, że ślad jest niezmienny w

koniugacji , to znaczy

{\ Displaystyle \ operatorname {tr} {\ mathfrak {H}} = a + d}

{\ Displaystyle \ operatorname {tr} \ {\ mathfrak {GHG}} ^ {-1} = \ operatorname {tr} \ {\ mathfrak {H}}}

tak więc każdy członek klasy sprzężonej będzie miał ten sam ślad. Każdą transformację Möbiusa można zapisać w taki sposób, że reprezentująca ją macierz ma wyznacznik (poprzez pomnożenie wpisów przez odpowiedni skalar). Dwie transformacje Möbiusa (obie nie równe transformacji tożsamości) z są sprzężone wtedy i tylko wtedy, gdy

{\ Displaystyle {\ mathfrak {H}}}

{\ Displaystyle {\ mathfrak {H}}, {\ mathfrak {H}} '}

\det {\mathfrak {H}}=\det {\mathfrak {H}}'=1

{\ Displaystyle \ operatorname {tr} ^ {2} {\ mathfrak {H}} = \ operatorname {tr} ^ {2} {\ mathfrak {H}} '.}

Przekształcenia paraboliczne

Transformacja Möbiusa bez tożsamości zdefiniowana przez macierz determinanty jest

uważana za paraboliczną, jeśli

{\ Displaystyle {\ mathfrak {H}}}

{\ Displaystyle \ operatorname {tr} ^ {2} {\ mathfrak {H}} = (a + d) ^ {2} = 4}

(więc ślad jest plus lub minus 2; albo może wystąpić dla danej transformacji, ponieważ jest określany tylko do znaku). W rzeczywistości jeden z wyborów dla ma taki sam charakterystyczny wielomian X ² -2 X +1 jak macierz jednostkowa, a zatem jest unipotencjalny . Przekształcenie Möbiusa jest paraboliczne wtedy i tylko wtedy, gdy ma dokładnie jeden stały punkt w rozszerzonej płaszczyźnie zespolonej , co dzieje się wtedy i tylko wtedy, gdy można go zdefiniować za pomocą sprzężonej macierzy do

{\ Displaystyle {\ mathfrak {H}}}

{\ Displaystyle {\ mathfrak {H}}}

{\ Displaystyle {\ widehat {\ mathbb {C}}} = \ mathbb {C} \ filiżanka \ {\ infty \}}

{\ Displaystyle {\ zacząć {pmatrix} 1 i 1 \ \ 0 i 1 \ koniec {pmatrix}}}

który opisuje translację na płaszczyźnie zespolonej.

Zbiór wszystkich parabolicznych przekształceń Möbiusa o danym punkcie stałym w , wraz z tożsamością tworzy podgrupę izomorficzną z grupą macierzy ${\widehat {\mathbb {C}}}$

{\ Displaystyle \ lewo \ {{\ zacząć {pmatrix} 1 i b \ \ 0 i 1 \ koniec {pmatrix}} \ mid b \ w \ mathbb {C} \ po prawej \};}

jest to przykład z unipotentne rodnik o podgrupy Borel (grupy Mobius lub SL (2 C ) dla grupy matrycy; pojęcie to zdefiniowano dla dowolnego redukcyjnego grupy Lie ).

Stała charakterystyczna

Wszystkie transformacje nieparaboliczne mają dwa stałe punkty i są zdefiniowane przez sprzężenie macierzy do

{\ Displaystyle {\ zacząć {pmatrix} \ lambda i 0 \ \ 0 i \ lambda ^ {-1} \ koniec {pmatrix}}}

o liczbie zespolonej λ nie równej 0, 1 lub -1, odpowiadającej rozszerzeniu/obrótowi przez pomnożenie przez liczbę zespoloną k = λ ² , zwaną stałą charakterystyczną lub mnożnikiem transformacji.

Przekształcenia eliptyczne

Wykres Smith , stosowane przez elektryków do analizy linii przesyłowych , jest przedstawiony na eliptycznej Möbius transformacji y = (Z-1) / (Z + 1). Każdy punkt na wykresie Smitha reprezentuje jednocześnie zarówno wartość z (dolny lewy), jak i odpowiadającą mu wartość Γ (dolny prawy), dla |Γ |<1.

Mówi się, że transformacja jest eliptyczna, jeśli może być reprezentowana przez macierz, której ślad jest rzeczywisty z ${\ Displaystyle {\ mathfrak {H}}}$

{\ Displaystyle 0 \ leq \ operatorname {tr} ^ {2} {\ mathfrak {H}} <4.}

Przekształcenie jest eliptyczne wtedy i tylko wtedy, gdy | λ | = 1 i λ ≠ ±1. Pisząc , transformacja eliptyczna jest sprzężona z ${\ Displaystyle \ lambda = e ^ {i \ alfa}}$

{\ Displaystyle {\ zacząć {pmatrix} \ cos \ alfa & - \ sin \ alfa \ \ \ sin \ alfa i \ cos \ alfa \ koniec {pmatrix}}}

z α rzeczywistym.

Zauważ, że dla dowolnego ze stałą charakterystyczną k , stała charakterystyczna wynosi k ⁿ . Zatem wszystkie transformacje Möbiusa rzędu skończonego są transformacjami eliptycznymi, a mianowicie dokładnie tymi, w których λ jest pierwiastkiem jedności , lub równoważnie, gdzie α jest wymierną wielokrotnością $π$ . Najprostsza możliwość ułamkowej wielokrotności średniej α = $π$ /2, która jest również unikalnym przypadkiem , jest również oznaczona jako ${\ Displaystyle {\ mathfrak {H}}}$ ${\ Displaystyle {\ mathfrak {H}} ^ {n}}$ ${\ Displaystyle \ operatorname {tr} {\ mathfrak {H}} = 0}$ transformacja kołowa ; odpowiada to geometrycznie obrotowi o 180° wokół dwóch stałych punktów. Ta klasa jest reprezentowana w postaci macierzowej jako:

{\ Displaystyle {\ zacząć {pmatrix} 0 i 1 \ \ 1 i 0 \ koniec {pmatrix}}.}

Jest 3 przedstawicieli ustalających {0, 1, ∞}, które są trzema transpozycjami w grupie symetrii tych 3 punktów: który ustala 1 i zamienia 0 na ∞ (obrót o 180° wokół punktów 1 i −1), , który ustala ∞ i zamienia 0 na 1 (obrót o 180° wokół punktów 1/2 i ∞ ), a który ustala 0 i zamienia 1 na ∞ (obrót o 180° wokół punktów 0 i 2).

1/z

{\ Displaystyle 1-z}

{\ Displaystyle z/(z-1)}

Przekształcenia hiperboliczne

Mówi się, że transformata jest hiperboliczna, jeśli może być reprezentowana przez macierz, której ślad jest

rzeczywisty z

{\ Displaystyle {\ mathfrak {H}}}

{\ Displaystyle \ operatorname {tr} ^ {2} {\ mathfrak {H}}> 4.}

Przekształcenie jest hiperboliczne wtedy i tylko wtedy, gdy λ jest rzeczywiste i λ ≠ ±1.

Przekształcenia loksodromiczne

Mówi się, że transformata jest loksodromiczna, jeśli nie ma jej w [0,4]. Transformacja jest loksodromiczna wtedy i tylko wtedy, gdy . ${\ Displaystyle \ operatorname {tr} ^ {2} {\ mathfrak {H}}}$ $|\lambda |\neq 1$

Historycznie nawigacji przez loxodrome lub rumbu linii dotyczy ścieżki stałego łożyska ; wynikowa ścieżka jest spiralą logarytmiczną , podobną kształtem do przekształceń płaszczyzny zespolonej, które tworzy loksodromiczna transformacja Möbiusa. Zobacz figury geometryczne poniżej.

Generalna klasyfikacja

Transformacja	Ślad do kwadratu	Mnożniki	Reprezentant klasy
Okólnik	σ = 0	k = −1	${\zacząć{pmatrix}i&0\\0&-i\koniec{pmatrix}}$	z ↦ - oo
Eliptyczny	0 ≤ σ < 4	\| k \| = 1 ${\ Displaystyle k = e ^ {\ pm ja \ theta} \ neq 1}$	${\ Displaystyle {\ zacząć {pmatrix} e ^ {i \ theta /2} i 0 \ \ 0 i e ^ {-i \ theta /2} \ koniec {pmatrix}}}$	z ↦ e ^{i θ} z
Paraboliczny	σ = 4	k = 1	${\ Displaystyle {\ zacząć {pmatrix} 1 & a \ \ 0 i 1 \ koniec {pmatrix}}}$	z ↦ z + a
Hiperboliczny	4 < σ < ∞	${\ Displaystyle k \ w \ mathbb {R} ^ {+}}$ ${\ Displaystyle k = e ^ {\ pm \ theta} \ neq 1}$	${\ Displaystyle {\ zacząć {pmatrix} e ^ {\ theta /2} i 0 \ \ 0 i e ^ {-\ theta /2} \ koniec {pmatrix}}}$	z ↦ e ^θ z
Loxodromic	σ ∈ C \ [0,4]	$\|k\|\neq 1$ ${\ Displaystyle k = \ lambda ^ {2} \ lambda ^ {-2}}$	${\ Displaystyle {\ zacząć {pmatrix} \ lambda i 0 \ \ 0 i \ lambda ^ {-1} \ koniec {pmatrix}}}$	z ↦ kz

Prawdziwy przypadek i uwaga dotycząca terminologii

Na liczbach rzeczywistych (jeśli współczynniki muszą być rzeczywiste), nie ma niehiperbolicznych przekształceń loksodromicznych, a klasyfikacja jest na eliptyczną, paraboliczną i hiperboliczną, tak jak w przypadku rzeczywistych stożków . Terminologia wynika z uznania połowy wartości bezwzględnej śladu, |tr|/2, za mimośród przekształcenia – podział przez 2 koryguje wymiar, więc tożsamość ma mimośród 1 (tr/ n jest czasem używany jako alternatywa dla śladu z tego powodu), a wartość bezwzględna koryguje się dla śladu zdefiniowanego tylko do współczynnika ±1 ze względu na pracę w PSL. Alternatywnie można użyć połowy śladu do kwadratu jako zastępstwa dla kwadratu mimośrodu, jak to zrobiono powyżej; te klasyfikacje (ale nie dokładne wartości mimośrodowości, ponieważ wartości kwadratowe i bezwzględne są różne) zgadzają się dla śladów rzeczywistych, ale nie dla śladów złożonych. Ta sama terminologia jest używana do klasyfikacji elementów SL(2, R ) (podwójna okładka), a analogiczne klasyfikacje są używane w innych miejscach. Przekształcenia loksodromiczne są zasadniczo złożonym zjawiskiem i odpowiadają złożonym mimośrodom.

Interpretacja geometryczna stałej charakterystycznej

Poniższy rysunek przedstawia (po transformacji stereograficznej ze sfery do płaszczyzny) dwa stałe punkty transformacji Möbiusa w przypadku nieparabolicznym:

Charakterystyczną stałą można wyrazić w postaci jej logarytmu :

{\ Displaystyle e ^ {\ rho + \ alfa i} = k.}

Wyrażona w ten sposób liczba rzeczywista ρ staje się współczynnikiem rozszerzenia. Wskazuje, jak odpychający jest punkt stały γ ₁ i jak atrakcyjny jest γ ₂ . Liczba rzeczywista α jest współczynnikiem obrotu, wskazującym, w jakim stopniu transformacja obraca płaszczyznę w kierunku przeciwnym do ruchu wskazówek zegara o γ ₁ i zgodnie z ruchem wskazówek zegara o γ ₂ .

Transformacje eliptyczne

Jeśli ρ = 0, to punkty stałe nie są ani atrakcyjne, ani odpychające, ale obojętne, a transformacja jest eliptyczna . Te przekształcenia mają tendencję do przesuwania wszystkich punktów po okręgach wokół dwóch stałych punktów. Jeśli jeden ze stałych punktów znajduje się w nieskończoności, jest to równoznaczne z wykonaniem afinicznej rotacji wokół punktu.

Jeśli weźmiemy podgrupę jednoparametrową generowaną przez dowolną eliptyczną transformację Möbiusa, otrzymamy transformację ciągłą, taką, że każda transformacja w podgrupie ustala te same dwa punkty. Wszystkie inne punkty płyną wzdłuż rodziny okręgów, która jest zagnieżdżona pomiędzy dwoma stałymi punktami na sferze Riemanna. Ogólnie rzecz biorąc, dwa punkty stałe mogą być dowolnymi dwoma różnymi punktami.

Ma to ważną interpretację fizyczną. Wyobraź sobie, że jakiś obserwator obraca się ze stałą prędkością kątową wokół pewnej osi. Następnie możemy przyjąć dwa stałe punkty za bieguny północny i południowy sfery niebieskiej. Wygląd nocnego nieba jest teraz przekształcany w sposób ciągły dokładnie w sposób opisany przez jednoparametrową podgrupę przekształceń eliptycznych dzielących punkty stałe 0, ∞ oraz o liczbie α odpowiadającej stałej prędkości kątowej naszego obserwatora.

Oto kilka figur ilustrujących wpływ eliptycznej transformacji Möbiusa na sferę Riemanna (po rzucie stereograficznym na płaszczyznę):

Te zdjęcia ilustrują efekt pojedynczej transformacji Möbiusa. Podgrupa jednoparametrowa, którą generuje w sposób ciągły przesuwa punkty wzdłuż rodziny łuków kołowych sugerowanych na obrazach.

Transformacje hiperboliczne

Jeśli α wynosi zero (lub wielokrotność 2 $π$ ), wtedy mówimy, że transformacja jest hiperboliczna . Te przekształcenia mają tendencję do przesuwania punktów po kołowych ścieżkach od jednego stałego punktu do drugiego.

Jeśli weźmiemy podgrupę jednoparametrową wygenerowaną przez dowolną hiperboliczną transformację Möbiusa, otrzymamy transformację ciągłą, taką, że każda transformacja w podgrupie ustala te same dwa punkty. Wszystkie inne punkty przepływać wzdłuż pewnej rodziny łuków kołowych z dala od pierwszego stałego punktu i kierunku drugiego punktu stałego. Ogólnie rzecz biorąc, dwa punkty stałe mogą być dowolnymi dwoma różnymi punktami na sferze Riemanna.

To również ma ważną fizyczną interpretację. Wyobraź sobie, że obserwator przyspiesza (ze stałą wartością przyspieszenia) w kierunku bieguna północnego na swojej sferze niebieskiej. Następnie wygląd nocnego nieba jest przekształcany dokładnie w sposób opisany przez jednoparametrową podgrupę przekształceń hiperbolicznych dzielących punkty stałe 0, ∞, z liczbą rzeczywistą ρ odpowiadającą wielkości jego wektora przyspieszenia. Gwiazdy wydają się poruszać wzdłuż długości geograficznej, od bieguna południowego do bieguna północnego. (Długości geograficzne są wyświetlane jako okrągłe łuki w rzucie stereograficznym ze sfery na płaszczyznę.)

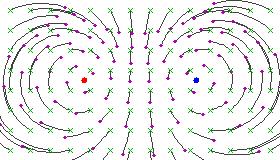
Oto kilka rysunków ilustrujących wpływ hiperbolicznej transformacji Möbiusa na sferę Riemanna (po stereograficznym rzucie na płaszczyznę):

Obrazy te przypominają linie pola dodatniego i ujemnego ładunku elektrycznego znajdujące się w stałych punktach, ponieważ kołowe linie przepływu tworzą stały kąt między dwoma stałymi punktami.

Przekształcenia loksodromiczne

Jeśli zarówno ρ, jak i α są niezerowe, wtedy mówi się, że transformacja jest loksodromiczna . Te przekształcenia mają tendencję do przenoszenia wszystkich punktów na ścieżkach w kształcie litery S z jednego stałego punktu do drugiego.

Słowo „ loxodrom ” pochodzi z greckiego: „λοξος (loxos), skośny + δρόμος (dromos), oczywiście ”. Podczas żeglowania na stałym łożysku - jeśli zachować nagłówek (powiedzmy) północno-wschodniej, będzie ostatecznie skończyć żeglować wokół bieguna północnego w spirali logarytmicznej . Na rzucie merkatora taki kurs jest linią prostą, ponieważ bieguny północny i południowy rzutują w nieskończoność. Kąt, że leży naprzeciwko loxodrome względem długości linii (czyli jego nachylenie, w „szczelność” spirali) jest argumentem k . Oczywiście transformacje Möbiusa mogą mieć swoje dwa stałe punkty w dowolnym miejscu, nie tylko na biegunach północnym i południowym. Ale każda transformacja lokodromiczna będzie sprzężona z transformacją, która przesuwa wszystkie punkty wzdłuż takich loksodromów.

Jeśli weźmiemy podgrupę jednoparametrową generowaną przez dowolną loksodromiczną transformację Möbiusa, otrzymamy transformację ciągłą, taką, że każda transformacja w podgrupie ustala te same dwa punkty. Wszystkie inne punkty przepływać wzdłuż pewnej rodziny krzywych, z dala od pierwszego stałego punktu i kierunku drugiego punktu stałego. W przeciwieństwie do przypadku hiperbolicznego, te krzywe nie są kołowymi łukami, ale pewnymi krzywymi, które w projekcji stereograficznej z kuli na płaszczyznę wyglądają jak krzywe spiralne, które skręcają się w kierunku przeciwnym do ruchu wskazówek zegara nieskończenie często wokół jednego stałego punktu i nieskończenie często skręcają się zgodnie z ruchem wskazówek zegara wokół drugiego stałego punktu. Ogólnie rzecz biorąc, dwa punkty stałe mogą być dowolnymi dwoma różnymi punktami na sferze Riemanna.

Prawdopodobnie można się domyślać interpretacji fizycznej w przypadku, gdy dwa stałe punkty wynoszą 0, ∞: obserwator, który obraca się (ze stałą prędkością kątową) wokół jakiejś osi i porusza się wzdłuż tej samej osi, zobaczy nocne niebo transformację zgodnie z jednoparametrową podgrupą przekształceń loksodromicznych z punktami stałymi 0, ∞ oraz z ρ, α określonymi odpowiednio przez wielkość rzeczywistych prędkości liniowych i kątowych.

Projekcja stereograficzna

Obrazy te pokazują transformacje Möbiusa rzutowane stereograficznie na sferę Riemanna . Zauważ w szczególności, że kiedy jest rzutowany na kulę, szczególny przypadek stałego punktu w nieskończoności nie różni się niczym od posiadania stałych punktów w dowolnym miejscu.

Jeden stały punkt w nieskończoności
Eliptyczny	Hiperboliczny	Loxodromic
Punkty stałe po przekątnej po przeciwnej stronie
Eliptyczny	Hiperboliczny	Loxodromic
Punkty stałe w dowolnej lokalizacji
Eliptyczny	Hiperboliczny	Loxodromic

Iteracja transformacji

Jeśli transformacja ma punkty stałe γ

₁ , γ ₂ , i stałą charakterystyczną k , to będzie miała .

{\ Displaystyle {\ mathfrak {H}}}

{\ Displaystyle {\ mathfrak {H}} '= {\ mathfrak {H}} ^ {n}}

{\ Displaystyle \ gamma _ {1} '= \ gamma _ {1} \ gamma _ {2} ' = \ gamma _ {2} k' = k ^ {n}}

Można to wykorzystać do iteracji transformacji lub do animowania jej poprzez rozbicie jej na etapy.

Obrazy te pokazują trzy punkty (czerwony, niebieski i czarny) powtarzane w sposób ciągły w wyniku przekształceń z różnymi charakterystycznymi stałymi.

A te obrazy pokazują, co się dzieje, gdy przekształcasz okrąg w przekształceniach hiperbolicznych, eliptycznych i loksodromicznych. Zauważ, że na obrazach eliptycznych i loksodromicznych wartość α wynosi 1/10 .

Wyższe wymiary

W większych wymiarach, A funkcja homograficzna jest homeomorfizm z The

punktowe zwartym z , który jest ograniczony skład inwersji w dziedzinach i odbicia w hiperplaszczyzn . Twierdzenie Liouville'a w geometrii konforemnej mówi, że w wymiarze co najmniej trzecim wszystkie przekształcenia konforemne są przekształceniami Möbiusa. Każdą transformację Möbiusa można umieścić w formie

{\ Displaystyle {\ overline {\ mathbb {R} ^ {n}}}}

{\ Displaystyle \ mathbb {R} ^ {n}}

{\ Displaystyle f (x) = b + {\ Frac {\ alfa A (xa)} {| xa | ^ {\ varepsilon}}}}

gdzie , , jest

macierzą ortogonalną i wynosi 0 lub 2. Grupa przekształceń Möbiusa jest również nazywana grupą Möbiusa .

{\ Displaystyle a, b \ w \ mathbb {R} ^ {n}}

{\ Displaystyle \ alfa \ w \ mathbb {R}}

{\ Displaystyle A}

\varepsilon

Przekształcenia Möbiusa zachowujące orientację tworzą połączony składnik tożsamości w grupie Möbiusa. W wymiarze n = 2 transformacje Möbiusa zachowujące orientację są dokładnie mapami sfery Riemanna omówionej tutaj. Te odwracające orientację uzyskuje się z nich w wyniku złożonej koniugacji.

Domena transformacji Möbiusa, tj. , jest homeomorficzna z

n- wymiarową sferą . Kanoniczny izomorfizm między tymi dwiema przestrzeniami to transformata Cayleya , która sama jest transformacją Möbiusa . Ta identyfikacja oznacza, że transformacje Möbiusa można również traktować jako konformalne izomorfizmy . N -sphere wraz z działaniem grupy Möbius jest struktura geometryczna (w sensie Kleina programu Erlangen ) o nazwie Möbiusa geometrii .

{\ Displaystyle {\ overline {\ mathbb {R} ^ {n}}}}

{\ Displaystyle S ^ {n}}

{\ Displaystyle {\ overline {\ mathbb {R} ^ {n + 1}}}}

{\ Displaystyle S ^ {n}}

Aplikacje

Transformacja Lorentza

Kilku autorów odnotowało izomorfizm grupy Möbiusa z grupą Lorentza : Na podstawie wcześniejszej pracy Felixa Kleina (1893, 1897) na temat funkcji automorficznych związanych z geometrią hiperboliczną i geometrią Möbiusa, Gustav Herglotz (1909) wykazał, że ruchy hiperboliczne (tj. izometryczne automorfizmy o hiperbolicznej przestrzeni ) transformację sfery jednostkowej w sobie odpowiadają transformacji Lorentza, w którym Herglotz był zdolny do klasyfikowania jednego parametru Lorentza transformacji w loxodromic, eliptyczny, hiperbolicznych i grupy parabolicznych. Inni autorzy to Emil Artin (1957), HSM Coxeter (1965) i Roger Penrose , Wolfgang Rindler (1984), Tristan Needham (1997) i WM Olivia (2002).

Przestrzeń Minkowskiego składa się z czterowymiarowej przestrzeni współrzędnych rzeczywistych R ⁴ składającej się z przestrzeni uporządkowanych czwórek ( x ₀ , x ₁ , x ₂ , x ₃ ) liczb rzeczywistych wraz z formą kwadratową

{\ Displaystyle Q (x_{0},x_{1},x_{2},x_{3})=x_{0}^{2}-x_{1}^{2}-x_{2}^{ 2}-x_{3}^{2}.}

Zapożyczając terminologię ze szczególnej teorii względności , punkty z $Q > 0$ są uważane za podobne do czasu ; ponadto, jeśli $x 0 > 0$ , to punkt nazywamy wskazywaniem przyszłości . Punkty z $Q < 0$ nazywane są przestrzenią . Zerowy stożka S składa się z tych punktach, w których $Q = 0$ ; przyszłości zerowy stożka N ⁺ są te punkty zerowy stożek $x 0 > 0$ . Niebieskich kula jest następnie identyfikowany z kolekcji promieni w N ⁺ , którego punkt początkowy znajduje się źródłem R ⁴ . Zbiór przekształceń liniowych na R ⁴ z dodatnim wyznacznikiem z zachowaniem kwadratowej postaci Q i zachowaniem kierunku czasu z ograniczonej grupy Lorentza SO ⁺ (1,3).

W związku z geometrią sfery niebieskiej grupę przekształceń SO ⁺ (1,3) utożsamia się z grupą przekształceń sfery PSL(2, C ) Möbiusa. Do każdego $(x 0, x 1, x 2, x 3) \in R 4$ , skojarz macierz hermitowską

{\ Displaystyle X = {\ zacząć {bmatrix} x_ {0}+ x_ {1} i x_ {2} + ix_ {3} \ \ x_ {2}-ix_ {3} i x_ {0}-x_ {1} \ koniec{bmatrix}}.}

Wyznacznikiem macierzy X jest równe $P (x 0, x 1, x 2, x 3)$ . Specjalną grupę liniowy działa na powierzchni takich matryc poprzez

{\ Displaystyle X \ mapsto AXA ^ {*}}

( 1 )

dla każdego A ∈ SL(2, C ), a to działanie SL(2, C ) zachowuje wyznacznik X, ponieważ $det A = 1$ . Ponieważ wyznacznik X jest utożsamiany z kwadratową postacią Q , SL(2, C ) działa przez transformacje Lorentza. Ze względów wymiarowych SL(2, C ) obejmuje sąsiedztwo identyczności SO(1,3). Ponieważ SL(2, C ) jest połączony, obejmuje całą ograniczoną grupę Lorentza SO ⁺ (1,3). Ponadto, ponieważ jądrem działania ( 1 ) jest podgrupa {± I }, to przejście do grupy ilorazowej daje izomorfizm grupy

{\ Displaystyle \ operatorname {PSL} (2 \ mathbb {C}) \ cong \ operatorname {SO} ^ {+} (1,3).}

( 2 )

Skupiając teraz uwagę na przypadku, gdy ( x ₀ , x ₁ , x ₂ , x ₃ ) ma wartość null, macierz X ma wyznacznik zerowy, a zatem dzieli się jako produkt zewnętrzny złożonego dwuwektorowego ξ z jego sprzężeniem zespolonym:

{\ Displaystyle X = \ xi {\ bar {\ xi}} ^ {T} = \ xi \ xi ^ {*}.}

( 3 )

Na wektor dwuskładnikowy ξ oddziałuje SL(2, C ) w sposób zgodny z ( 1 ). Teraz jest jasne, że jądro reprezentacji SL(2, C ) na macierzach hermitowskich to {± I }.

Działanie PSL(2, C ) na sferę niebieską można również opisać geometrycznie za pomocą projekcji stereograficznej . Rozważmy najpierw hiperpłaszczyznę w R ⁴ podaną przez x ₀ = 1. Sferę niebieską można utożsamić ze sferą S ⁺ przecięcia hiperpłaszczyzny z przyszłym stożkiem zerowym N ⁺ . Rzut stereograficzny z bieguna północnego (1,0,0,1) tej kuli na płaszczyznę x ₃ = 0 przyjmuje punkt o współrzędnych (1, x ₁ , x ₂ , x ₃ ) o

x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=1

do momentu

{\ Displaystyle \ lewo (1, {\ Frac {x_ {1}} {1-x_ {3}}}, {\ Frac {x_ {2}} {1-x_ {3}}}, 0 \ po prawej) .}

Przedstawiamy złożoną współrzędną

{\ Displaystyle \ zeta = {\ Frac {x_ {1}+ ix_ {2}}{1-x_ {3}}},}

odwrotna projekcja stereograficzna daje następujący wzór na punkt ( x ₁ , x ₂ , x ₃ ) na S ⁺ :

{\ Displaystyle {\ zacząć {wyrównany} x_ {1} i = {\ Frac {\ zeta + {\ bar {\ zeta}}} {\ zeta {\ bar {\ zeta}} + 1}} \ \ x_ { 2}&={\frac {\zeta -{\bar {\zeta }}}{i(\zeta {\bar {\zeta }}+1)}}\\x_{3}&={\frac { \zeta {\bar {\zeta }}-1}{\zeta {\bar {\zeta }}+1}}.\end{wyrównany}}}

( 4 )

Działanie SO ⁺ (1,3) na punkty N ⁺ nie zachowuje hiperpłaszczyzny S ⁺ , ale działanie na punkty w S ⁺ a następnie przeskalowanie tak, że wynik jest ponownie w S ⁺ daje działanie SO ⁺ ( 1,3) na sferze, która przechodzi do działania na zmienną zespoloną ζ. W rzeczywistości to działanie polega na ułamkowych przekształceniach liniowych, chociaż nie jest to łatwo widoczne z tej reprezentacji sfery niebieskiej. I odwrotnie, dla każdej ułamkowej transformacji liniowej ζ zmienna przechodzi do unikalnej transformacji Lorentza na N ⁺ , prawdopodobnie po odpowiednim (jednoznacznie określonym) przeskalowaniu.

Bardziej niezmiennym opisem rzutu stereograficznego, który pozwala na wyraźniejsze uwidocznienie działania, jest rozważenie zmiennej ζ = z : w jako stosunku pary jednorodnych współrzędnych dla złożonej linii rzutowej CP ¹ . Rzut stereograficzny przechodzi do przekształcenia od C ² − {0} do N ^+, które jest jednorodne stopnia drugiego względem skalowania rzeczywistego

{\ Displaystyle (z, w) \ mapsto (x_ {0}, x_ {1}, x_ {2}, x_ {3}) = (z {\ bar {z}} + w {\ bar {w}} ,z{\bar {z}}-w{\bar {w}},z{\bar {w}}+w{\bar {z}},i^{-1}(z{\bar {w }}-w{\bar {z}}))}

( 5 )

co zgadza się z ( 4 ) po ograniczeniu do skali, w której Składniki (

5 ) są dokładnie tymi uzyskanymi z produktu zewnętrznego

{\ Displaystyle Z {\ bar {z}} + w {\ bar {w}} = 1.}

{\rozpocznij {bmatrix}x_{0}+x_{1}&x_{2}+ix_{3}\\x_{2}-ix_{3}&x_{0}-x_{1}\end{ bmatrix}}=2{\begin{bmatrix}z\\w\end{bmatrix}}{\begin{bmatrix}{\bar {z}}&{\bar {w}}\end{bmatrix}}.

Podsumowując, działanie ograniczonej grupy Lorentza SO ⁺ (1,3) zgadza się z działaniem grupy Möbiusa PSL(2, C ). To uzasadnia następującą definicję. W wymiarze n ≥ 2, grupa Möbiusa Möb( n ) jest grupą wszystkich

izometrii konforemnych sfery okrągłej S ⁿ zachowujących orientację względem siebie. Realizując sferę konforemną jako przestrzeń skierowanych w przyszłość promieni stożka zerowego w przestrzeni Minkowskiego R ^1,n+1 , istnieje izomorfizm Möb( n ) z ograniczoną grupą Lorentza SO ⁺ (1, n +1 ) przekształceń Lorentza z dodatnim wyznacznikiem, z zachowaniem kierunku czasu.

Coxeter zaczął zamiast tego od równoważnej formy kwadratowej ${\ Displaystyle Q (x_ {1}, \ x_ {2}, \ x_ {3} \ x_ {4}) = x_ {1} ^ {2} + x_ {2} ^ {2} + x_ {3} ^{2}-x_{4}^{2}.}$

Zidentyfikował grupę Lorentza z przekształceniami, dla których { x :Q( x )=-1} jest stabilne . Następnie zinterpretował x jako jednorodne współrzędne i { x : Q( x ) = 0}, stożek zerowy , jako absolut Cayleya dla hiperbolicznej przestrzeni punktów { x : Q( x ) < 0}. Następnie Coxeter przedstawił zmienne

{\ Displaystyle \ xi = {\ Frac {x_ {1}} {x_ {4}}} \ \ eta = {\ Frac {x_ {2}} {x_ {4}}} \ \ zeta = {\ szczelina {x_{3}}{x_{4}}}}

tak, że kwadryka niezmiennika Lorentza odpowiada sferze Coxeter zauważa, że

Felix Klein również pisał o tej korespondencji, stosując rzut stereograficzny z (0, 0, 1) na płaszczyznę zespoloną Coxeter wykorzystał fakt, że koła płaszczyzny odwrotnej reprezentują płaszczyzny przestrzeń hiperboliczna, a ogólna homografia jest iloczynem inwersji w dwóch lub czterech okręgach, co odpowiada ogólnemu przemieszczeniu hiperbolicznemu, które jest iloczynem inwersji w dwóch lub czterech płaszczyznach.

{\ Displaystyle \ xi ^ {2} + \ eta ^ {2} + \ zeta ^ {2} = 1.}

{\textstyle z={\frac {\xi +i\eta }{1-\zeta }}.}

Przestrzeń hiperboliczna

Jak widać powyżej, grupa Möbiusa PSL(2, C ) działa w przestrzeni Minkowskiego jako grupa tych izometrii, które zachowują pochodzenie, orientację przestrzeni i kierunek czasu. Ograniczając się do punktów, w których Q =1 w dodatnim stożku świetlnym, które tworzą model hiperbolicznej 3-przestrzeni H ³ , widzimy, że grupa Möbiusa działa na H ³ jako grupa izometrii zachowujących orientację. W rzeczywistości grupa Möbiusa jest równa grupie zachowujących orientację izometrii hiperbolicznej 3-przestrzeni.

Jeśli użyjemy modelu kulki Poincaré , identyfikując kulę jednostkową w R ³ z H ³ , możemy myśleć o sferze Riemanna jako o "konformalnej granicy" H ³ . Każda izometria H ³ zachowująca orientację daje początek transformacji Möbiusa na sferze Riemanna i odwrotnie; jest to pierwsza obserwacja prowadząca do przypuszczeń dotyczących korespondencji AdS/CFT w fizyce.

Zobacz też

Uwagi

Bibliografia

Konkretny

Ogólny

Arnold, Douglas N.; Rogness, Jonathan (2008), "Möbius Transformations Revealed" (PDF) , Zawiadomienia o AMS , 55 (10): 1226-1231
Beardon, Alan F. (1995), Geometria grup dyskretnych , New York: Springer-Verlag, ISBN 978-0-387-90788-8
Hall, GS (2004), Symetrie i struktura krzywizny w ogólnej teorii względności , Singapur: World Scientific, ISBN 978-981-02-1051-9 (Patrz rozdział 6, aby zapoznać się z klasyfikacją, aż do sprzężenia, podalgebr Liego z algebry Liego grupy Lorentza).
Katok, Svetlana (1992), Fuchsian Groups , Chicago: University of Chicago Press, ISBN 978-0-226-42583-2 Zobacz rozdział 2 .
Klein Felix (1888), Wykłady na dwudziestościan i rozwiązywanie równań piątego stopnia (Dover ed.), ISBN 978-0-486-49528-6.
Knopp, Konrad (1952), Elementy teorii funkcji , New York: Dover, ISBN 978-0-486-60154-0 (Patrz rozdziały 3–5 tej klasycznej książki, aby uzyskać piękne wprowadzenie do sfery Riemanna, projekcji stereograficznej i transformacji Möbiusa.)
Mumford, Dawid ; Seria, Karolina; Wright, David (2002), Perły Indry: Wizja Felixa Kleina , Cambridge University Press, ISBN 978-0-521-35253-6 (Skierowany do niematematyków, zapewnia doskonałą ekspozycję teorii i wyników, bogato ilustrowaną diagramami.)
Needham, Tristan (1997), Wizualna Analiza Złożona , Oxford: Clarendon Press, ISBN 978-0-19-853446-4 (Patrz rozdział 3, aby uzyskać pięknie zilustrowane wprowadzenie do transformacji Möbiusa, w tym ich klasyfikację aż do sprzężenia.)
Penrose'a, Rogera ; Rindler, Wolfgang (1984), Spinors i czasoprzestrzeń , tom 1: Rachunek z dwoma spinorami i pola relatywistyczne , Cambridge University Press, ISBN 978-0-521-24527-2
Schwerdtfeger, Hans (1979), Geometria liczb zespolonych , Dover, ISBN 978-0-486-63830-0 (Patrz rozdział 2, aby zapoznać się z wprowadzeniem do transformacji Möbiusa.)
Tóth, Gábor (2002), skończone grupy Möbiusa, minimalne zanurzenia sfer i moduły

Dalsza lektura

Lawson, MV (1998). „Odwrócony monoid Möbiusa” . Dziennik Algebry . 200 (2): 428. doi : 10.1006/jabr.1997.7242 .

Zewnętrzne linki

Multimedia związane z transformacją Möbiusa w Wikimedia Commons
„Quasi-konformalne mapowanie” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
Galeria map konformalnych
Weisstein, Eric W. „Liniowa transformacja ułamkowa” . MatematykaŚwiat .

Languages

In other projects

Transformacja Möbiusa - Möbius transformation

Przegląd

Definicja

Punkty stałe

Wyznaczanie punktów stałych

Dowód topologiczny

Forma normalna

Polacy transformacji

Proste przekształcenia i kompozycja Möbiusa

Kompozycja prostych przekształceń

Podstawowe właściwości

Wzór na odwrotną transformację

Zachowanie kątów i uogólnionych okręgów

Zachowanie współczynnika krzyżowego

Koniugacja

Reprezentacje macierzy projekcyjnej

Określanie przekształcenia przez trzy punkty

Mapowanie najpierw do 0, 1, ∞

Wyraźna formuła wyznacznika

Podgrupy grupy Möbius

Klasyfikacja

Przekształcenia paraboliczne

Stała charakterystyczna

Przekształcenia eliptyczne

Przekształcenia hiperboliczne

Przekształcenia loksodromiczne

Generalna klasyfikacja

Prawdziwy przypadek i uwaga dotycząca terminologii

Interpretacja geometryczna stałej charakterystycznej

Transformacje eliptyczne

Transformacje hiperboliczne

Przekształcenia loksodromiczne

Projekcja stereograficzna

Iteracja transformacji

Wyższe wymiary

Aplikacje

Transformacja Lorentza

Przestrzeń hiperboliczna

Zobacz też

Uwagi

Bibliografia

Dalsza lektura

Zewnętrzne linki