Wyznacznik - Determinant

W matematyce The determinantą jest wartością skalarną , która to funkcja z wpisów w macierzy kwadratowej . Pozwala scharakteryzować niektóre właściwości macierzy i odwzorowania liniowego reprezentowanego przez macierz. W szczególności wyznacznik jest niezerowy wtedy i tylko wtedy, gdy macierz jest odwracalna, a odwzorowanie liniowe reprezentowane przez macierz jest izomorfizmem . Wyznacznik iloczynu macierzy jest iloczynem ich wyznaczników (poprzednia własność jest następstwem tej). Wyznacznik macierzy A oznaczamy det( A ) , det A lub | | .

W przypadku macierzy 2 × 2 wyznacznik można zdefiniować jako

${\ Displaystyle {\ zacznij {wyrównany} | A | = {\ zacznij {vmatrix} a & b \ \ c i d \ koniec {vmatrix}} = ad-BC. \ koniec {wyrównany}}}$

Podobnie, dla macierzy 3 × 3 A , jej wyznacznikiem jest

${\ Displaystyle {\ zacznij {wyrównany} | A | = {\ zacznij {vmatrix} a&b&c\\d&e&f\\g&h&i\end {vmatrix}}}&=a\,{\zacznij {vmatrix}e&f\\h&i\end{ vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&= aei+bfg+cdh-ceg-bdi-afh.\end{wyrównany}}}$

Każdy wyznacznik macierzy 2 × 2 w tym równaniu nazywa się podrzędną macierzy A . Ta procedura może zostać rozszerzona, aby dać rekurencyjną definicję wyznacznika macierzy n × n , znaną jako rozwinięcie Laplace'a .

Wyznaczniki występują w całej matematyce. Na przykład macierz jest często używana do reprezentowania współczynników w układzie równań liniowych , a wyznaczniki mogą być używane do rozwiązywania tych równań ( reguła Cramera ), chociaż inne metody rozwiązywania są znacznie bardziej wydajne obliczeniowo. Wyznaczniki służą do definiowania charakterystycznego wielomianu macierzy, którego pierwiastkami są wartości własne . W geometrii , podpisany n wymiarową objętość z n -wymiarowej równoległościanu wyraża determinantę. Jest to wykorzystywane w rachunku różniczkowym z zewnętrznymi formami różniczkowymi i wyznacznikiem jakobianu , w szczególności do zmian zmiennych w całkach wielokrotnych .

2 × 2 macierze

Wyznacznik matrycy 2 × 2 jest oznaczony jako „det” lub pionowymi paskami wokół matrycy i jest zdefiniowany jako ${\displaystyle {\zacząć{pmatrix}a&b\\c&d\koniec{pmatrix}}}$

${\displaystyle \operatorname {det} {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\rozpocznij {vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.}$

Na przykład,

${\ Displaystyle \ Operatorname {det} {\ zacząć {pmatrix} 3 i 7 \ \ 1 i 4 \ koniec {pmatrix}} = {\ zacząć {vmatrix} 3 i 7 \ \ 1 i {-4} \ koniec {vmatrix}}} = 3 \ cdot (-4)-7\cdot 1=-19.}$

Pierwsze właściwości

Wyznacznik ma kilka kluczowych właściwości, które można udowodnić przez bezpośrednią ocenę definicji macierzy -, i które nadal obowiązują dla wyznaczników większych macierzy. Są one następujące: po pierwsze, wyznacznikiem macierzy jednostkowej jest 1. Po drugie, wyznacznikiem jest zero, jeśli dwa wiersze są takie same: ${\displaystyle 2\razy 2}$ ${\ Displaystyle {\ zacząć {pmatrix} 1 i 0 \ \ 0 i 1 \ koniec {pmatrix}}}$

${\displaystyle {\zaczynać{vmatrix}a&b\\a&b\koniec {vmatrix}}=ab-ba=0.}$

Podobnie jest, jeśli dwie kolumny są takie same. Ponadto,

${\ Displaystyle {\ zacząć {vmatrix} a & b + b '\ \ c & d + d' \ koniec {vmatrix}} = a (d + d ') - (b + b ') c = {\ zacząć {vmatrix} a & b\ \c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.}$

Wreszcie, jeśli jakakolwiek kolumna jest pomnożona przez pewną liczbę (tj. wszystkie wpisy w tej kolumnie są pomnożone przez tę liczbę), wyznacznik jest również mnożony przez tę liczbę: ${\ Displaystyle r}$

${\ Displaystyle {\ zacząć {vmatrix} r \ cdot a&b\\r\cdot c&d\koniec {vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\zacząć {vmatrix}a&b\\c&d \end{vmatrix}}.}$

Znaczenie geometryczne

Jeśli wpisy macierzy są liczbami rzeczywistymi, macierz A może być użyta do reprezentowania dwóch odwzorowań liniowych : jednej, która odwzorowuje standardowe wektory bazowe na wiersze A , i drugiej, która odwzorowuje je na kolumny A . W obu przypadkach obrazy wektorów bazowych tworzą równoległobok, który reprezentuje obraz kwadratu jednostkowego pod mapowaniem. Równoległobok określone przez rzędy powyższej macierzy jest jednym z wierzchołków w (0, 0) , ( , b ) , ( + c , b + d ) , i ( c , d ) , jak pokazano na załączonym diagram.

Wartość bezwzględna ad − bc jest polem równoległoboku, a zatem reprezentuje współczynnik skali, o który pola są przekształcane przez A . (Równoległobok utworzony przez kolumny A jest ogólnie innym równoległobokiem, ale ponieważ wyznacznik jest symetryczny względem rzędów i kolumn, obszar będzie taki sam.)

Wartość bezwzględna wyznacznika wraz ze znakiem staje się zorientowanym obszarem równoległoboku. Obszar zorientowany jest taki sam jak obszar zwykły , z tym wyjątkiem, że jest ujemny, gdy kąt od pierwszego do drugiego wektora definiującego równoległobok obraca się w kierunku zgodnym z ruchem wskazówek zegara (który jest przeciwny do kierunku, jaki uzyskano by dla macierzy jednostkowej ).

Aby pokazać, że ad − bc jest polem ze znakiem , można rozważyć macierz zawierającą dwa wektory u ≡ ( a , b ) i v ≡ ( c , d ) reprezentujące boki równoległoboku. Podpisany obszar można wyrazić jako | ty | | v | sin  θ dla kąta θ między wektorami, który jest po prostu podstawą razy wysokość, długość jednego wektora razy prostopadła składowa drugiego. Ze względu na sinus jest to już obszar ze znakiem , ale wygodniej można go wyrazić za pomocą cosinusa kąta komplementarnego do wektora prostopadłego, np. u ^⊥ = (− b , a ) , tak że | ty ^⊥ | | v | cos  θ′ , który można określić wzorem iloczynu skalarnego równym ad − bc :

${\ Displaystyle {\ tekst {podpisany obszar}} = | {\ pogrubienie {u}} | \, | {\ pogrubienie {v}} | \, \ grzech \ \ theta = \ lewo | {\ pogrubienie {u} }^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix} }\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.}$

Zatem wyznacznik podaje współczynnik skalowania i orientację wywołaną przez odwzorowanie reprezentowane przez A . Gdy wyznacznik jest równy jeden, odwzorowanie liniowe zdefiniowane przez macierz jest równopowierzchniowe i zachowuje orientację.

Obiekt znany jako dwuwektor jest powiązany z tymi pomysłami. 2D, może być interpretowane jako zorientowany segmentu płaszczyzny utworzonej przez wyobrazić sobie dwa wektory każdy z pochodzenia (0, 0) , i współrzędne ( , b ) i ( c , d ) . Wielkość dwuwektorowa (oznaczona przez ( a , b ) ∧ ( c , d ) ) to obszar znaku , który jest również wyznacznikiem ad − bc .

Jeśli n × n rzeczywista macierz A jest zapisana w postaci jej wektorów kolumnowych , to ${\ Displaystyle A = \ lewo [{\ zacząć {tablica} {c | c | c | c} \ mathbf {a} _ {1} i \ mathbf {a} _ {2} i \ cdots i \ mathbf {a } _{n}\end{array}}\right]}$

${\ Displaystyle A {\ zacząć {pmatrix} 1 \ \ 0 \ \ \ vdots \ \ 0 \ koniec {pmatrix}} = \ mathbf {a} _ {1}, \ quad A {\ zacząć {pmatrix} 0 \ \ 1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\vdots \\1 \end{pmatrix}}=\mathbf {a} _{n}.}$

Oznacza to, że odwzorowuje jednostkę n- sześcianu na n- wymiarowy równoległotop zdefiniowany przez wektory regionu${\ Displaystyle A}$${\ Displaystyle \ mathbf {a} _ {1}, \ mathbf {a} _ {2}, \ ldots, \ mathbf {a} _ {n},}$${\ Displaystyle P = \ lewo \ {c_ {1} \ mathbf {a} _ {1} + \ cdots + c_ {n} \ mathbf {a} _ {n} \ mid 0 \ równoważnik c_ {i} \ równoważnik 1\ \dla wszystkich\prawo\}.}$

Wyznacznik daje podpisany n wymiarową objętości tego parallelotope, a więc opisuje bardziej ogólnie, N -wymiarową współczynnika skalowania głośności na liniowej transformacji wytwarzanego przez A . (Znak pokazuje, czy transformacja zachowuje, czy odwraca orientację .) W szczególności, jeśli wyznacznikiem jest zero, to ten równoległobok ma objętość zero i nie jest w pełni n- wymiarowy, co wskazuje, że wymiar obrazu A jest mniejszy niż n . Oznacza to, że A wytwarza transformację liniową, która nie jest ani na, ani jeden do jednego , a więc nie jest odwracalna. ${\ Displaystyle \ det (A) = \ pm {\ tekst {objętość}} (P)}$

Definicja

W sequelu A jest kwadratową macierzą z n wierszami i n kolumnami, dzięki czemu można ją zapisać jako

${\ Displaystyle A = {\ zacząć {bmatrix} a_ {1,1} i a_ {1,2} i \ kropki i a_ {1, n} \ \ a_ {2,1} i a_ {2,2} i \ kropki i a_ {2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\dots &a_{n,n}\end{bmatrix}}.}$

Wpisy itp. są w wielu przypadkach liczbami rzeczywistymi lub zespolonymi. Jak omówiono poniżej, wyznacznik jest również zdefiniowany dla macierzy, których wpisy są elementami bardziej abstrakcyjnych struktur algebraicznych, znanych jako pierścienie przemienne . ${\ Displaystyle a_ {1,1}}$

Wyznacznik A jest oznaczany przez det( A ) lub może być oznaczony bezpośrednio w kategoriach wpisów macierzowych, pisząc zamknięte kreski zamiast nawiasów:

${\ Displaystyle {\ zacząć {vmatrix} a_ {1,1} i a_ {1,2} i \ kropki i a_ {1, n} \ \ a_ {2,1} i a_ {2,2} i \ kropki i a_ {2 ,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\dots &a_{n,n}\end{vmatrix}}.}$

Istnieją różne równoważne sposoby definiowania wyznacznika macierzy kwadratowej A , tj. o tej samej liczbie wierszy i kolumn: wyznacznik można zdefiniować za pomocą formuły Leibniza , wyraźnej formuły zawierającej sumy iloczynów niektórych wpisów macierzy. Wyznacznik można również scharakteryzować jako unikalną funkcję zależną od wpisów macierzy spełniających określone właściwości. Podejście to można również wykorzystać do obliczenia wyznaczników poprzez uproszczenie danych macierzy.

Wzór Leibniza

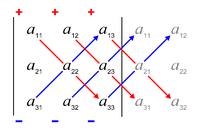
Wzór Leibniza na wyznacznik macierzy 3 × 3 jest następujący:

${\ Displaystyle {\ zacząć {wyrównany} {\ zacząć {vmatrix} a&b&c\\d&e&f\\g&h&i\end {vmatrix}}&=a(ei-fh)-b(di-fg)+c(dh-eg) \\&=aei+bfg+cdh-ceg-bdi-afh.\end{wyrównany}}}$

Reguła sarrusa jest pamięciowy dla tego wzoru: suma produktów z trzech przekątnej północny-zachód do linii południowo-wschodniej części elementów macierzy, minus suma produktów z trzech przekątnej południowym zachodzie do północno-wschodniej linii pierwiastków , gdy obok niej napisane są kopie dwóch pierwszych kolumn matrycy, jak na ilustracji:

Ten schemat obliczania wyznacznika macierzy 3 × 3 nie przenosi się na wyższe wymiary.

n × n macierze

Formuła Leibniza na wyznacznik macierzy -jest bardziej złożonym , ale powiązanym wyrażeniem. Jest to wyrażenie obejmujące pojęcie permutacji i ich sygnaturę . Permutacja zbioru to funkcja, która zmienia kolejność tego zbioru liczb całkowitych. Wartość na -tej pozycji po zmianie kolejności jest oznaczona przez . Zbiór wszystkich takich permutacji, tzw. grupa symetryczna , jest oznaczony . Sygnaturę określa się, gdy zmiana kolejności podana przez σ może być osiągnięta przez sukcesywną zamianę dwóch wpisów parzystą liczbę razy, i zawsze, gdy można to osiągnąć przez nieparzystą liczbę takich wymian. Biorąc pod uwagę macierz i permutację , iloczyn ${\displaystyle n\razy n}$${\ Displaystyle A}$${\ Displaystyle \ {1,2, \ kropki, n \}}$ ${\displaystyle \sigma}$${\displaystyle i}$${\displaystyle \sigma}$${\ Displaystyle \ sigma _ {i}}$${\displaystyle S_{n}}$${\displaystyle \sigma}$${\displaystyle +1}$${\ Displaystyle -1}$${\ Displaystyle A}$${\displaystyle \sigma}$

${\ Displaystyle a_ {1, \ sigma _ {1}} \ cdot a_ {2, \ sigma _ {2}} \ cdot \ kropki \ cdot a_ {n, \ sigma _ {n}}}$

jest również napisane krócej za pomocą notacji Pi, jako

${\ Displaystyle \ prod _ {i = 1} ^ {n} a_ {i, \ sigma _ {i}}}$.

Używając tych pojęć, definicja wyznacznika za pomocą wzoru Leibniza to:

${\ Displaystyle \ det (A) = \ suma _ {\ sigma \ w S_ {n}} \ lewo (\ nazwa operatora {sgn} (\ sigma) \ prod _ {i = 1} ^ {n} a_ {i, \sigma _{i}}\prawda),}$

suma obejmująca wszystkie permutacje, gdzie każda suma jest iloczynem wpisów macierzy pomnożonych przez znak w zależności od permutacji.

Poniższa tabela rozwija te terminy w przypadku . W pierwszej kolumnie permutacja jest wymieniona zgodnie z jej wartościami. Na przykład w drugim rzędzie permutacja spełnia . Można go uzyskać ze zlecenia standardowego (1, 2, 3) przez pojedynczą giełdę (zamiana drugiego i trzeciego wpisu), tak aby jego podpis był . ${\displaystyle n=3}$${\displaystyle \sigma}$${\ Displaystyle \ sigma _ {1} = 1 \ sigma _ {2} = 3 \ sigma _ {3} = 2}$${\displaystyle \operatorname {sgn}(\sigma)=-1}$

Permutacje i ich wkład w wyznacznik ${\ Displaystyle \ {1,2,3 \}}$

Permutacja ${\displaystyle \sigma}$	${\displaystyle \operatorname {sgn} (\sigma)}$	${\ Displaystyle \ operatorname {sgn} (\ sigma) \ prod _ {i = 1} ^ {n} a_ {i \ sigma _ {i}}}$
1, 2, 3	${\displaystyle +1}$	${\ Displaystyle + a_ {1,1} a_ {2,2} a_ {3,3}}$
1, 3, 2	${\ Displaystyle -1}$	${\ Displaystyle -a_ {1,1} a_ {2,3} a_ {3,2}}$
3, 1, 2	${\displaystyle +1}$	${\ Displaystyle + a_ {1,3} a_ {2,1} a_ {3,2}}$
3, 2, 1	${\ Displaystyle -1}$	${\ Displaystyle -a_ {1,3} a_ {2,2} a_ {3,1}}$
2, 3, 1	${\displaystyle +1}$	${\ Displaystyle + a_ {1,2} a_ {2,3} a_ {3,1}}$
2, 1, 3	${\ Displaystyle -1}$	${\ Displaystyle -a_ {1,2} a_ {2,1} a_ {3,3}}$

Suma sześciu warunków w trzeciej kolumnie brzmi

${\ Displaystyle \ suma _ {\ sigma \ w S_ {3}} \ nazwa operatora {sgn} (\ sigma) \ prod _ {i = 1} ^ {n} a_ {i, \ sigma _ {i}} = a_ {1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}+a_{1,3}a_{2,1}a_ {3,2}-a_{1,3}a_{2,2}a_{3,1}+a_{1,2}a_{2,3}a_{3,1}-a_{1,2} a_{2,1}a_{3,3}.}$

Daje to z powrotem wzór na -macierze powyżej. Dla ogólnej macierzy wzór Leibniza obejmuje ( n silni ) sumy, z których każda jest iloczynem n wpisów macierzy. ${\displaystyle 3\razy 3}$${\displaystyle n\razy n}$${\displaystyle n!}$

Wzór Leibniza można również wyrazić za pomocą sumowania, w którym występują nie tylko permutacje, ale wszystkie sekwencje indeksów w zakresie . W tym celu zamiast znaku permutacji używa się symbolu Levi-Civita${\ Displaystyle n}$${\displaystyle 1,\kropki,n}$ ${\ Displaystyle \ varepsilon _ {i_ {1}, \ cdots, i_ {n}}}$

${\ Displaystyle \ det (A) = \ suma _ {i_ {1}, i_ {2}, \ ldots, i_ {n} = 1} ^ {n} \ varepsilon _ {i_ {1} \ cdots i_ {n }}a_{1,i_{1}}\cdots a_{n,i_{n}},}$

Daje to powyższy wzór, ponieważ symbol Levi-Civita wynosi zero, jeśli indeksy nie tworzą permutacji. ${\displaystyle ja_{1},\kropki,i_{n}}$

Właściwości wyznacznika

Charakterystyka wyznacznika

Wyznacznik można scharakteryzować za pomocą następujących trzech kluczowych właściwości. Aby to stwierdzić, wygodnie jest uznać macierz A jako złożoną z jej kolumn, tak oznaczoną jako ${\displaystyle n\razy n}$${\ Displaystyle n}$

${\ Displaystyle A = {\ duży (} a_ {1}, \ kropki, a_ {n} {\ duży )},}$

gdzie wektor kolumnowy (dla każdego i ) składa się z wpisów macierzy w i- tej kolumnie. ${\displaystyle a_{i}}$

2. ${\ Displaystyle \ det \ lewo (ja \ prawo) = 1}$, gdzie jest macierzą tożsamości .${\ Displaystyle I}$
4. Wyznacznik jest wieloliniowy : jeśli j- ta kolumna macierzy jest zapisana jako liniowa kombinacja dwóch wektorów kolumnowych v i w oraz liczby r , to wyznacznik A można wyrazić jako podobną kombinację liniową: ${\ Displaystyle A}$ ${\ Displaystyle a_ {j} = r \ cdot v + w}$

   ${\ Displaystyle {\ zacząć {wyrównany} | A | & = {\ duży |} a_ {1}, \ kropki, a_ {j-1}, r \ cdot v + w, a_ {j + 1}, \ kropki ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n} |\end{wyrównany}}}$

6. Wyznacznik jest naprzemienny : ilekroć dwie kolumny macierzy są identyczne, jej wyznacznikiem jest 0:

   ${\ Displaystyle | a_ {1}, \ kropki, v, \ kropki, v, \ kropki, a_ {n} | = 0.}$

Jeśli wyznacznik jest zdefiniowany za pomocą wzoru Leibniza jak powyżej, te trzy właściwości można udowodnić przez bezpośrednią kontrolę tego wzoru. Niektórzy autorzy również podchodzą do wyznacznika bezpośrednio posługując się tymi trzema właściwościami: można wykazać, że istnieje dokładnie jedna funkcja, która przypisuje dowolnej -macierz A liczbę spełniającą te trzy właściwości. Pokazuje to również, że bardziej abstrakcyjne podejście do wyznacznika daje taką samą definicję, jak przy użyciu wzoru Leibniza. ${\displaystyle n\razy n}$

Aby to zobaczyć, wystarczy rozszerzyć wyznacznik o wieloliniowość w kolumnach do (ogromnej) liniowej kombinacji wyznaczników macierzy, w której każda kolumna jest standardowym wektorem bazowym. Te wyznaczniki to albo 0 (według właściwości 9) albo ±1 (według właściwości 1 i 12 poniżej), więc kombinacja liniowa daje powyższe wyrażenie w postaci symbolu Levi-Civita. Choć z pozoru mniej technicznego, charakterystyka ta nie może całkowicie zastąpić formuły Leibniza w definiowaniu wyznacznika, ponieważ bez niej istnienie odpowiedniej funkcji nie jest jasne.

Natychmiastowe konsekwencje

Zasady te mają kilka dalszych konsekwencji:

• Wyznacznikiem jest funkcja jednorodna , tj.

${\ Displaystyle \ det (cA) = c ^ {n} \ det (A)}$(dla macierzy ).${\displaystyle n\razy n}$${\ Displaystyle A}$

• Zamiana dowolnej pary kolumn macierzy mnoży jej wyznacznik przez -1. Wynika to z wyznacznika wieloliniowego i przemiennego (właściwości 2 i 3 powyżej):

${\ Displaystyle | a_ {1}, \ kropki, a_ {j}, \ kropki a_ {i}, \ kropki, a_ {n} | = - | a_ {1}, \ kropki, a_ {i}, \ kropki ,a_{j},\kropki ,a_{n}|.}$

Ta formuła może być stosowana iteracyjnie w przypadku zamiany kilku kolumn. Na przykład

${\ Displaystyle | a_ {3}, a_ {1}, a_ {2}, a_ {4} \ kropki, a_ {n} | = - | a_ {1}, a_ {3}, a_ {2}, a_ {4},\kropki,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\kropki,a_{n}|.}$

Jeszcze bardziej ogólnie, każda permutacja kolumn mnoży wyznacznik przez znak permutacji.

• Jeśli jakaś kolumna może być wyrażona jako liniowa kombinacja innych kolumn (tj. kolumny macierzy tworzą zbiór liniowo zależny ), wyznacznikiem jest 0. W szczególnym przypadku obejmuje to: jeśli jakaś kolumna jest taka, że ​​wszystkie jej wpisy są zerowe, to wyznacznikiem tej macierzy jest 0.
• Dodanie skalarnej wielokrotności jednej kolumny do innej kolumny nie zmienia wartości wyznacznika. Jest to konsekwencja wieloliniowości i bycia alternatywnym: przez wieloliniowość wyznacznik zmienia się o wielokrotność wyznacznika macierzy o dwóch równych kolumnach, której wyznacznikiem jest 0, ponieważ wyznacznik jest naprzemienny.
• Jeżeli jest macierzą trójkątną , czyli , kiedykolwiek lub alternatywnie, kiedykolwiek , to jej wyznacznik jest równy iloczynowi przekątnych:${\ Displaystyle A}$${\displaystyle a_{ij}=0}$${\displaystyle i>j}$${\displaystyle i<j}$

${\ Displaystyle \ det (A) = a_ {11} a_ {22} \ cdots a_ {nn} = \ prod _ {i = 1} ^ {n} a_ {ii}.}$

Rzeczywiście, taką macierz można zredukować, odpowiednio dodając wielokrotności kolumn z mniejszą liczbą wpisów niezerowych do tych z większą liczbą wpisów, do macierzy diagonalnej (bez zmiany wyznacznika). Dla takiej macierzy, użycie liniowości w każdej kolumnie sprowadza się do macierzy identyczności, w którym to przypadku podany wzór jest zgodny z pierwszą cechą charakterystyczną wyznaczników. Alternatywnie ten wzór można również wywnioskować ze wzoru Leibniza, ponieważ jedyną permutacją, która daje niezerowy wkład, jest permutacja tożsamości.${\displaystyle \sigma}$

Przykład

Wymienione powyżej właściwości charakteryzujące i ich konsekwencje są zarówno istotne teoretycznie, jak i mogą być również wykorzystywane do obliczania wyznaczników macierzy betonowych. W rzeczywistości eliminację Gaussa można zastosować do sprowadzenia dowolnej macierzy do postaci górnego trójkąta, a kroki tego algorytmu wpływają na wyznacznik w kontrolowany sposób. Poniższy konkretny przykład ilustruje obliczanie wyznacznika macierzy przy użyciu tej metody: ${\ Displaystyle A}$

${\ Displaystyle A = {\ zacząć {bmatrix} -2 i -1 i 2 \ \ 2 i 1 i 4 \ \ -3 i 3 i 1 \ koniec {bmatrix}}.}$

Tekst podpisu

Matryca	${\ Displaystyle B = {\ zacząć {bmatrix} 3 i 1 i 2 \ \ 3 i 1 i 4 \ \ 0 i 3 i 1 \ koniec {bmatrix}}}$	${\ Displaystyle C = {\ zacząć {bmatrix} 3 i 5 i 2 \ \ 3 i 13 i 4 \ \ 0 i 0 i 1 \ koniec {bmatrix}}}$	${\ Displaystyle D = {\ zacząć {bmatrix} 5 i 3 i 2 \ \ 13 i 3 i 4 \ \ 0 i 0 i 1 \ koniec {bmatrix}}}$	${\ Displaystyle E = {\ zacząć {bmatrix} 18 i 3 i 2 \ \ 0 i 3 i 4 \ \ 0 i 0 i 1 \ koniec {bmatrix}}}$
Zdobyty przez	dodaj drugą kolumnę do pierwszej	dodaj 3 razy trzecią kolumnę do drugiej	zamień pierwsze dwie kolumny	dodaj razy drugą kolumnę do pierwszej ${\displaystyle -{\frac {13}{3}}}$
Wyznacznik	${\displaystyle |A|=|B|}$	${\displaystyle |B|=|C|}$	${\displaystyle |D|=-|C|}$	${\displaystyle |E|=|D|}$

Połączenie tych równości daje ${\ Displaystyle | A | = - | E | = -18 \ cdot 3 \ cdot (-1) = 54.}$

Transponować

Wyznacznikiem Transpozycja o równy wyznacznik A : ${\ Displaystyle A}$

${\ Displaystyle \ DET \ lewo (A ^ {\ textsf {T}} \ po prawej) = \ DET (A)}$.

Można to udowodnić, sprawdzając formułę Leibniza. Oznacza to, że we wszystkich właściwościach wymienionych powyżej słowo „kolumna” można w całym tekście zastąpić słowem „wiersz”. Na przykład, patrząc na macierz n × n jako złożoną z n wierszy, wyznacznikiem jest funkcja n- liniowa.

Multiplikatywność i grupy macierzowe

Zatem wyznacznikiem jest odwzorowanie multiplikatywne , tj. dla macierzy kwadratowych i równej wielkości wyznacznik iloczynu macierzy jest równy iloczynowi ich wyznaczników: ${\ Displaystyle A}$${\ Displaystyle B}$

${\ Displaystyle \ det (AB) = \ det (A) \ det (B)}$

Ten kluczowy fakt można udowodnić, obserwując, że dla stałej macierzy , obie strony równania są przemienne i wieloliniowe jako funkcja w zależności od kolumn . Co więcej, oba przyjmują wartość, gdy jest macierzą tożsamości. Wspomniana powyżej unikalna charakterystyka przemiennych map wieloliniowych pokazuje zatem to twierdzenie. ${\ Displaystyle B}$${\ Displaystyle A}$${\displaystyle \det B}$${\ Displaystyle A}$

Macierz jest odwracalna dokładnie, jeśli jej wyznacznik jest niezerowy. Wynika to z multiplikatywności i wzoru na odwrotność macierzy sprzężonej wymienionej poniżej. W tym przypadku wyznacznik macierzy odwrotnej jest podany przez ${\ Displaystyle A}$${\displaystyle \det}$

${\ Displaystyle \ DET \ lewo (A ^ {-1} \ po prawej) = {\ Frac {1} {\ Det (A)}} = [\ DET (A)] ^ {-1}}$.

W szczególności iloczyny i odwrotności macierzy z niezerową determinantą (odpowiednio determinantą) nadal mają tę właściwość. Tak więc zbiór takich macierzy (o ustalonym rozmiarze ) tworzy grupę znaną jako ogólna grupa liniowa (odpowiednio podgrupa zwana specjalną grupą liniową . Bardziej ogólnie, słowo „specjalna” oznacza podgrupę innej grupy macierzy macierzy o wyznacznikiem 1. Przykładami są specjalna grupa ortogonalna (która, jeśli n wynosi 2 lub 3, to wszystkie macierze rotacji ) oraz specjalna grupa unitarna . ${\ Displaystyle n}$ ${\ Displaystyle \ Operatorname {GL} _ {n}}$ ${\ Displaystyle \ operatorname {SL} _ {n} \ podzbiór \ operatorname {GL} _ {n}}$

Wzór Cauchy'ego-Bineta jest uogólnieniem tego wzoru iloczynowego dla macierzy prostokątnych . Wzór ten można również przekształcić w wzór multiplikatywny dla macierzy złożonych, których wpisy są wyznacznikami wszystkich podmacierzy kwadratowych danej macierzy.

Ekspansja Laplace'a

Rozwinięcie Laplace'a wyraża wyznacznik macierzy w postaci wyznaczników mniejszych macierzy, zwanych jej podrzędnymi . Drugorzędna jest zdefiniowana jako wyznacznik macierzy, która wynika z usunięcia -tego wiersza i -tej kolumny. Wyrażenie jest znane jako kofaktor . Dla każdego ma się równość ${\ Displaystyle A}$${\ Displaystyle M_ {i, j}}$${\displaystyle (n-1)\razy (n-1)}$${\ Displaystyle A}$${\displaystyle i}$${\displaystyle j}$${\ Displaystyle (-1) ^ {i + j} M_ {i, j}}$${\displaystyle i}$

${\ Displaystyle \ det (A) = \ suma _ {j = 1} ^ {n} (-1) ^ {i + j} a_ {ij} M_ {ij}}$

co nazywa się ekspansją Laplace'a wzdłuż i- tego rzędu . Na przykład rozwinięcie Laplace'a wzdłuż pierwszego wiersza ( ) daje następującą formułę: ${\displaystyle i=1}$

${\displaystyle {\zacząć{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\zacząć{vmatrix}e&f\\h&i\end{vmatrix}}-b{\zacząć{vmatrix}d&f\ \g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}}$

Rozwinięcie wyznaczników tych macierzy daje z powrotem wspomnianą wyżej formułę Leibniza. Podobnie rozwinięcie Laplace'a wzdłuż -tej kolumny to równość ${\displaystyle 2\razy 2}$${\displaystyle j}$

${\ Displaystyle \ det (A) = \ suma _ {i = 1} ^ {n} (-1) ^ {i + j} a_ {ij} M_ {ij}.}$

Rozszerzenie Laplace'a może być używane iteracyjnie do obliczania wyznaczników, ale to podejście jest nieefektywne w przypadku dużych macierzy. Jest jednak przydatny do obliczania wyznaczników wysoce symetrycznej macierzy, takiej jak macierz Vandermonde

${\ Displaystyle \ lewo | {\ zacząć {tablica} {ccccc} 1 i 1 i 1 i \ cdots i 1 \ \ x_ {1} i x_ {2} i x_ {3} i \ cdots i x_ {n} \ \ x_ {1} ^ {2} &x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^ {n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{array}}\right|=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).}$

Wyznacznik ten został zastosowany np. w dowodzie twierdzenia Bakera w teorii liczb przestępnych .

Macierz sprzężenia

Matrycy adjugate jest transpozycję macierzy kofaktorów, to znaczy ${\ Displaystyle \ Operatorname {przym.} (A)}$

${\ Displaystyle (\ nazwa operatora {przym.} (A)) _ {ij} = (-1) ^ {i + j} M_ {ji}.}$

Na każdą macierz przypada

${\ Displaystyle (\det A) I = A \ nazwa operatora {przym.} A = (\ nazwa operatora {przym.} A) \ A.}$

Zatem macierz sprzężona może być użyta do wyrażenia odwrotności macierzy nieosobliwej :

${\ Displaystyle A ^ {-1} = {\ Frac {1} {\ Det A}} \ Operatorname {przym.} A.}$

Macierze blokowe

Powyższy wzór na wyznacznik a- macierzy nadal utrzymuje, przy odpowiednich dalszych założeniach, macierz blokową , tj. macierz złożoną z czterech podmacierzy o wymiarach odpowiednio , , i . Najłatwiejszą taką formułą, którą można udowodnić za pomocą formuły Leibniza lub faktoryzacji z udziałem dopełnienia Schura , jest ${\displaystyle 2\razy 2}$${\displaystyle A,B,C,D}$${\displaystyle n\razy n}$${\displaystyle n\razy m}$${\displaystyle m\razy n}$${\displaystyle m\razy m}$

${\ Displaystyle \ det {\ zacząć {pmatrix} A i 0 \ \ C i D \ koniec {pmatrix}} = \ det (A) \ det (D) = \ det {\ zacząć {pmatrix} A & B \ \ 0 i D \ koniec {pmatrix} }.}$

Jeśli jest odwracalny (i podobnie, jeśli jest odwracalny), trzeba: ${\ Displaystyle A}$${\ Displaystyle D}$

${\ Displaystyle \ det {\ zacząć {pmatrix} A & B \ \ C & D \ koniec {pmatrix}} = \ det (A) \ det \ po lewej (D-CA ^ {-1} B \ po prawej).}$

Jeśli jest -macierzą, upraszcza się to do . ${\ Displaystyle D}$${\displaystyle 1\razy 1}$${\ Displaystyle \ det (A) (D-CA ^ {-1} B)}$

Jeśli bloki są macierzami kwadratowymi o tym samym rozmiarze, obowiązują dalsze formuły. Na przykład, jeśli i dojeżdżać (tj. ), to trzyma się ${\displaystyle C}$${\ Displaystyle D}$ ${\ Displaystyle CD = DC}$

${\displaystyle \det {\rozpocząć{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).}$

Wzór ten został uogólniony na macierze złożone z więcej niż bloków, ponownie w odpowiednich warunkach przemienności między poszczególnymi blokami. ${\displaystyle 2\razy 2}$

Dla i obowiązuje następujący wzór (nawet jeśli i i B nie dojeżdżają) ${\ Displaystyle A = D}$${\ Displaystyle B = C}$${\ Displaystyle A}$${\ Displaystyle B}$

${\displaystyle \det {\rozpocząć{pmatrix}A&B\\B&A\end{pmatrix}}=\det(AB)\det(A+B).}$

Twierdzenie o wyznaczniku Sylwestra

Determinant twierdzenie Sylvester stwierdza się, że na A , w m x n matrycy i B , z n x m matrycy (tak i B mają wymiary umożliwiające ich mnoży się w dowolnej kolejności, tworząc macierz kwadratową)

${\ Displaystyle \ DET \ lewo (I_ {\ mathit {m}} + AB \ prawej) = \ Det \ lewo (I_ {\ mathit {n}} + BA \ po prawej)}$

gdzie I _m i I _n są odpowiednio macierzami tożsamości m × m i n × n .

Z tego ogólnego wyniku wynika kilka konsekwencji.

Suma

Wyznacznik sumy dwóch macierzy kwadratowych o tym samym rozmiarze nie jest na ogół wyrażalny jako wyznaczniki A i B . Jednakże, w przypadku pozytywnych półokreśloną matryc , i jednakowej wielkości, na z następstwie${\displaystyle A+B}$ ${\ Displaystyle A}$${\ Displaystyle B}$${\displaystyle C}$${\ Displaystyle \ det (A + B + C) + \ det (C) \ geq \ det (A + C) + \ det (B + C)}$${\displaystyle A,B,C\geq 0}$${\ Displaystyle \ det (A + B) \ geq \ det (A) + \ det (B).}$

Własności wyznacznika w stosunku do innych pojęć

Wartości własne i wielomian charakterystyczny

Wyznacznik jest ściśle powiązany z dwoma innymi centralnymi pojęciami w algebrze liniowej, wartościami własnymi i charakterystycznym wielomianem macierzy. Niech będzie macierzą ze złożonymi wpisami z wartościami własnymi . (Tutaj rozumie się, że wartość własna z krotnością algebraiczną μ występuje na tej liście razy μ .) Wtedy wyznacznikiem A jest iloczyn wszystkich wartości własnych, ${\ Displaystyle A}$${\displaystyle n\razy n}$ ${\ Displaystyle \ lambda _ {1} \ lambda _ {2} \ ldots \ lambda _ {n}}$

${\ Displaystyle \ det (A) = \ prod _ {i = 1} ^ {n} \ lambda _ {i} = \ lambda _ {1} \ lambda _ {2} \ cdots \ lambda _ {n}.}$

Iloczyn wszystkich niezerowych wartości własnych jest określany jako pseudodeterminant .

Wielomian charakterystyczny jest zdefiniowany jako

${\ Displaystyle \ chi _ {A} (t) = \ operatorname {det} (t \ cdot IA).}$

Tutaj jest nieokreślony wielomianu i jest macierzą jednostkową o takim samym rozmiarze jak . Za pomocą tego wielomianu wyznaczniki można wykorzystać do znalezienia wartości własnych macierzy : są to dokładnie pierwiastki tego wielomianu, tj. te liczby zespolone , które ${\displaystyle t}$${\ Displaystyle I}$${\ Displaystyle A}$${\ Displaystyle A}$${\ Displaystyle \ lambda}$

${\ Displaystyle \ chi _ {A} (\ lambda) = 0.}$

Hermitowskie matryca jest pozytywny określony , jeżeli wszystkie jej wartości własne są dodatnie. Kryterium Sylwestra zakłada, że ​​jest to równoważne wyznacznikom podmacierzy

${\ Displaystyle A_ {k}: = {\ zacząć {bmatrix} a_ {1,1} i a_ {1,2} i \ kropki i a_ {1, k} \ \ a_ {2,1} i a_ {2,2} &\dots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\kropki &a_{k,k}\end{bmatrix} }.}$

bycie pozytywnym, dla wszystkich pomiędzy i . ${\displaystyle k}$${\ Displaystyle 1}$${\ Displaystyle n}$

Namierzać

Ślad tr ( ) jest z definicji suma przekątnych wpisów A i również jest równa sumie wartości własnych. Tak więc dla złożonych macierzy A ,

${\displaystyle \det(\exp(A))=\exp(\operator {tr}(A))}$

lub dla rzeczywistych macierzy A ,

${\displaystyle \operatorname {tr}(A)=\log(\det(\exp(A))).}$

Tutaj exp ( ) oznacza macierz wykładniczy od A , ponieważ każda wartość własna λ od A odpowiada wartości własnej ważności ( λ ) exp ( ). W szczególności, mając dowolny logarytm z A , czyli dowolną macierz L spełniającą

${\ Displaystyle \ exp (L) = A}$

wyznacznik A jest podany przez

${\displaystyle \det(A)=\exp(\operator {tr}(L)).}$

Na przykład, odpowiednio dla n = 2 , n = 3 i n = 4 ,

${\ Displaystyle {\ zacząć {wyrównany} \ det (A) i = {\ Frac {1} {2}} \ lewo (\ lewo (\ nazwa operatora {tr} (A) \ po prawej) ^ {2} - \ nazwa operatora {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A )\right)^{3}-3\nazwa operatora {tr} (A)~\nazwa operatora {tr} \left(A^{2}\right)+2\nazwa operatora {tr} \left(A^{3} \right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\ operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2 }\right)\right)^{2}+8\operator {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^ {4}\right)\right).\end{aligned}}}$

por. Twierdzenie Cayleya-Hamiltona . Takie wyrażenia można wyprowadzić z argumentów kombinatorycznych, tożsamości Newtona lub algorytmu Faddeeva-LeVerriera . Oznacza to, że dla rodzaju n , det A = (−1) ⁿ c ₀ człon stały ze znakiem charakterystycznego wielomianu , wyznaczony rekursywnie z

${\ Displaystyle c_ {n} = 1; ~ ~ ~ c_ {nm} = - {\ Frac {1} {m}} \ suma _ {k = 1} ^ {m} c_ {n-m + k} \ operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.}$

W ogólnym przypadku można to również uzyskać z

${\ Displaystyle \ det (A) = \ suma _ {\ zacząć {tablica} {c} k_ {1}, k_ {2}, \ ldots, k_ {n} \ geq 0 \ \ k_ {1} +2 k_ { 2}+\cdots +nk_{n}=n\end{tablica}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l ^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},}$

gdzie suma jest przejmowana przez zbiór wszystkich liczb całkowitych k _l ≥ 0 spełniających równanie

${\ Displaystyle \ suma _ {l = 1} ^ {n} lk_ {l} = n.}$

Wzór może być wyrażony w postaci pełnego wykładniczego wielomianu Bella o n argumentach s _l = −( l – 1)! tR ( ^l ), a

${\ Displaystyle \ det (A) = {\ Frac {(-1) ^ {n}} {n!}} B_ {n} (s_ {1}, s_ {2}, \ ldots, s_ {n}) .}$

Wzór ten może być również użyty do znalezienia wyznacznika macierzy A ^I _J o wielowymiarowych indeksach I = (i ₁ , i ₂ , ..., i _r ) oraz J = (j ₁ , j ₂ , ..., j _r ) . Iloczyn i ślad takich matryc określa się w sposób naturalny jako:

${\ Displaystyle (AB) _ {J} ^ {I} = \ suma _ {K} A_ {K} ^ {I} B_ {J} ^ {K} \ Operatorname {tr} (A) = \ suma _ {I}A_{I}^{I}.}$

Ważny arbitralny wymiar n tożsamości można uzyskać z rozwinięcia logarytmu w szereg Mercatora, gdy rozwinięcie jest zbieżne. Jeśli każda wartość własna A jest mniejsza niż 1 w wartości bezwzględnej,

${\ Displaystyle \ det (I + A) = \ suma _ {k = 0} ^ {\ infty} {\ Frac {1} {k!}} \ lewo (- \ suma _ {j = 1} ^ {\ infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

gdzie ja jest macierzą tożsamości. Bardziej ogólnie, jeśli

${\ Displaystyle \ suma _ {k = 0} ^ {\ infty} {\ Frac {1} {k!}} \ lewo (- \ suma _ {j = 1} ^ {\ infty} {\ Frac {(- 1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

jest rozwinięty jako formalny szereg potęgowy w s wtedy wszystkie współczynniki s ^m dla m > n wynoszą zero, a pozostały wielomian to det( I + sA ) .

Granice górne i dolne

Dla dodatniej określonej macierzy A , operator śladu daje następujące ścisłe dolne i górne granice wyznacznika logarytmicznego

${\ Displaystyle \ operatorname {tr} \ lewo (IA ^ {-1} \ prawo) \ leq \ log \ det (A) \ leq \ operatorname {tr} (AI)}$

z równością wtedy i tylko wtedy, gdy A = I . Zależność tę można wyprowadzić ze wzoru na rozbieżność KL między dwoma wielowymiarowymi rozkładami normalnymi .

Także,

${\ Displaystyle {\ Frac {n} {\ Operatorname {tr} \ lewo (A ^ {-1} \ prawej)}} \ leq \ det (A) ^ {\ Frac {1} {n}} \ leq { \frac {1}{n}}\nazwa operatora {tr} (A)\leq {\sqrt {{\frac {1}{n}}\nazwa operatora {tr} \left(A^{2}\right)} }.}$

Nierówności te można udowodnić, sprowadzając macierz A do postaci diagonalnej. Jako takie reprezentują dobrze znany fakt, że średnia harmoniczna jest mniejsza niż średnia geometryczna , która jest mniejsza niż średnia arytmetyczna , która z kolei jest mniejsza niż średnia kwadratowa .

Pochodna

Ze wzoru Leibniza wynika, że ​​wyznacznikiem rzeczywistych (lub analogicznie dla złożonych) macierzy kwadratowych jest funkcja wielomianowa od do . W szczególności jest wszędzie różnicowa . Jego pochodną można wyrazić za pomocą wzoru Jacobiego : ${\ Displaystyle \ mathbf {R} ^ {n \ razy n}}$${\ Displaystyle \ mathbf {R} }$

${\ Displaystyle {\ Frac {d \ det (A)} {d \ alfa}} = \ operatorname {tr} \ lewo (\ operatorname {przym} (A) {\ Frac {dA} {d \ alfa}} \ Prawidłowy).}$

gdzie oznacza adjugate się . W szczególności, jeśli jest odwracalny, mamy ${\ Displaystyle \ Operatorname {przym.} (A)}$${\ Displaystyle A}$${\ Displaystyle A}$

${\ Displaystyle {\ Frac {d \ det (A)} {d \ alfa}} = \ det (A) \ operatorname {tr} \ lewo (A ^ {-1} {\ Frac {dA} {d \ alfa }}\Prawidłowy).}$

Wyrażone w kategoriach wpisów , są to ${\ Displaystyle A}$

${\ Displaystyle {\ Frac {\ częściowy \ det (A)} {\ częściowy A_ {ij}}} = \ operatorname {przym.} (A) _ {ji} = \ det (A) \ lewo (A ^ {- 1}\right)_{ji}.}$

Jeszcze innym równoważnym sformułowaniem jest

${\ Displaystyle \ det (A + \ epsilon X) - \ det (A) = \ operatorname {tr} (\ operatorname {przym.} (A) X) \ epsilon + O \ lewo (\ epsilon ^ {2} \ po prawej) =\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)}$,

przy użyciu notacji duże O . Szczególny przypadek, w którym , macierz jednostkowa, daje ${\displaystyle A=I}$

${\ Displaystyle \ det (I + \ epsilon X) = 1 + \ nazwa operatora {tr} (X) \ epsilon + O \ lewo (\ epsilon ^ {2} \ po prawej).}$

Ta tożsamość jest używana w opisie algebr Liego związanych z pewnymi macierzowymi grupami Liego . Na przykład specjalna grupa liniowa jest zdefiniowana równaniem . Powyższy wzór pokazuje, że jego algebra Liego jest specjalną algebrą liniową Liego składającą się z tych macierzy, które mają ślad zero. ${\ Displaystyle \ operatorname {SL} _ {n}}$${\ Displaystyle \ Det A = 1}$ ${\ Displaystyle {\ mathfrak {sl}} _ {n}}$

Pisząc macierz - gdzie są wektory kolumnowe o długości 3, to gradient nad jednym z trzech wektorów można zapisać jako iloczyn krzyżowy dwóch pozostałych: ${\displaystyle 3\razy 3}$${\ Displaystyle A = {\ zacząć {bmatrix} a & b & c \ koniec {bmatrix}}}$${\displaystyle a,b,c}$

${\ Displaystyle {\ zacząć {wyrównany} \ nabla _ {\ mathbf {a}} \ det (A) & = \ mathbf {b} \ razy \ mathbf {c} \ \ \ nabla _ {\ mathbf {b}} \det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\koniec{wyrównany}}}$

Historia

Historycznie wyznaczniki były używane na długo przed macierzami: wyznacznik był pierwotnie definiowany jako właściwość układu równań liniowych . Wyznacznik „określa”, czy system ma jednoznaczne rozwiązanie (które występuje właśnie wtedy, gdy wyznacznik jest niezerowy). W tym sensie wyznaczniki zostały po raz pierwszy użyte w chińskim podręczniku matematyki The Nine Chapters on the Mathematical Art (九章算術, chińscy uczeni, około III wieku p.n.e.). W Europie rozwiązania układów liniowych dwóch równań zostały wyrażone przez Cardano w 1545 r. przez podmiot podobny do wyznacznika.

Właściwe wyznaczniki wywodzą się z prac Seki Takakazu w 1683 w Japonii i równolegle Leibniza w 1693. Cramer (1750) podał bez dowodu rządy Cramera. Zarówno Cramer, jak i Bezout (1779) zostały sprowadzone do wyznaczników przez kwestię krzywych płaskich przechodzących przez dany zbiór punktów.

Vandermonde (1771) jako pierwszy rozpoznał determinanty jako funkcje niezależne. Laplace (1772) podał ogólną metodę rozszerzania wyznacznika w zakresie jego uzupełniających się nieletnich : Vandermonde podał już przypadek szczególny. Zaraz potem Lagrange (1773) potraktował wyznaczniki drugiego i trzeciego rzędu i zastosował je do zagadnień teorii eliminacji ; udowodnił wiele szczególnych przypadków tożsamości ogólnych.

Gauss (1801) dokonał kolejnego postępu. Podobnie jak Lagrange, często wykorzystywał wyznaczniki w teorii liczb . On wprowadził słowo „wyznacznik” (Laplace użył „wypadkowa”), choć nie w obecnym znaczeń, lecz raczej jako stosowane do wyróżnika z Quantic . Gauss doszedł również do pojęcia wyznaczników odwrotnych (odwrotnych) i bardzo zbliżył się do twierdzenia o mnożeniu.

Kolejnym ważnym kontrybutorem jest Binet (1811, 1812), który formalnie sformułował twierdzenie odnoszące się do iloczynu dwóch macierzy m kolumn i n wierszy, które dla szczególnego przypadku m = n sprowadza się do twierdzenia o mnożeniu. Tego samego dnia (30 listopada 1812), w którym Binet przedstawił swoją pracę w Akademii, Cauchy przedstawił również jeden na ten temat. (Patrz wzór Cauchy-Bineta .) W tym przypadku użył słowa „wyznacznik” w jego obecnym znaczeniu, podsumował i uprościł to, co było wówczas znane na ten temat, poprawił notację i dał twierdzenie o mnożeniu z dowodem bardziej zadowalającym niż Bineta. Wraz z nim zaczyna się teoria w jej ogólności.

( Jacobi 1841 ) użył wyznacznika funkcjonalnego , który Sylvester nazwał później jakobianem . W swoich pamiętnikach w Crelle's Journal z 1841 r. zajmuje się tym tematem, a także klasą funkcji alternatywnych, którą Sylvester nazwał alternantami . Mniej więcej w czasie ostatnich wspomnień Jacobiego Sylvester (1839) i Cayley rozpoczęli swoją pracę. Cayley 1841 wprowadził nowoczesną notację wyznacznika za pomocą pionowych kresek.

Naturalnym rezultatem dopełnienia teorii ogólnej jest badanie szczególnych form determinant. Wyznaczniki osiowosymetryczne badali Lebesgue , Hesse i Sylvester; persymetryczne wyznaczniki Sylwestra i Hankela ; circulants według katalońsku , Spottiswoode'a , Glaisher i Scott; determinanty skośne i Pfaffian , w związku z teorią transformacji ortogonalnej , Cayley; kontynuanty Sylwestra; Wrońscy (tak zwani przez Muira ) przez Christoffela i Frobeniusa ; złożone determinanty Sylwestra, Reissa i Picqueta; Jakobian i Hessians Sylwestra; oraz symetryczne wyznaczniki gauche autorstwa Trudi . Z podręczników na ten temat pierwszy był Spottiswoode. W Ameryce Hanus (1886), Weld (1893) i Muir/Metzler (1933) publikowali traktaty.

Aplikacje

Zasada Cramera

Wyznaczniki mogą służyć do opisu rozwiązań liniowego układu równań , zapisanego w postaci macierzowej jako . To równanie ma unikalne rozwiązanie wtedy i tylko wtedy, gdy jest niezerowe. W tym przypadku rozwiązanie podaje reguła Cramera : ${\ Displaystyle Axe = b}$${\displaystyle x}$${\displaystyle \det(A)}$

${\ Displaystyle x_ {i} = {\ Frac {\ Det (A_ {i})} {\ Det (A)}} \ qquad i = 1,2,3 \ ldots, n}$

gdzie jest macierzą utworzoną przez zastąpienie -tej kolumny wektorem kolumnowym . Wynika to bezpośrednio z rozszerzenia kolumny wyznacznika, tj. ${\ Displaystyle A_ {i}}$${\displaystyle i}$${\ Displaystyle A}$${\displaystyle b}$

${\ Displaystyle \ det (A_ {i}) = \ Det {\ zacząć {bmatrix} a_ {1} i \ ldots & B & \ ldots & a_ {n} \ koniec {bmatrix}} = \ suma _ {j = 1} ^ {n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix} }=x_{i}\det(A)}$

gdzie wektory są kolumnami A . Zasada jest również implikowana przez tożsamość ${\displaystyle a_{j}}$

${\ Displaystyle A \, \ operatorname {przym.} (A) = \ operatorname {przym.} (A) \, A = \ det (A) \ I_ {n}.}$

Reguła Cramera może być zaimplementowana w czasie, co jest porównywalne z bardziej powszechnymi metodami rozwiązywania układów równań liniowych, takimi jak LU , QR , czy dekompozycja na wartości osobliwe . ${\ Displaystyle \ Operatorname {O} (n ^ {3})}$

Liniowa niezależność

Wyznaczników można użyć do scharakteryzowania wektorów zależnych liniowo : wynosi zero wtedy i tylko wtedy, gdy wektory kolumn (lub równoważnie wektory wierszy) macierzy są liniowo zależne. Na przykład, biorąc pod uwagę dwa liniowo niezależne wektory , trzeci wektor leży na płaszczyźnie rozpiętej przez dwa poprzednie wektory dokładnie wtedy, gdy wyznacznik macierzy -składającej się z trzech wektorów wynosi zero. Ta sama idea jest również używana w teorii równań różniczkowych : dane funkcje (ma być różniczkowalne razy ), wroński definiuje się jako ${\displaystyle \det A}$${\ Displaystyle A}$${\ Displaystyle v_ {1}, v_ {2} \ w \ mathbf {R} ^ {3}}$${\displaystyle v_{3}}$ ${\displaystyle 3\razy 3}$${\ Displaystyle f_ {1} (x), \ kropki, f_ {n} (x)}$${\displaystyle n-1}$

${\ Displaystyle W (f_ {1}, \ ldots, f_ {n}) (x) = {\ zacząć {vmatrix} f_ {1} (x) i f_ {2} (x) i \ cdots i f_ {n} ( x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1} ^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}} .}$

Jest niezerowa (dla niektórych ) w określonym przedziale wtedy i tylko wtedy, gdy dane funkcje i wszystkie ich pochodne aż do rzędu są liniowo niezależne. Jeżeli można wykazać, że Wrońskian jest wszędzie na przedziale zero, to w przypadku funkcji analitycznych oznacza to, że dane funkcje są liniowo zależne. Zobacz niezależność wrońską i linearną . Innym takim zastosowaniem wyznacznika jest wynikowa , która daje kryterium , gdy dwa wielomiany mają wspólny pierwiastek . ${\displaystyle x}$${\displaystyle n-1}$

Orientacja podstawy

Wyznacznik mogą być traktowane jako przypisanie do każdego numeru sekwencji z n wektorów w R ⁿ , za pomocą macierzy kwadratowej których kolumny są podane wektory. Na przykład macierz ortogonalna z wpisami w R ⁿ reprezentuje bazę ortonormalną w przestrzeni euklidesowej . Wyznacznik takiej macierzy określa, czy orientacja bazy jest zgodna lub przeciwna do orientacji bazy standardowej . Jeśli wyznacznikiem jest +1, podstawa ma taką samą orientację. Jeśli wynosi -1, podstawa ma przeciwną orientację.

Mówiąc bardziej ogólnie, jeśli wyznacznik A jest dodatni, A reprezentuje transformację liniową zachowującą orientację (jeśli A jest macierzą ortogonalną 2 × 2 lub 3 × 3 , jest to obrót ), natomiast jeśli jest ujemna, A zmienia orientację podstawy.

Wyznacznik objętości i jakobianu

Jak wskazano powyżej, wartość bezwzględna wyznacznika wektorów rzeczywistych jest równa objętości równoległościanu, który obejmuje te wektory. W konsekwencji, jeśli mapa liniowa jest dana przez pomnożenie przez macierz , i jest dowolnym mierzalnym podzbiorem , to objętość dana jest krotnością objętości . Mówiąc ogólnie, jeśli liniowym jest przedstawiony -Matrix , a następnie - trójwymiarowy objętość jest równa: ${\ Displaystyle f: \ mathbf {R} ^ {n} \ do \ mathbf {R} ^ {n}}$${\ Displaystyle A}$${\ Displaystyle S \ podzbiór \ mathbf {R} ^ {n}}$ ${\displaystyle f(S)}$${\displaystyle |\det(A)|}$${\displaystyle S}$${\ Displaystyle f: \ mathbf {R} ^ {n} \ do \ mathbf {R} ^ {m}}$${\displaystyle m\razy n}$${\ Displaystyle A}$${\ Displaystyle n}$${\displaystyle f(S)}$

${\ Displaystyle \ operatorname {objętość} (f (S)) = {\ sqrt {\ det \ lewo (A ^ {\ textsf {T}} A \ po prawej)}} \ operatorname {objętość} (S).}$

Obliczając objętość czworościanu ograniczonego czterema punktami, można je wykorzystać do identyfikacji linii skośnych . Objętość dowolnego czworościanu z uwzględnieniem jego wierzchołków , lub dowolnej innej kombinacji par wierzchołków, które tworzą drzewo opinające nad wierzchołkami. ${\displaystyle a,b,c,d}$${\ Displaystyle {\ Frac {1} {6}} \ cdot | \ det (ab, bc, cd) |}$

Dla ogólnego funkcji różniczkowej , wiele z powyższych przenosi rozważając jakobian matrycy o f . Do

${\ Displaystyle f: \ mathbf {R} ^ {n} \ rightarrow \ mathbf {R} ^ {n}}$

macierz Jakobian jest macierzą n × n , której wpisy są podane przez pochodne cząstkowe

${\ Displaystyle D (f) = \ lewo ({\ Frac {\ częściowy f_ {i}} {\ częściowy x_ {j}}} \ prawej) _ {1 \ równoważnik ja, j \ równoważnik n}.}$

Jej wyznacznik, wyznacznik Jakobian , pojawia się w wyżej-wymiarowej wersji całkowania przez podstawienie : dla odpowiednich funkcji f i otwartego podzbioru U z R ⁿ (dziedzina f ), całka przez f ( U ) jakiejś innej funkcji φ  : R ⁿ → R ^m jest podane przez

${\ Displaystyle \ int _ {f (U)} \ phi (\ mathbf {v} ) \ d \ mathbf {v} = \ int _ {U} \ phi (f (\ mathbf {u}})) \ lewo |\det(\nazwa operatora {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .}$

Jakobian występuje również w twierdzeniu o funkcji odwrotnej .

Abstrakcyjne aspekty algebraiczne

Wyznacznik endomorfizmu

Powyższe tożsamości dotyczące wyznacznika iloczynów i odwrotności macierzy implikują, że macierze podobne mają ten sam wyznacznik: dwie macierze A i B są podobne, jeśli istnieje macierz odwracalna X taka, że A = X ⁻¹ BX . Rzeczywiście, wielokrotne stosowanie powyższych tożsamości daje

${\ Displaystyle \ det (A) = \ det (X) ^ {-1} \ det (B) \ det (X) = \ det (B) \ det (X) ^ {-1} \ det (X) =\det(B).}$

Wyznacznik nazywa się zatem również niezmiennikiem podobieństwa . Wyznacznik przekształcenia liniowego

${\displaystyle T:V\rightarrow V}$

dla pewnej skończenie wymiarowej przestrzeni wektorowej V jest zdefiniowana jako wyznacznik macierzy ją opisującej, ze względu na arbitralny wybór bazy w V . Przez niezmienność podobieństwa determinanta ta jest niezależna od wyboru bazy dla V, a zatem zależy tylko od endomorfizmu T .

Macierze kwadratowe nad pierścieniami przemiennymi

Powyższa definicja wyznacznika za pomocą reguły Leibniza sprawdza się ogólniej, gdy wpisy macierzy są elementami pierścienia przemiennego , takimi jak liczby całkowite , w przeciwieństwie do pola liczb rzeczywistych lub zespolonych. Co więcej, charakterystyka wyznacznika jako unikalnej przemiennej mapy wieloliniowej, która spełnia, nadal obowiązuje, podobnie jak wszystkie właściwości wynikające z tej charakterystyki. ${\ Displaystyle R}$${\ Displaystyle \ mathbf {Z}}$${\ Displaystyle \ Operatorname {det} (I) = 1}$

Macierz jest odwracalna (w tym sensie, że istnieje odwrotna macierz, której wpisy znajdują się w ) wtedy i tylko wtedy, gdy jej wyznacznikiem jest element odwracalny w . Dla , oznacza to, że wyznacznikiem jest +1 lub -1. Taka macierz nazywana jest unimodularną . ${\ Displaystyle A \ w \ operatorname {Mat} _ {n \ razy n} (R)}$${\ Displaystyle R}$${\ Displaystyle R}$${\ Displaystyle R = \ mathbf {Z}}$

Wyznacznik będący multiplikatywnym określa homomorfizm grupowy

${\ Displaystyle \ operatorname {GL} _ {n} (R) \ rightarrow R ^ {\ razy},}$

między ogólną grupą liniową (grupą macierzy odwracalnych z wpisami w ) a multiplikatywną grupą jednostek w . Ponieważ uwzględnia mnożenie w obu grupach, ta mapa jest homomorfizmem grup . ${\displaystyle n\razy n}$${\ Displaystyle R}$${\ Displaystyle R}$

Biorąc pod uwagę homomorfizm pierścienia , otrzymujemy mapę przez zastąpienie wszystkich wpisów w ich obrazami pod . Wyznacznik szanuje te mapy, tj. tożsamość ${\ Displaystyle f: R \ do S}$${\ Displaystyle \ operatorname {GL} _ {n} (f): \ operatorname {GL} _ {n} (R) \ do \ operatorname {GL} _ {n} (S)}$${\ Displaystyle R}$${\displaystyle f}$

${\ Displaystyle f (\ det ((a_ {i, j}))) = \ det ((f (a_ {i, j})))}$

trzyma. Innymi słowy, wyświetlany wykres przemienny przejeżdża.

Na przykład wyznacznikiem sprzężenia zespolonego macierzy zespolonej (która jest jednocześnie wyznacznikiem jej sprzężonej transpozycji) jest sprzężenie zespolone jej wyznacznika, a dla macierzy liczb całkowitych: moduł redukcji wyznacznika takiej macierzy jest równy wyznacznik macierzy zredukowany modulo (ten ostatni wyznacznik jest obliczany za pomocą arytmetyki modularnej ). W języku teorii kategorii wyznacznikiem jest naturalna transformacja między dwoma funktorami i . Dodając jeszcze jedną warstwę abstrakcji, jest to uchwycone przez stwierdzenie, że wyznacznikiem jest morfizm grup algebraicznych , od ogólnej grupy liniowej do grupy multiplikatywnej , ${\ Displaystyle m}$${\ Displaystyle m}$${\ Displaystyle \ Operatorname {GL} _ {n}}$${\ Displaystyle (-) ^ {\ razy}}$

${\ Displaystyle \ det: \ operatorname {GL} _ {n} \ rightarrow \ mathbb {G} _ {m}}.$

Algebra zewnętrzna

Wyznacznik liniowej transformacji wystąpienia wymiarowej przestrzeni wektorowej , lub, bardziej ogólnie wolne moduł z (Finite) stopnia na pierścienia przemiennego może być formułowany w sposób wolny od współrzędnych rozważając -tym zewnątrz siłę na . Mapa indukuje mapę liniową ${\displaystyle T:V\doV}$${\ Displaystyle n}$${\ Displaystyle V}$ ${\ Displaystyle n}$${\ Displaystyle R}$${\ Displaystyle n}$ ${\ Displaystyle \ bigwedge ^ {n} V}$${\ Displaystyle V}$${\displaystyle T}$

${\ Displaystyle {\ zacząć {wyrównany} \ bigwedge ^ {n} T: \ bigwedge ^ {n} V i \ rightarrow \ bigwedge ^ {n} V \ \ v_ {1} \ klin V_ {2} \ klin \ kropki \ wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}}$

Podobnie jak jednowymiarowa, mapa jest dana przez pomnożenie przez pewien skalar, tj. element w . Niektórzy autorzy, tacy jak ( Bourbaki 1998 ) wykorzystują ten fakt do zdefiniowania wyznacznika jako elementu spełniającego następującą tożsamość (dla wszystkich ): ${\ Displaystyle \ bigwedge ^ {n} V}$${\ Displaystyle \ bigwedge ^ {n} T}$${\ Displaystyle R}$${\ Displaystyle R}$${\ Displaystyle V_ {i} \ w V}$

${\ Displaystyle \ lewo (\ bigwedge ^ {n} T \ po prawej) \ lewo (V_ {1} \ klin \ kropki \ klin V_ {n} \ po prawej) = \ det (T) \ cdot v_ {1} \ klin \dots \wedge v_{n}.}$

Ta definicja jest zgodna z bardziej konkretną definicją zależną od współrzędnych. Można to pokazać za pomocą jedności wieloliniowej formy przemiennej na -krotkach wektorów w . Z tego powodu najwyższa niezerowa moc zewnętrzna (w przeciwieństwie do wyznacznika związanego z endomorfizmem) jest czasami nazywana wyznacznikiem i podobnie dla bardziej zaangażowanych obiektów, takich jak wiązki wektorowe lub kompleksy łańcuchowe przestrzeni wektorowych. W tym ustawieniu można również oddać elementy drugorzędne macierzy, biorąc pod uwagę niższe formy naprzemienne z . ${\ Displaystyle n}$${\ Displaystyle R ^ {n}}$${\ Displaystyle \ bigwedge ^ {n} V}$${\ Displaystyle V}$${\ Displaystyle \ bigwedge ^ {k} V}$${\displaystyle k<n}$

Uogólnienia i pojęcia pokrewne

Omówione powyżej determinanty dopuszczają kilka wariantów: jako wyznacznik definiuje się permanent macierzy, z tym że pomija się czynniki występujące w regule Leibniza. Immanant uogólnia zarówno poprzez wprowadzenie znaku z grupy symetrycznej w regule Leibniza. ${\displaystyle \operatorname {sgn}(\sigma)}$ ${\displaystyle S_{n}}$

Wyznaczniki algebr skończenie wymiarowych

Dla każdej algebry asocjacyjnej, która jest skończenie wymiarowa jako przestrzeń wektorowa nad ciałem , istnieje mapa determinantowa ${\ Displaystyle A}$${\ Displaystyle F}$

${\displaystyle \operatorname {det}:A\do F.}$

Definicja ta przebiega przez ustalenie wielomianu charakterystycznego niezależnie od wyznacznika i zdefiniowanie wyznacznika jako najniższego rzędu tego wielomianu. Ta ogólna definicja odzyskuje wyznacznik algebry macierzy , ale obejmuje również kilka innych przypadków , w tym wyznacznik kwaternion , ${\ Displaystyle A = \ nazwa operatora {Mat} _ {n \ razy n} (F)}$

${\ Displaystyle \ operatorname {det} (a + ib + jc + kd) = a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2}}$,

norma o rozszerzenie ciała , jak również Pfaffian o macierz antysymetryczna i zmniejszona norma o Algebra centralna prosta , powstają również szczególnych przypadkach tej konstrukcji. ${\ Displaystyle N_ {L/F}: L \ do F}$

Nieskończone macierze

W przypadku macierzy o nieskończonej liczbie wierszy i kolumn powyższe definicje wyznacznika nie są przenoszone bezpośrednio. Na przykład we wzorze Leibniza należałoby obliczyć nieskończoną sumę (której wszystkie wyrazy są iloczynami nieskończonymi). Analiza funkcjonalna dostarcza różnych rozszerzeń wyznacznika dla takich nieskończenie wymiarowych sytuacji, które jednak działają tylko dla określonych rodzajów operatorów.

Fredholm determinantą określa wyznacznik dla operatorów zwanych operatorów klasy ślad za pomocą odpowiedniego uogólnienie wzoru

${\displaystyle \det(I+A)=\exp(\operator {tr}(\log(I+A))).}$

Innym nieskończenie wymiarowym pojęciem wyznacznika jest wyznacznik funkcjonalny .

Operatory w algebrach von Neumanna

Dla operatorów w czynniku skończonym , można zdefiniować dodatni wyznacznik o wartościach rzeczywistych, zwany wyznacznikiem Fuglede-Kadisona, używając śladu kanonicznego. W rzeczywistości, każdemu stanowi śladowemu w algebrze von Neumanna odpowiada pojęcie wyznacznika Fuglede-Kadisona.

Pokrewne pojęcia dla nieprzemiennych pierścieni

W przypadku macierzy nad nieprzemiennymi pierścieniami właściwości wieloliniowości i przemienne są niekompatybilne dla n ≥ 2 , więc nie ma dobrej definicji wyznacznika w tym ustawieniu.

W przypadku macierzy kwadratowych z wpisami w pierścieniu nieprzemiennym występują różne trudności w definiowaniu wyznaczników analogicznie jak dla pierścieni przemiennych. Formuła Leibniza może mieć znaczenie pod warunkiem, że zostanie określona kolejność iloczynu i podobnie dla innych definicji wyznacznika, ale nieprzemienność prowadzi wówczas do utraty wielu podstawowych właściwości wyznacznika, takich jak własność multiplikatywna lub że wyznacznik pozostaje niezmieniony przy transpozycji macierzy. Nad non-pierścień przemienny, nie ma rozsądne pojęcie multilinear postaci (istnienie niezerową bilinear postaci z regularnym elementem z R jako wartości na jakiejś pary argumentów wynika, że R jest przemienne). Niemniej jednak sformułowano różne pojęcia wyznacznika nieprzemiennego, które zachowują niektóre właściwości wyznaczników, zwłaszcza quasideterminant i wyznacznik Dieudonné . Dla niektórych klas macierzy z elementami nieprzemiennymi można zdefiniować wyznacznik i udowodnić twierdzenia algebry liniowej, które są bardzo podobne do ich przemiennych analogów. Przykłady obejmują q -determinant na grupy kwantowej determinantę Capelli na macierzach Capellego i Berezinian na supermatrices (to znaczy macierzy, których prace są elementy - stopniowanych palników ). Macierze Manina tworzą klasę najbliższą macierzy z elementami przemiennymi. ${\ Displaystyle \ mathbb {Z} _ {2}}$

Obliczenie

Determinanty są wykorzystywane głównie jako narzędzie teoretyczne. Rzadko są obliczane wprost w numerycznej algebrze liniowej , gdzie w zastosowaniach takich jak sprawdzanie odwracalności i znajdowanie wartości własnych wyznacznik został w dużej mierze wyparty przez inne techniki. Geometria obliczeniowa często jednak korzysta z obliczeń związanych z wyznacznikami.

Podczas wyznacznik można wyznaczyć bezpośrednio z Leibniz wyklucza to podejście jest bardzo nieskuteczne dla dużej macierzy, ponieważ wzór wymaga obliczenia ( czynnikowe ) produktów na -Matrix. W ten sposób liczba wymaganych operacji rośnie bardzo szybko: to jest w porządku . Rozszerzenie Laplace'a jest podobnie nieefektywne. Dlatego opracowano bardziej zaangażowane techniki obliczania wyznaczników. ${\displaystyle n!}$${\ Displaystyle n}$ ${\displaystyle n\razy n}$ ${\displaystyle n!}$

Metody dekompozycji

Niektóre metody obliczają , zapisując macierz jako iloczyn macierzy, których wyznaczniki można łatwiej obliczyć. Takie techniki określane są jako metody dekompozycji. Przykłady obejmują metoda lu , w QR rozkładowi lub rozpadowi Cholesky'iego (na dodatnio określonych macierzy ). Metody te są uporządkowane , co stanowi znaczną poprawę . ${\ Displaystyle \ Operatorname {det} (A)}$${\ Displaystyle \ Operatorname {O} (n ^ {3})}$${\ Displaystyle \ Operatorname {O} (n!)}$

Na przykład dekompozycja LU wyraża się jako produkt ${\ Displaystyle A}$

${\ Displaystyle A = PLU.}$

z matrycy permutacji (który ma dokładnie jeden w każdej kolumnie, a inaczej zera), dolną matrycę trójkątnym i górnej trójkątnej matrycy . Wyznaczniki dwóch trójkątnych macierzy i można szybko oblicza, gdyż są produktami odpowiednimi wpisami przekątnej. Wyznacznikiem jest tylko znak odpowiedniej permutacji (co dotyczy parzystej liczby permutacji i nieparzystej liczby permutacji). Gdy znany jest taki rozkład LU dla , jego wyznacznik jest łatwo obliczany jako ${\displaystyle P}$${\ Displaystyle 1}$${\ Displaystyle L}$${\ Displaystyle U}$${\ Displaystyle L}$${\ Displaystyle U}$${\displaystyle P}$${\displaystyle \varepsilon}$${\displaystyle +1}$${\ Displaystyle -1}$${\ Displaystyle A}$

${\ Displaystyle \ det (A) = \ varepsilon \ det (L) \ cdot \ det (U).}$

Dalsze metody

Porządek osiągnięty metodami dekompozycji został poprawiony różnymi metodami. Jeśli dwie macierze porządku można pomnożyć w czasie , gdzie dla niektórych , to istnieje algorytm obliczający wyznacznik w czasie . Oznacza to na przykład, że istnieje algorytm oparty na algorytmie Coppersmitha–Winograda . Wykładnik ten został dodatkowo obniżony, począwszy od 2016 r., do 2,373. ${\ Displaystyle \ Operatorname {O} (n ^ {3})}$${\ Displaystyle n}$${\ Displaystyle M (n)}$${\ Displaystyle M (n) \ geq n ^ {a}}$${\displaystyle a>2}$${\ Displaystyle O (M (n))}$${\ Displaystyle \ Operatorname {O} (n ^ {2.376})}$

Oprócz złożoności algorytmu, do porównywania algorytmów można zastosować dalsze kryteria. Zwłaszcza w przypadku aplikacji dotyczących macierzy nad pierścieniami istnieją algorytmy obliczające wyznacznik bez żadnych dzieleń. (Z kolei eliminacja Gaussa wymaga podziałów.) Jeden z takich algorytmów, mający złożoność, opiera się na następującej idei: zastępujemy permutacje (jak w regule Leibniza) tzw. zamkniętymi spacerami uporządkowanymi , w których kilka pozycji może się powtarzać. Otrzymana suma ma więcej wyrazów niż w regule Leibniza, ale w tym procesie kilka z tych iloczynów może być ponownie użytych, co czyni ją bardziej wydajną niż naiwne obliczenia z regułą Leibniza. Algorytmy można również oceniać na podstawie ich złożoności bitowej , tj. ile bitów dokładności jest potrzebnych do przechowywania wartości pośrednich występujących w obliczeniach. Na przykład metoda eliminacji Gaussa (lub dekompozycji LU) jest uporządkowana , ale długość bitowa wartości pośrednich może stać się wykładniczo długa. Dla porównania, algorytm Bareiss jest metodą dokładnego dzielenia (więc używa dzielenia, ale tylko w przypadkach, gdy te podziały mogą być wykonane bez reszty) jest tej samej kolejności, ale złożoność bitowa jest z grubsza wielkością bitu oryginalne wpisy w czasach macierzy . ${\ Displaystyle \ Operatorname {O} (n ^ {4})}$${\ Displaystyle \ Operatorname {O} (n ^ {3})}$${\ Displaystyle n}$

Jeśli wyznacznik A i odwrotność A zostały już obliczone, lemat o wyznaczniku macierzy pozwala na szybkie obliczenie wyznacznika A + uv ^T , gdzie u i v są wektorami kolumnowymi.

Charles Dodgson (tj. Lewis Carroll z Alicji w Krainie Czarów ) wynalazł metodę obliczania wyznaczników zwaną kondensacją Dodgsona . Niestety ta ciekawa metoda nie zawsze działa w swojej pierwotnej formie.

Zobacz też

Uwagi

Bibliografia

• Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
• Osra, Sheldona Jaya (2015). Algebra liniowa zrobione w prawo (3rd ed.). Springer . Numer ISBN 978-3-319-11079-0.
• Bareiss, Erwin (1968), "Tożsamość Sylvestera i wielostopniowa eliminacja Gaussa z zachowaniem liczby całkowitej" (PDF) , Matematyka obliczeń , 22 (102): 565-578, doi : 10.2307/2004533 , JSTOR  2004533
• de Boor, Carl (1990), "Puste ćwiczenie" (PDF) , Biuletyn ACM SIGNUM , 25 (2): 3-7, doi : 10.1145/122272.122273 , S2CID  62780452
• Bourbaki, Nicolas (1998), Algebra I, rozdziały 1-3 , Springer, ISBN 9783540642435
• Pęczek, JR; Hopcroft, JE (1974). „Trójkątna faktoryzacja i odwracanie przez szybkie mnożenie macierzy” . Matematyka Obliczeń . 28 (125): 231-236. doi : 10.1090/S0025-5718-1974-0331751-8 .
• Dummit, David S.; Foote, Richard M. (2004), Abstrakcyjna algebra (3rd ed.), Hoboken, NJ: Wiley, ISBN 9780471452348, OCLC  248917264
• Fisikopoulos, Wissarion; Peñaranda, Luis (2016), "Szybsze algorytmy geometryczne poprzez dynamiczne obliczanie wyznaczników", Geometria obliczeniowa , 54 : 1-16, doi : 10.1016/j.comgeo.2015.12.001
• Garibaldi, Skip (2004), „Wielomian charakterystyczny i wyznacznik nie są konstrukcjami ad hoc”, American Mathematical Monthly , 111 (9): 761-778, arXiv : math/0203276 , doi : 10.2307/4145188 , JSTOR  4145188 , MR  2104048
• Habgood, Ken; Arel, Itamar (2012). „Oparte na kondensacji zastosowanie zasady Cramera do rozwiązywania wielkoskalowych układów liniowych” (PDF) . Dziennik algorytmów dyskretnych . 10 : 98–109. doi : 10.1016/j.jda.2011.06.007 .
• Harris, Frank E. (2014), Matematyka dla nauk fizycznych i inżynierii , Elsevier, ISBN 9780128010495
• Kleiner, Izrael (2007), Kleiner, Izrael (red.), Historia algebry abstrakcyjnej , Birkhäuser, doi : 10.1007/978-0-8176-4685-1 , ISBN 978-0-8176-4684-4, MR  2347309
• Kung, Józef PS; Rota, Gian-Carlo; Yan, Catherine (2009), Kombinatoryka: The Rota Way , Cambridge University Press, ISBN 9780521883894
• Lay, David C. (22 sierpnia 2005), Algebra liniowa i jej zastosowania (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
• Lombardi, Henryk; Quitté, Claude (2015), Algebra przemienna: metody konstrukcyjne , Springer, ISBN 9789401799447
• Mac Lane, Saunders (1998), Categories for the Working Mathematician , Graduate Texts in Mathematics 5 (wyd. 2), Springer-Verlag, ISBN 0-387-98403-8
• Meyer, Carl D. (15 lutego 2001), Analiza macierzowa i stosowana algebra liniowa , Towarzystwo Matematyki Przemysłowej i Stosowanej (SIAM), ISBN 978-0-89871-454-8, zarchiwizowane od oryginału w dniu 31.10.2009
• Muir, Thomas (1960) [1933], Traktat o teorii wyznaczników , poprawione i rozszerzone przez Williama H. ​​Metzlera, New York, NY: Dover
• Poole, David (2006), Algebra Liniowa: Nowoczesne Wprowadzenie (2nd ed.), Brooks / Cole, ISBN 0-534-99845-3
• G. Baley Price (1947) „Niektóre tożsamości w teorii wyznaczników”, American Mathematical Monthly 54:75-90 MR 0019078
• Róg, Roger Alan ; Johnson, Charles Royal (2018) (1985). Analiza macierzy (wyd. 2). Wydawnictwo Uniwersytetu Cambridge . Numer ISBN 978-0-521-54823-6.
• Lang, Serge (1985), Wprowadzenie do algebry liniowej , Teksty licencjackie z matematyki (2 wyd.), Springer, ISBN 9780387962054
• Lang, Serge (1987), Algebra Liniowa , Teksty licencjackie z matematyki (3 wyd.), Springer, ISBN 9780387964126
• Lang, Serge (2002). Algebra . Teksty magisterskie z matematyki. Nowy Jork, NY: Springer. Numer ISBN 978-0-387-95385-4.
• Leon, Steven J. (2006), Algebra liniowa z aplikacjami (7th ed.), Pearson Prentice Hall
• Rote, Günter (2001), "Algorytmy bez podziałów dla wyznacznika i Pfaffiana: podejścia algebraiczne i kombinatoryczne" (PDF) , Obliczeniowa matematyka dyskretna , Notatki do wykładu z obliczeń. Sci., 2122 , Springer, s. 119-135, doi : 10.1007/3-540-45506-X_9 , MR  1911585
• Trefethen, Lloyd; Bau III, David (1997), Numeryczna Algebra Liniowa (1st ed.), Filadelfia: SIAM, ISBN 978-0-89871-361-9

odniesienia historyczne

• Bourbaki, Nicolas (1994), Elementy historii matematyki , przekład Meldrum, John, Springer, doi : 10.1007/978-3-642-61693-8 , ISBN 3-540-19376-6
• Cajori, Florian (1993), Historia notacji matematycznych: W tym tom. I. Notacje w matematyce elementarnej; Tom. II. Zapisy głównie w matematyce wyższej, Przedruk oryginałów z 1928 i 1929 r. , Dover, ISBN 0-486-67766-4, MR  3363427
• Bezout, Étienne (1779), Théorie générale des równań algébriques , Paryż
• Cayley, Arthur (1841), "O twierdzeniu o geometrii położenia", Cambridge Mathematical Journal , 2 : 267-271
• Cramer, Gabriel (1750), Wprowadzenie do analizy des lignes courbes algébriques , Genève: Frères Cramer & Cl. Philibert, doi : 10.3931/e-rara-4048
• Eves, Howard (1990), Wprowadzenie do historii matematyki (6 wyd.), Saunders College Publishing, ISBN 0-03-029558-0, MR  1104435
• Grattan-Guinness, I., wyd. (2003), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences , 1 , Johns Hopkins University Press , ISBN 9780801873966
• Jacobi, Carl Gustav Jakob (1841), „Determinantibus functionibus” , Journal für die reine und angewandte Mathematik , 1841 (22): 320-359, doi : 10.1515/crll.1841.22.319 , S2CID  123637858
• Laplace, Pierre-Simon, de (1772), „Recherches sur le calcul intégral et sur le systéme du monde” , Histoire de l'Académie Royale des Sciences , Paryż (partie druga): 267-376

Zewnętrzne linki

• Suprunenko, DA (2001) [1994], "Determinant" , Encyklopedia Matematyki , EMS Press
• Weisstein, Eric W. „Wyznacznik” . MatematykaŚwiat .
• O'Connor, John J .; Robertson, Edmund F. , „Macierze i wyznaczniki” , archiwum historii matematyki MacTutor , University of St Andrews
• Determinant Interaktywny program i samouczek
• Algebra liniowa: wyznaczniki. Oblicz wyznaczniki macierzy do rzędu 6 za pomocą wybranego przez siebie rozszerzenia Laplace'a.
• Macierze i algebra liniowa na stronach najwcześniej używanych
• Determinanty wyjaśnione w łatwy sposób w 4 rozdziale w ramach kursu algebry liniowej.