Grupa modułowa - Modular group

Struktura algebraiczna → Teoria grup Teoria grup
Podstawowe pojęcia Podgrupa Podgrupa normalna Grupa ilorazowa (Pół) bezpośredni produkt Homomorfizmy grupowe jądro wizerunek suma bezpośrednia produkt wieniec prosty skończone nieskończony ciągły mnożny przyłączeniowy cykliczny abelian dwuścienny nilpotentny rozpuszczalny akcja Słowniczek teorii grup Lista tematów teorii grup
Grupy skończone Klasyfikacja skończonych grup prostych cykliczny zmienny Typ kłamstwa sporadyczny Twierdzenie Cauchy'ego Twierdzenie Lagrange'a Twierdzenia Sylowa Twierdzenie Halla grupa p Podstawowa grupa abelowa Grupa Frobenius Mnożnik Schura Grupa symetryczna S n Klein czterogrupa V Grupa dwuścienna D n Quaternion grupa Q Grupa dicykliczna Dic n
Dyskretne grupy Kraty Liczby całkowite ( )${\ Displaystyle \ mathbb {Z}}$ Bezpłatna grupa Grupy modułowe PSL(2, )${\ Displaystyle \ mathbb {Z}}$ SL(2, )${\ Displaystyle \ mathbb {Z}}$ Grupa arytmetyczna Krata Grupa hiperboliczna
Grupy topologiczne i Liego Elektrozawór okrąg Ogólne liniowe GL( n ) Specjalne liniowe SL( n ) Ortogonalny O( n ) Euklidesa E( n ) Specjalne ortogonalne SO( n ) Jednostkowe U ( n ) Specjalna jednostkowa SU( n ) Symplektyczny Sp ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Konformalne Dyfeomorfizm Pętla Nieskończenie wymiarowa grupa Liego O(∞) SU(∞) Sp(∞)
Grupy algebraiczne Liniowa grupa algebraiczna Grupa redukcyjna Odmiana abelowa Krzywa eliptyczna
v t mi

W matematyce The grupy modułowej jest rzutowa specjalny liniową grupę PSL (2, Z ), z 2 x 2 matryc z całkowitych współczynników i determinanty 1. matryc i - zidentyfikowane. Grupa modularna działa na górnej połowie płaszczyzny zespolonej przez ułamkowe przekształcenia liniowe , a nazwa „grupa modularna” pochodzi od relacji do przestrzeni moduli, a nie od arytmetyki modularnej .

Definicja

Modułowy zespół Γ jest grupa o liniowej transformacji ułamkową w górnej połowie płaszczyzny zespolonej , która ma postać

${\ Displaystyle Z \ mapsto {\ Frac {az + b} {cz + d}}}$

gdzie a , b , c , d są liczbami całkowitymi, a ad − bc = 1 . Operacja grupowa to kompozycja funkcji .

Ta grupa przekształceń jest izomorficzna z rzutową specjalną grupą liniową PSL(2, Z ) , która jest ilorazem dwuwymiarowej specjalnej grupy liniowej SL(2, Z ) przez liczby całkowite przez jej środek { I , − I } . Innymi słowy, PSL(2, Z ) składa się ze wszystkich macierzy

${\displaystyle {\zacząć{pmatrix}a&b\\c&d\koniec{pmatrix}}}$

gdzie a , b , c , d są liczbami całkowitymi, ad − bc = 1 , a pary macierzy A i − A są uważane za identyczne. Operacja grupowa to zwykłe mnożenie macierzy .

Niektórzy autorzy definiują grupę modularną jako PSL(2, Z ) , a jeszcze inni definiują grupę modularną jako większą grupę SL(2, Z ) .

Niektóre zależności matematyczne wymagają uwzględnienia grupy GL(2, Z ) macierzy z wyznacznikiem plus lub minus jeden. ( SL(2, Z ) jest podgrupą tej grupy.) Podobnie, PGL(2, Z ) jest grupą ilorazową GL(2, Z )/{ I , − I } . 2 x 2 macierz jednostkową determinantą jest symplektycznych matrycy , a tym samym SL (2, Z ) = SP (2, Z ) The symplektycznych grupy od 2 x 2 matryce.

Znajdowanie elementów

Aby znaleźć jawne elementy w SL(2, Z ) , jest sztuczka polegająca na wzięciu dwóch względnie pierwszych liczb całkowitych , wstawieniu ich do macierzy${\displaystyle a,b}$

${\displaystyle {\zacząć{pmatrix}a&x\\b&y\koniec{pmatrix}}}$

i rozwiązywanie równania wyznacznika

${\displaystyle ay-bx=1}$

Zauważ wyznacznik siły równanie być względnie pierwsze, ponieważ w przeciwnym razie nie byłoby czynnikiem takie, że , stąd${\displaystyle a,b}$${\displaystyle c}$${\displaystyle ca'=a}$${\displaystyle cb'=b}$

${\displaystyle c(a'y-b'x)=1}$

nie miałby rozwiązań całkowitoliczbowych. Na przykład, jeśli wtedy równanie wyznaczające brzmi:${\ Displaystyle a = 7, {\ tekst {}} b = 6}$

${\ Displaystyle 7y-6x = 1}$

następnie bierze i daje , stąd${\displaystyle y=-5}$${\displaystyle x=-6}$${\ Displaystyle -35-(-36) = 1}$

${\ Displaystyle {\ zacząć {pmatrix} 7 i 6 \ \ 6 i 5 \ koniec {pmatrix}}}$

jest macierzą. Następnie za pomocą rzutowania macierze te definiują elementy w PSL(2, Z ) .

Własności teoretyczne liczb

Wyznacznik jednostkowy

${\displaystyle {\zacząć{pmatrix}a&b\\c&d\koniec{pmatrix}}}$

oznacza, że ​​ułamki _za/b, _za/do, _do/re, _b/rewszystkie są nieredukowalne, czyli nie mają wspólnych czynników (oczywiście pod warunkiem, że mianowniki są niezerowe). Bardziej ogólnie, jeślip/q jest ułamkiem nieredukowalnym, więc

${\displaystyle {\frac {ap+bq}{cp+dq}}}$

jest również nieredukowalna (ponownie, pod warunkiem, że mianownik jest niezerowy). W ten sposób można połączyć dowolną parę ułamków nieredukowalnych; to znaczy dla dowolnej paryp/q i r/s ułamków nieredukowalnych istnieją pierwiastki

${\ Displaystyle {\ zacząć {pmatrix} a & b \ \ c i d \ koniec {pmatrix}} \ w \ operatorname {SL} (2 \ mathbf {Z})}$

takie, że

${\displaystyle r=ap+bq\quad {\mbox{i}}\quad s=cp+dq.}$

Elementy grupy modułowej zapewniają symetrię na siatce dwuwymiarowej . Niech ω ₁ i ω ₂ będą dwiema liczbami zespolonymi, których stosunek nie jest rzeczywisty. Następnie zbiór punktów

${\ Displaystyle \ Lambda (\ omega _ {1} \ omega _ {2}) = \ { m \ omega _ {1} + n \ omega _ {2}: m, n \ w \ mathbf {Z} \ }}$

jest siecią równoległoboków na płaszczyźnie. Inna para wektorów α ₁ i α ₂ wygeneruje dokładnie tę samą sieć wtedy i tylko wtedy, gdy

${\ Displaystyle {\ zacząć {pmatrix} \ alfa _ {1} \ \ \ alfa _ {2} \ koniec {pmatrix}} = {\ zacząć {pmatrix} a & b \ \ c i d \ koniec {pmatrix}} {\ zacząć { pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}}}$

dla jakiejś macierzy w GL(2, Z ) . Z tego powodu funkcje podwójnie okresowe , takie jak funkcje eliptyczne , posiadają symetrię grupy modularnej.

Działanie grupy modularnej na liczby wymierne można najłatwiej zrozumieć, wyobrażając sobie siatkę kwadratową, w której punkt siatki ( p , q ) odpowiada ułamkowip/q(patrz sad Euklidesa ). Frakcja nieredukowalna to taka, która jest widoczna od początku; działanie grupy modularnej na ułamku nigdy nie zmienia widzialnego (nieredukowalnego) w ukryte (redukowalne) i vice versa.

Zauważ, że każdy członek grupy modularnej odwzorowuje projekcyjnie rozszerzoną linię rzeczywistą jeden do jednego na siebie, a ponadto w sposób bijective odwzorowuje projekcyjnie rozszerzoną prostą wymierną (wymierne z nieskończonością) na siebie, niewymierne na niewymierne, liczby transcendentalne na liczby przestępne, liczby nierzeczywiste do liczb nierzeczywistych, górna półpłaszczyzna do górnej półpłaszczyzny i tak dalej.

Gdyby p _{n- 1}/q _{n −1} i p _n/q _nto dwie kolejne zbieżności ułamka łańcuchowego , to macierz

${\ Displaystyle {\ zacząć {pmatrix} p_ {n-1} i p_ {n} \ \ q_ {n-1} i q_ {n} \ koniec {pmatrix}}}$

należy do GL(2, Z ) . W szczególności, jeśli bc − ad = 1 dla dodatnich liczb całkowitych a , b , c , d z a < b i c < d wtedyza/b i do/rebędą sąsiadami w sekwencji Fareya rzędu max( b , d ) . Ważnymi szczególnymi przypadkami zbieżności ułamków ciągłych są liczby Fibonacciego i rozwiązania równania Pella . W obu przypadkach liczby mogą być ustawione tak, aby utworzyć podzbiór półgrupy grupy modułowej.

Własności teorii grup

Prezentacja

Można pokazać, że grupa modułowa jest generowana przez dwie transformacje

${\ Displaystyle {\ zacząć {wyrównane} S i: z \ mapsto - {\ Frac {1} {z}} \ \ T i: z \ mapsto z + 1 \ koniec {wyrównane}}}$

tak, aby każdy element w grupie modularnej mógł być reprezentowany (w niejednoznaczny sposób) przez złożenie potęg S i T . Geometrycznie, S reprezentuje odwrócenie w okręgu jednostkowym, po którym następuje odbicie względem urojonej osi, podczas gdy T reprezentuje przesunięcie jednostki w prawo.

Generatory S i T zachowują relacje S ² = 1 i ( ST ) ³ = 1 . Można wykazać, że są to kompletne zestawy relacji, więc grupa modułowa ma prezentację :

${\ Displaystyle \ Gamma \ cong \ lewo \ langle S, T \ mid S ^ {2} = ja \ lewo (ST \ prawy) ^ {3} = ja \ prawy \ rangle}$

Ta prezentacja opisuje grupę modularną jako obrotową grupę trójkątów D(2, 3, ∞) (nieskończoność ponieważ nie ma relacji na T ), a zatem odwzorowuje się na wszystkie grupy trójkątów (2, 3, n ) przez dodanie relacji T ⁿ = 1 , który występuje np. w podgrupie kongruencji Γ( n ) .

Za pomocą generatorów S i ST zamiast S i T , przedstawiono, że grupa modułowych izomorficzne z wolnego produktu z cyklicznych grup C ₂ oraz C ₃ :

${\ Displaystyle \ Gamma \ cong C_ {2} * C_ {3}}$

• 

  Działanie T  : z ↦ z + 1 na H

• 

  Działanie S  : z ↦ −1/zna H

Grupa plecionek

Grupa oplotów B ₃ jest uniwersalnym centralnym przedłużeniem grupy modułowej, która jako kratownica znajduje się wewnątrz (topologicznej) uniwersalnej grupy osłonowej SL ₂ ( R ) → PSL ₂ ( R ) . Ponadto, grupa modułowa ma trywialne centrum, a tym samym zespół modułowy jest izomorficzny z grupy iloraz z B, ₃ modulo jego centrum ; równoważnie do grupy wewnętrznych automorfizmy z B, ₃ .

Grupa warkocz B ₃ z kolei jest izomorficzna z grupą węzłów z węzłem koniczyny .

Iloraz

Istotnym zainteresowaniem cieszą się ilorazowe podgrupy kongruencji.

Innymi ważnymi ilorazami są grupy trójkątów (2, 3, n ) , które odpowiadają geometrycznie opadaniu do walca, iloraz współrzędnej x modulo n , jako T ⁿ = ( z ↦ z + n ) . (2, 3, 5) to grupa symetrii dwudziestościennej , a grupa trójkątów (2, 3, 7) (i powiązane płytki) to pokrycie wszystkich powierzchni Hurwitz .

Prezentacja jako grupa macierzowa

Grupa może być generowana przez dwie macierze ${\ Displaystyle {\ tekst {SL}} _ {2} (\ mathbb {Z})}$

${\ Displaystyle S = {\ zacząć {pmatrix} 0 i 1 \ \ 1 i 0 \ koniec {pmatrix}}, {\ tekst {}} T = {\ zacząć {pmatrix} 1 i 1 \ \ 0 i 1 \ koniec {pmatrix}}}$

od

${\ Displaystyle S ^ {2} = - I_ {2} {\ tekst {}} (ST) ^ {3} = {\ zacząć {pmatrix} 0 i 1 \ \ 1 i 1 \ koniec {pmatrix}} ^ {3 }=-I_{2}}$

Projekcja zamienia te macierze w generatory , o relacjach zbliżonych do prezentacji grupowej. ${\ Displaystyle {\ tekst {SL}} _ {2} (\ mathbb {Z} ) \ do {\ tekst {PSL}} _ {2} (\ mathbb {Z} )}$${\ Displaystyle {\ tekst {PSL}} _ {2} (\ mathbb {Z})}$

Związek z geometrią hiperboliczną

Grupa modułowa jest istotna, ponieważ stanowi podgrupę z grupy izometryczne o hiperbolicznej płaszczyźnie . Jeśli wziąć pod uwagę górnej półpłaszczyźnie modelu H hiperboli płaskiej geometrii, to grupa wszystkich orientacji zabezpieczonego izometrii H obejmuje wszystkie transformacje MöBIUS formularza

${\ Displaystyle Z \ mapsto {\ Frac {az + b} {cz + d}}}$

gdzie a , b , c , d są liczbami rzeczywistymi . Pod względem współrzędnych rzutowych grupa PSL(2, R ) oddziałuje na górną półpłaszczyznę H przez rzutowość:

${\ Displaystyle [z, \ 1] {\ zacząć {pmatrix} a & c \ \ b i d \ koniec {pmatrix}} \ = \ [az + b, \ cz + d] \ \ grubościk \ \ lewo [{ \frac {az+b}{cz+d}},\ 1\prawo].}$

To działanie jest wierne . Ponieważ PSL(2, Z ) jest podgrupą PSL(2, R ) , grupa modularna jest podgrupą grupy izometrii H zachowujących orientację .

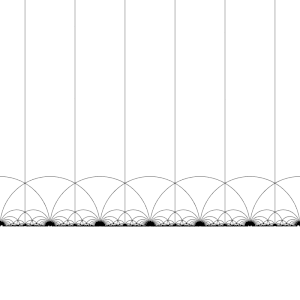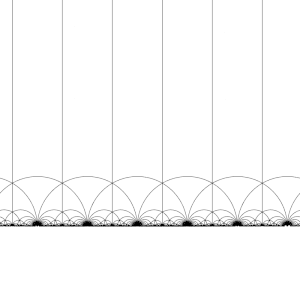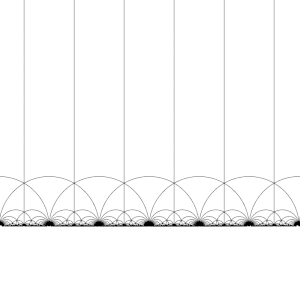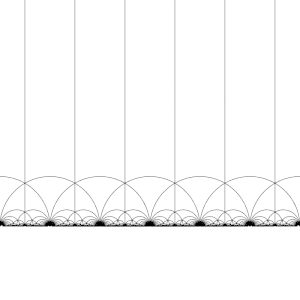
Teselacja płaszczyzny hiperbolicznej

Modułowa grupa Γ działa na H jako dyskretne podgrupy z PSL (2, R ) , to jest dla każdego Z w H można znaleźć sąsiedztwie Z , która nie zawiera żadnego innego elementu, na orbicie z Z . To oznacza również, że można skonstruować podstawowych dziedzin , które (w przybliżeniu) zawierają dokładnie jednego przedstawiciela każdej orbicie Z w H . (Potrzebna jest opieka na granicy domeny.)

Istnieje wiele sposobów konstruowania podstawowej domeny, ale powszechnym wyborem jest region

${\ Displaystyle R = \ lewo \ {z \ w \ mathbf {H} \ dwukropek \ lewo | z \ prawo | > 1 \ \ lewo | \ {\ mbox {Re}} (z) \ \ prawo |<{\tfrac {1}{2}}\right\}}$

ograniczone pionowymi liniami Re( z ) =1/2i Re( z ) = −1/2, a okrąg | z | = 1 . Ten region jest trójkątem hiperbolicznym. Ma wierzchołki w1/2+ ja√ 3/2i −1/2+ ja√ 3/2, gdzie kąt między jego bokami wynosi π/3, a trzeci wierzchołek w nieskończoności, gdzie kąt między jego bokami wynosi 0.

Przekształcając ten region kolejno przez każdy z elementów grupy modułowej, tworzona jest regularna teselacja płaszczyzny hiperbolicznej przez przystające trójkąty hiperboliczne, znane jako V6.6.∞ Trójkątne kafelki nieskończonego rzędu . Zauważ, że każdy taki trójkąt ma jeden wierzchołek w nieskończoności lub na osi rzeczywistej Im( z ) = 0 . To kafelkowanie można rozszerzyć na dysk Poincaré , gdzie każdy trójkąt hiperboliczny ma jeden wierzchołek na granicy dysku. Kafelkowanie dysku Poincarégo jest dane w naturalny sposób przez niezmiennik J , który jest niezmienny w grupie modularnej i osiąga każdą liczbę zespoloną raz w każdym trójkącie tych obszarów.

Teselację można nieco udoskonalić, dzieląc każdy region na dwie połowy (zwykle pokolorowane na czarno i biało), dodając mapę odwrócenia orientacji; kolory odpowiadają wtedy orientacji domeny. Dodanie ( x , y ) ↦ (− x , y ) i pobranie prawej połowy obszaru R (gdzie Re( z ) ≥ 0 ) daje zwykłą teselację. Teselacja ta pojawia się po raz pierwszy w druku w ( Klein i 1878/79a ), gdzie przypisuje się ją Richardowi Dedekindowi , w odniesieniu do ( Dedekind 1877 ).

Mapę grup (2, 3, ∞) → (2, 3, n ) (od grupy modułowej do grupy trójkątnej) można zwizualizować pod kątem tego kafelkowania (uzyskującego kafelkowanie na krzywej modułowej), jak pokazano na filmie po prawej.

Parakompaktowe płytki jednolite z rodziny [∞,3] v t mi
Symetria: [∞,3], (*∞32)							[∞,3] + (∞32)	[1 + ,∞,3] (*∞33)		[∞,3 + ] (3*∞)
		=	=	=				= lub	= lub	=
{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h 2 {∞,3}	s{3,∞}
Jednolite podwójne
V∞ 3	V3.∞.∞	V(3.∞) 2	V6.6.∞	V3 ∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞) 3		V3.3.3.3.3.∞

Podgrupy kongruencji

Ważne podgrupy grupy modułowej Γ , zwane podgrupami kongruencji , są wyznaczane przez nałożenie relacji kongruencji na powiązane macierze.

Istnieje naturalny homomorfizm SL(2, Z ) → SL(2, Z / N Z ) podany przez zredukowanie wpisów modulo N . Powoduje to homomorfizm na grupie modułowej PSL(2, Z ) → PSL(2, Z / N Z ) . Jądro tego homomorfizmu nazywany jest głównym zbieżność podgrupa z poziomu N , oznaczono Γ ( N ) . Mamy następującą krótką dokładną sekwencję :

${\ Displaystyle 1 \ do \ Gamma (N) \ do \ Gamma \ do {\ mbox {PSL}} (2, \ mathbf {Z} / N \ mathbf {Z}) \ do 1}$.

Będąc jądrem homomorfizmu Γ( N ) jest normalną podgrupą grupy modularnej Γ . Grupa Γ( N ) jest podana jako zbiór wszystkich przekształceń modularnych

${\ Displaystyle Z \ mapsto {\ Frac {az + b} {cz + d}}}$

dla których ≡ d ≡ ± 1 (mod N ) i b ≡ c ≡ 0 (mod N ) .

Łatwo wykazać, że ślad macierzy reprezentujący element Γ( N ) nie może mieć wartości −1, 0 lub 1, więc te podgrupy są grupami nieskręcanymi . (Istnieją inne podgrupy wolne od skręcania).

Główna podgrupa kongruencji poziomu 2, Γ(2) , jest również nazywana grupą modułową Λ . Ponieważ PSL(2, Z /2 Z ) jest izomorficzny z S ₃ , Λ jest podgrupą o indeksie 6. Grupa Λ składa się ze wszystkich przekształceń modularnych, dla których a i d są nieparzyste, a b i c są parzyste.

Inną ważną rodziną podgrup kongruencji jest grupa modularna Γ ₀ ( N ) zdefiniowana jako zbiór wszystkich przekształceń modularnych, dla których c ≡ 0 (mod N ) lub równoważnie, jako podgrupa, której macierze stają się górne trójkątne po redukcji modulo N . Należy zauważyć, że Γ ( N ) jest podgrupa y ₀ ( N ) . Te krzywe modułowe związane z tymi grupami są aspektem monstrualnej rojenia - dla głównego liczba p , modułowa krzywa normalizer jest rodzaj zera tylko wtedy, gdy p dzieli zamówienie z grupy potworów , albo równoważnie, gdy p jest supersingular pierwszy .

monoid dwójkowy

Jednym z ważnych podzbiorów grupy modularnej jest monoid dwuczłonowy , który jest monoidem wszystkich łańcuchów postaci ST ^k ST ^m ST ⁿ ... dla liczb całkowitych dodatnich k , m , n ,... . Ten monoid występuje naturalnie w badaniu krzywe fraktalne i opisuje samopodobieństwa symetrie z funkcji Cantora , funkcja Minkowskiego znakiem zapytania , a śniegu Koch , każdy jest szczególnym przypadkiem ogólnego de Rham krzywej . Monoid ma również reprezentacje liniowe w wyższych wymiarach; na przykład, reprezentacja N = 3 może być rozumiana jako opis samosymetrii krzywej Blancmange'a .

Mapy torusa

Grupa GL(2, Z ) to mapy liniowe zachowujące standardową sieć Z ² , a SL(2, Z ) to mapy zachowujące orientację zachowujące tę sieć; one zatem schodzić do samodzielnej homeomorfizmów z torusa (SL odwzorowywania map orientacji, zachowanie), aw rzeczywistości mapie izomorficznie do (Extended) odwzorowania klasy grupy torusa, co oznacza, że każdy z własnym homeomorfizm torusa jest izotopowy do A mapa tego formularza. Własności algebraiczne macierzy jako elementu GL(2, Z ) odpowiadają dynamice indukowanej mapy torusa.

Grupy Heckego

Grupę modułową można uogólnić na grupy Hecke , nazwane na cześć Ericha Hecke , i zdefiniować w następujący sposób.

Grupa Heckego H _q z q ≥ 3 , jest grupą dyskretną generowaną przez

${\ Displaystyle {\ zacząć {wyrównane} z i \ mapsto - {\ Frac {1} {z}} \ \ z i \ mapsto z + \ lambda _ {q} \ koniec {wyrównane}}}$

gdzie λ _q = 2 cosπ/q. Dla małych wartości q ≥ 3 , mamy:

${\ Displaystyle {\ zacząć {wyrównany} \ lambda _ {3} i = 1, \ \ \ lambda _ {4} i = {\ sqrt {2}}, \ \ \ lambda _ {5} i = {\ Frac {1+{\sqrt {5}}}{2}},\\\lambda _{6}&={\sqrt {3}},\\\lambda _{8}&={\sqrt {2+ {\sqrt {2}}}}.\end{wyrównany}}}$

Modułowa grupa Γ jest izomorficzny H ₃ i mają one właściwości i zastosowań - na przykład tak, jak ma się wolny produkt z grupy cyklicznych

${\ Displaystyle \ Gamma \ cong C_ {2} * C_ {3},}$

ogólniej ma

${\ Displaystyle H_ {q} \ cong C_ {2} * C_ {q}}$

co odpowiada grupie trójkątów (2, q , ∞) . Podobnie istnieje pojęcie głównych podgrup kongruencji związanych z głównymi ideałami w Z [ λ ] .

Historia

Grupa modularna i jej podgrupy zostały po raz pierwszy szczegółowo zbadane przez Richarda Dedekinda i Felixa Kleina w ramach jego programu Erlangen w latach 70. XIX wieku. Jednak blisko spokrewnione funkcje eliptyczne zostały zbadane przez Josepha Louisa Lagrange'a w 1785 roku, a dalsze wyniki dotyczące funkcji eliptycznych opublikowali Carl Gustav Jakob Jacobi i Niels Henrik Abel w 1827 roku.

Zobacz też

Bibliografia