Twierdzenia o izomorfizmie - Isomorphism theorems

W matematyce , a konkretnie algebrze abstrakcyjnej , twierdzenia o izomorfizmie (znane również jako twierdzenia o izomorfizmie Noether ) są twierdzeniami, które opisują związek między ilorazami , homomorfizmami i podobiektami . Istnieją wersje twierdzeń dla grup , pierścieni , przestrzeni wektorowych , modułów , algebr Liego i różnych innych struktur algebraicznych . W algebrze uniwersalnej twierdzenia o izomorfizmie można uogólnić na kontekst algebr ikongruencje .

Historia

Twierdzenia o izomorfizmie zostały sformułowane w pewnym ogólności dla homomorfizmów modułów przez Emmy Noether w jej artykule Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern , który został opublikowany w 1927 w Mathematische Annalen . Mniej ogólne wersje tych twierdzeń można znaleźć w pracach Richarda Dedekinda i wcześniejszych pracach Noether.

Trzy lata później BL van der Waerden opublikował swój wpływowy Moderne Algebra, pierwszy abstrakcyjny podręcznik do algebry, który uwzględniał podejście grup - pierścieni - pól do tematu. Van der Waerden przypisał wykłady Noether z teorii grup i Emila Artina z algebry, a także seminarium prowadzone przez Artina, Wilhelma Blaschke , Otto Schreiera i samego van der Waerdena na temat ideałów . Trzy twierdzenia o izomorfizmie, zwane twierdzeniem homomorfizmu , oraz dwa prawa izomorfizmu w przypadku zastosowania do grup, pojawiają się wyraźnie.

Grupy

Najpierw przedstawiamy twierdzenia o izomorfizmie grup .

Uwaga o numerach i nazwiskach

Poniżej przedstawiamy cztery twierdzenia, oznaczone jako A, B, C i D. Często są one numerowane jako „Pierwsze twierdzenie o izomorfizmie”, „Drugie...” i tak dalej; jednak nie ma powszechnej zgody co do numeracji. Tutaj podajemy kilka przykładów twierdzeń o izomorfizmie grup w literaturze. Zauważ, że te twierdzenia mają odpowiedniki dla pierścieni i modułów.

Porównanie nazw twierdzeń o izomorfizmie grup

	Autor	Twierdzenie A	Twierdzenie B	Twierdzenie C
Brak „trzeciego” twierdzenia	Jacobson	Podstawowe twierdzenie homomorfizmów	(drugie twierdzenie o izomorfizmie)	" często nazywany pierwszym twierdzeniem o izomorfizmie "
	van der Waerden, Durbin	Podstawowe twierdzenie homomorfizmów	pierwsze twierdzenie o izomorfizmie	drugie twierdzenie o izomorfizmie
	Knapp	(bez nazwy)	Drugie twierdzenie o izomorfizmie	Pierwsze twierdzenie o izomorfizmie
	Grille	Twierdzenie o homomorfizmie	Drugie twierdzenie o izomorfizmie	Pierwsze twierdzenie o izomorfizmie
Trzy ponumerowane twierdzenia	(Inna konwencja wymieniona w Grillet)	Pierwsze twierdzenie o izomorfizmie	Trzecie twierdzenie o izomorfizmie	Drugie twierdzenie o izomorfizmie
	Rotman	Pierwsze twierdzenie o izomorfizmie	Drugie twierdzenie o izomorfizmie	Trzecie twierdzenie o izomorfizmie
	Fraleigh	(bez nazwy)	Drugie twierdzenie o izomorfizmie	Trzecie twierdzenie o izomorfizmie
	Dummit & Foote	Pierwsze twierdzenie o izomorfizmie	Twierdzenie o izomorfizmie drugiego lub diamentowego	Trzecie twierdzenie o izomorfizmie
Brak numeracji	Milne	Twierdzenie o homomorfizmie	Twierdzenie o izomorfizmie	Twierdzenie o korespondencji
	Scott	Twierdzenie o homomorfizmie	Twierdzenie o izomorfizmie	Twierdzenie pierwszego roku

Rzadziej dołącza się twierdzenie D, zwykle znane jako „ twierdzenie kratowe ” lub „twierdzenie o zgodności”, do jednego z twierdzeń o izomorfizmie, ale kiedy tak się dzieje, jest to ostatnie.

Stwierdzenie twierdzeń

Twierdzenie A (grupy)

Niech G i H będą grupami i niech f :  G  →  H będzie homomorfizmem . Następnie:

1. Jądro z F jest normalnie podgrupy z G ,
2. Obraz z F jest podgrupa o H i
3. Obraz f jest izomorficzny z grupą ilorazową G  / ker( f ).

W szczególności, jeśli f jest surjektywne, to H jest izomorficzne z G  / ker( f ).

Twierdzenie B (grupy)

Bądźmy grupą. Niech będzie podgrupą , i niech będzie normalną podgrupą . Następnie następuje następujące wstrzymanie: ${\ Displaystyle G}$${\displaystyle S}$${\ Displaystyle G}$${\ Displaystyle N}$${\ Displaystyle G}$

1. Produkt jest podgrupą ,${\displaystyle SN}$${\ Displaystyle G}$
2. Przecięcia jest normalną podgrupę i${\ Displaystyle S \ czapka N}$${\displaystyle S}$
3. Grupy ilorazowe i są izomorficzne.${\ Displaystyle (SN)/N}$${\ Displaystyle S / (S \ czapka N)}$

Technicznie, nie jest konieczne, aby być normalnym podgrupy, tak długo, jak jest podgrupą normalizer o w . W tym przypadku przecięcie nie jest normalną podgrupą , ale nadal jest normalną podgrupą . ${\ Displaystyle N}$${\displaystyle S}$${\ Displaystyle N}$${\ Displaystyle G}$${\ Displaystyle S \ czapka N}$${\ Displaystyle G}$${\displaystyle S}$

Twierdzenie to jest czasami nazywane „twierdzeniem o izomorfizmie”, „twierdzeniem diamentowym” lub „twierdzeniem równoległym”.

Zastosowanie drugiego twierdzenia o izomorfizmie identyfikuje rzutowe grupy liniowe : na przykład grupa na zespolonej linii rzutowej zaczyna się od ustawienia , grupa odwracalnych macierzy zespolonych 2×2 , podgrupa macierzy wyznacznikowych 1 i podgrupa normalna macierzy skalarnych macierze , mamy , gdzie jest macierz jednostkowa, oraz . Następnie drugie twierdzenie o izomorfizmie stwierdza, że: ${\ Displaystyle G = GL_ {2} (\ mathbb {C} )}$${\displaystyle S=SL_{2}(\mathbb {C})}$${\ Displaystyle N}$${\ Displaystyle \ mathbb {C} ^ {\ razy} \! I = \ lewo \ {\ Bigl (} {\ zacząć {mała matryca} a i 0 \ \ 0 i a \ koniec {mała matryca}} {\ duża}: a \ w \mathbb {C} ^{\times }\right\}}$${\ Displaystyle S \ czapka N = \ {\ pm I \}}$${\ Displaystyle I}$${\displaystyle SN=GL_{2}(\mathbb {C})}$

${\ Displaystyle PGL_ {2} (\ mathbb {C}): = GL_ {2} (\ mathbb {C} )/(\ mathbb {C} ^ {\ razy} \! ja) \ cong SL_ {2} ( \mathbb {C} )/\{\pm I\}=:PSL_{2}(\mathbb {C} )}$

Twierdzenie C (grupy)

Niech będzie grupą i normalną podgrupą . Następnie ${\ Displaystyle G}$${\ Displaystyle N}$${\ Displaystyle G}$

1. Jeśli jest podgrupą takiego, że , to ma podgrupę izomorficzną do .${\ Displaystyle K}$${\ Displaystyle G}$${\ Displaystyle N \ podzbiór K \ podzbiór G}$${\ Displaystyle G/N}$${\ Displaystyle K/N}$
2. Każda podgrupa ma postać pewnego podgrupy w taki sposób, że .${\ Displaystyle G/N}$${\ Displaystyle K/N}$${\ Displaystyle K}$${\ Displaystyle G}$${\ Displaystyle N \ podzbiór K \ podzbiór G}$
3. Jeśli jest normalną podgrupą takiego, że , to ma normalną podgrupę izomorficzną do .${\ Displaystyle K}$${\ Displaystyle G}$${\ Displaystyle N \ podzbiór K \ podzbiór G}$${\ Displaystyle G/N}$${\ Displaystyle K/N}$
4. Każdy normalny podgrupa ma formę jakiegoś normalnego podgrupy w taki sposób, że .${\ Displaystyle G/N}$${\ Displaystyle K/N}$${\ Displaystyle K}$${\ Displaystyle G}$${\ Displaystyle N \ podzbiór K \ podzbiór G}$
5. Jeśli jest normalną podgrupą taką, że , to grupa ilorazowa jest izomorficzna do .${\ Displaystyle K}$${\ Displaystyle G}$${\ Displaystyle N \ podzbiór K \ podzbiór G}$${\ Displaystyle (G/N)/(K/N)}$${\displaystyle G/K}$

Twierdzenie D (grupy)

Twierdzenie korespondencji (znany również jako krata tw) czasem jest zwany trzeci lub czwarty twierdzenie Izomorfizm.

Lemat zassenhausa (znany również jako lematu motylem) czasem jest zwany czwartym twierdzenie Izomorfizm.

Dyskusja

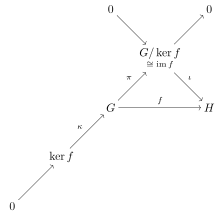
Pierwsze twierdzenie o izomorfizmie można wyrazić w kategorii języka teoretycznego , mówiąc, że kategoria grup jest (normalne epi, mono)-faktoryzowalna; innymi słowy, normalne epimorfizmy i monomorfizmy tworzą system faktoryzacji kategorii. Jest to uchwycone na przemiennym diagramie na marginesie, który pokazuje obiekty i morfizmy, których istnienie można wywnioskować z morfizmu . Diagram pokazuje, że każdy morfizm w kategorii grup ma jądro w sensie teoretycznym kategorii; dowolny morfizm f rozkłada się na , gdzie ι to monomorfizm, a π to epimorfizm (w kategorii konormalnej wszystkie epimorfizmy są normalne). Na diagramie jest to reprezentowane przez obiekt i monomorfizm (jądra są zawsze monomorfizmami), które uzupełniają krótką dokładną sekwencję biegnącą od lewego dolnego rogu do prawego górnego rogu diagramu. Użycie konwencji dokładnej sekwencji oszczędza nam konieczności rysowania zerowych morfizmów z to i . ${\displaystyle f:G\rightarrow H}$${\ Displaystyle \ iota \ circ \ pi}$${\ Displaystyle \ Ker f}$${\displaystyle \kappa:\ker f\rightarrow G}$${\ Displaystyle \ Ker f}$${\ Displaystyle H}$${\displaystyle G/\ker f}$

Jeśli sekwencja jest podzielona prawostronnie (tj. istnieje morfizm σ, który odwzorowuje się na jej wstępny obraz π ), to G jest półbezpośrednim iloczynem normalnej podgrupy i podgrupy . Jeśli jest lewy (tj. istnieją takie, że ), to musi być również prawy i jest bezpośrednim rozkładem iloczynu G . Ogólnie rzecz biorąc, istnienie prawego rozłamu nie implikuje istnienia lewego rozłamu; ale w kategorii abelowej (takiej jak grupy abelowe), podziały lewe i prawe są równoważne przez lemat o rozszczepieniu , a prawy podział jest wystarczający do wytworzenia bezpośredniego rozkładu sumy . W kategorii abelowej wszystkie monomorfizmy są również normalne, a diagram można rozszerzyć o drugą krótką dokładną sekwencję . ${\displaystyle G/\ker f}$${\displaystyle \operatorname {im} \kappa}$${\displaystyle \operatorname {im} \sigma}$${\ Displaystyle \ rho: G \ rightarrow \ Ker f}$${\ Displaystyle \ rho \ circ \ kappa = \ nazwa operatora {id} _ {\ ker f}}$${\ Displaystyle \ operatorname {im} \ kappa \ razy \ operatorname {im} \ sigma}$${\ Displaystyle \ operatorname {im} \ kappa \ oplus \ operatorname {im} \ sigma}$${\displaystyle 0\rightarrow G/\ker f\rightarrow H\rightarrow \operatorname {coker} f\rightarrow 0}$

W drugim twierdzenia izomorfizmu produkt SN jest połączyć z S i N w kratę podgrupy z G , przy czym punkt przecięcia S  ∩  N jest Meet .

Trzecie twierdzenie o izomorfizmie jest uogólnione przez dziewięć lematów na kategorie abelowe i bardziej ogólne odwzorowania między obiektami.

Pierścionki

Twierdzenia twierdzeń o pierścieniach są podobne, przy czym pojęcie normalnej podgrupy zastąpiono pojęciem ideału .

Twierdzenie A (pierścienie)

Niech R i S będą pierścieniami i niech φ :  R  →  S będzie homomorfizmem pierścienia . Następnie:

1. Jądro z cp jest idealny z R ,
2. Obraz z cp jest podpierścień z S i
3. Obraz φ jest izomorficzny z pierścieniem ilorazowym R  / ker( φ ).

W szczególności, jeśli φ jest surjektywne, to S jest izomorficzne z R  / ker( φ ).

Twierdzenie B (pierścienie)

Niech R będzie pierścieniem. Niech S będzie podpierścieniem R , a ja będę ideałem R . Następnie:

1. Suma S  +  I  = { s  +  i  | s  ∈  S ,  i  ∈  I } jest podpierścieniem R ,
2. Przecięcie S  ∩  I jest ideałem S , a
3. Pierścienie ilorazowe ( S  +  I ) /  I i S  / ( S  ∩  I ) są izomorficzne.

Twierdzenie C (pierścienie)

Niech R będzie pierścieniem, a ja ideałem R . Następnie

1. Jeśli jest podpierścieniem takiego, że , to jest podpierścieniem .${\ Displaystyle A}$${\ Displaystyle R}$${\ Displaystyle I \ podsekcji A \ podsekcji R}$${\displaystyle A/I}$${\ Displaystyle R/I}$
2. Każdy z podpierścień ma postać jakiegoś podpierścień w taki sposób, że .${\ Displaystyle R/I}$${\displaystyle A/I}$${\ Displaystyle A}$${\ Displaystyle R}$${\ Displaystyle I \ podsekcji A \ podsekcji R}$
3. Jeśli jest ideałem takiego , to jest ideałem .${\ Displaystyle J}$${\ Displaystyle R}$${\displaystyle I\subseteq J\subseteq R}$${\displaystyle J/I}$${\ Displaystyle R/I}$
4. Każdy ideał jest w postaci jakiegoś ideału w taki sposób, że .${\ Displaystyle R/I}$${\displaystyle J/I}$${\ Displaystyle J}$${\ Displaystyle R}$${\displaystyle I\subseteq J\subseteq R}$
5. Jeśli ideałem jest taki, że , to pierścień ilorazowy jest izomorficzny z .${\ Displaystyle J}$${\ Displaystyle R}$${\displaystyle I\subseteq J\subseteq R}$${\ Displaystyle (R/I)/(J/I)}$${\ Displaystyle R/J}$

Twierdzenie D (pierścienie)

Niech będzie ideałem . Korespondencja jest bijection włączenie zachowując pomiędzy zestawem subrings o które zawierają oraz zestaw subrings o . Ponadto (podpierścień zawierający ) jest ideałem wtedy i tylko wtedy, gdy jest ideałem . ${\ Displaystyle I}$${\ Displaystyle R}$${\displaystyle A\leftrightarrow A/I}$${\ Displaystyle A}$${\ Displaystyle R}$${\ Displaystyle I}$${\ Displaystyle R/I}$${\ Displaystyle A}$${\ Displaystyle I}$${\ Displaystyle R}$${\displaystyle A/I}$${\ Displaystyle R/I}$

Moduły

Stwierdzenia twierdzeń o izomorfizmie dla modułów są szczególnie proste, ponieważ możliwe jest utworzenie modułu ilorazowego z dowolnego podmodułu . Twierdzenia o izomorfizmie dla przestrzeni wektorowych (moduły nad ciałem) i grupy abelowe (moduły nad ) są ich szczególnymi przypadkami. W przypadku skończenie wymiarowych przestrzeni wektorowych wszystkie te twierdzenia wynikają z twierdzenia rang-nullity . ${\ Displaystyle \ mathbb {Z}}$

W dalszej części „moduł” będzie oznaczał „ moduł R ” dla pewnego pierścienia stałego R .

Twierdzenie A (moduły)

Niech M i N będą modułami i niech φ :  M  →  N będzie homomorfizmem modułu . Następnie:

1. Jądro z cp jest modułem z M ,
2. Obraz z cp jest modułem z N i
3. Obraz φ jest izomorficzny z modułem ilorazu M  / ker( φ ).

W szczególności, jeśli φ jest surjektywne, to N jest izomorficzne z M  / ker( φ ).

Twierdzenie B (moduły)

Niech M będzie modułem, a S i T będą podmodułami M . Następnie:

1. Suma S  +  T  = { s  +  t  | s  ∈  S ,  t  ∈  T } jest podmodułem M ,
2. Przecięcie S  ∩  T jest podmodułem M , a
3. Moduły ilorazowe ( S  +  T ) /  T i S  / ( S  ∩  T ) są izomorficzne.

Twierdzenie C (moduły)

Niech M będzie modułem, T submodułem M .

1. Jeśli jest podmodułem takiego, że , to jest podmodułem .${\displaystyle S}$${\ Displaystyle M}$${\displaystyle T\subseteq S\subseteq M}$${\displaystyle S/T}$${\ Displaystyle M/T}$
2. Każdy z modułem jest postaci jakiegoś modułem w taki sposób, że .${\ Displaystyle M/T}$${\displaystyle S/T}$${\displaystyle S}$${\ Displaystyle M}$${\displaystyle T\subseteq S\subseteq M}$
3. Jeśli jest podmodułem takim, że , to moduł ilorazu jest izomorficzny z .${\displaystyle S}$${\ Displaystyle M}$${\displaystyle T\subseteq S\subseteq M}$${\ Displaystyle (M/T)/(S/T)}$${\displaystyle M/S}$

Twierdzenie D (moduły)

Niech będzie modułem, podmodułem . Istnieje bijection między podmodułami tego zawierają i podmodułami . Korespondencja jest udzielana przez dla wszystkich . Ta korespondencja łączy się z procesami przyjmowania sum i przecięć (tzn. jest izomorfizmem sieci między siecią submodułów a siecią submodułów tego, co zawiera ). ${\ Displaystyle M}$${\ Displaystyle N}$${\ Displaystyle M}$${\ Displaystyle M}$${\ Displaystyle N}$${\ Displaystyle M/N}$${\displaystyle A\leftrightarrow A/N}$${\ Displaystyle A \ supseteq N}$${\ Displaystyle M/N}$${\ Displaystyle M}$${\ Displaystyle N}$

Algebra uniwersalna

Aby uogólnić to na uniwersalną algebrę , normalne podgrupy należy zastąpić relacjami przystawalności .

Zbieżność na Algebra jest stosunek równoważności , który tworzy podalgebrą uważane za Algebra z operacjami componentwise. Można przekształcić zbiór klas równoważności w algebrę tego samego typu, definiując działania za pomocą reprezentantów; będzie to dobrze zdefiniowane, ponieważ jest podalgebrą . Wynikowa struktura to algebra ilorazów . ${\ Displaystyle A}$${\ Displaystyle \ Phi \ subseteq A \ razy A}$${\displaystyle A\razy A}$${\ Displaystyle A/\ Phi}$${\ Displaystyle \ Phi}$${\displaystyle A\razy A}$

Twierdzenie A (algebra uniwersalna)

Niech będzie homomorfizmem algebry . Następnie obraz jest podalgebrą relacja podane przez (czyli jądro z ) jest na zbieżność , a algebry i są izomorficzne. (Zauważ, że w przypadku grupy, iff , więc odzyskuje się pojęcie jądra używane w teorii grup w tym przypadku.) ${\displaystyle f:A\rightarrow B}$${\displaystyle f}$${\ Displaystyle B}$${\ Displaystyle \ Phi: f (x) = f (y)}$${\displaystyle f}$${\ Displaystyle A}$${\ Displaystyle \ A/\ Phi \}$${\displaystyle \operatorname {im}f}$${\ Displaystyle f (x) = f (y)}$${\ Displaystyle f \ po lewej (xy ^ {-1} \ po prawej) = 1}$

Twierdzenie B (algebra uniwersalna)

Biorąc pod uwagę algebrę , podalgebrą się i przystawania na , niech będzie śladu w i zbiór klas równoważności, które przecinają . Następnie ${\ Displaystyle A}$${\ Displaystyle B}$${\ Displaystyle A}$${\ Displaystyle \ Phi}$${\ Displaystyle A}$${\ Displaystyle \ Phi _ {B} = \ Phi \ czapka (B \ razy B)}$${\ Displaystyle \ Phi}$${\ Displaystyle B}$${\ Displaystyle [B] ^ {\ Phi} = \ {K \ w A / \ Phi: K \ czapka B \ neq \ pusty zestaw \}}$${\ Displaystyle B}$

1. ${\ Displaystyle \ Phi _ {B}}$jest zbieżnością dnia ,${\ Displaystyle B}$
2. ${\ Displaystyle \ [B] ^ {\ Phi}}$jest podalgebrą , i${\ Displaystyle A/\ Phi}$
3. algebra jest izomorficzna z algebrą .${\ Displaystyle [B] ^ {\ Phi}}$${\ Displaystyle B/\ Phi _ {B}}$

Twierdzenie C (algebra uniwersalna)

Niech będzie algebrą i dwiema relacjami kongruencji na takie, że . Następnie jest kongruencją i jest izomorficzny z . ${\ Displaystyle A}$${\ Displaystyle \ Phi \ psi}$${\ Displaystyle A}$${\ Displaystyle \ psi \ subseteq \ Phi}$${\ Displaystyle \ Phi / \ psi = \ {([a'] _ {\ psi}, [a''] _ {\ psi}): (a', a'') \ w \ Phi \} = [ \ ]_{\Psi }\circ \Phi \circ [\ ]_{\Psi }^{-1}}$${\displaystyle A/\psi}$${\ Displaystyle A/\ Phi}$${\displaystyle (A/\psi)/(\Phi/\psi)}$

Twierdzenie D (algebra uniwersalna)

Niech będzie algebrą i oznacza zbiór wszystkich kongruencji na . Komplet to kompletna krata zamawiana przez włączenie. Jeśli jest kongruencją i oznaczamy zbiorem wszystkich kongruencji, które zawierają (tj. jest filtrem głównym w , a ponadto jest podsiecią), to odwzorowanie jest izomorfizmem sieci. ${\ Displaystyle A}$${\ Displaystyle \ Operatorname {Con} A}$${\ Displaystyle A}$${\ Displaystyle \ Operatorname {Con} A}$${\ Displaystyle \ Phi \ w \ Operatorname {Con} A}$${\ Displaystyle \ lewo [\ Phi, A \ razy A \ prawo] \ podseteq \ Operatorname {Con} A}$${\ Displaystyle \ Phi}$${\ Displaystyle \ lewo [\ Phi, A \ razy A \ po prawej]}$${\ Displaystyle \ Operatorname {Con} A}$${\ Displaystyle \ alfa: \ lewo [\ Phi, A \ razy A \ prawo] \ do \ operatorname {Con} (A/\ Phi), \ psi \ mapsto \ psi / \ Phi}$

Notatka

Bibliografia

• Emmy Noether , Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern , Mathematische Annalen 96 (1927) s. 26-61
• Colin McLarty , „Topologia teorii mnogości Emmy Noether: od Dedekinda do powstania funktorów”. The Architecture of Modern Mathematics: Eseje z historii i filozofii (pod redakcją Jeremy Gray i José Ferreirós), Oxford University Press (2006) s. 211-35.
• Jacobson, Nathan (2009), algebra podstawowa , 1 (2nd ed.), Dover, ISBN 9780486471891
• Paul M. Cohn, Algebra uniwersalna , rozdział II.3 s. 57
• Milne, James S. (2013), Teoria grup , 3.13
• van der Waerden, BI (1994), Algebra , 1 (9 wyd.), Springer-Verlag
• Dummit, David S.; Foote, Richard M. (2004). Algebra abstrakcyjna . Hoboken, NJ: Wiley. Numer ISBN 978-0-471-43334-7.
• Burrisa, Stanleya; Sankappanavar, HP (2012). Kurs algebry uniwersalnej (PDF) . Numer ISBN 978-0-9880552-0-9.
• WR Scott (1964), Teoria grup , Prentice Hall
• John R. Durbin (2009). Nowoczesna Algebra: Wprowadzenie (6 wyd.). Wileya. Numer ISBN 978-0-470-38443-5.
• Anthony W. Knapp (2016), Basic Algebra (Digital Second ed.)
• Pierre Antoine Grillet (2007), Abstrakcyjna Algebra (2 wyd.), Springer
• Joseph J. Rotman (2003), Advanced Modern Algebra (2 wyd.), Prentice Hall, ISBN 0130878685