Mnożenie macierzy - Matrix multiplication

W przypadku mnożenia macierzy liczba kolumn w pierwszej macierzy musi być równa liczbie wierszy w drugiej macierzy. Macierz wynikowa zawiera liczbę wierszy pierwszej i liczbę kolumn drugiej macierzy.

W matematyce , szczególnie w algebrze liniowej , mnożenie macierzy jest operacją binarną, która tworzy macierz z dwóch macierzy. W przypadku mnożenia macierzy liczba kolumn w pierwszej macierzy musi być równa liczbie wierszy w drugiej macierzy. Otrzymana macierz, znana jako iloczyn macierzy , ma liczbę wierszy pierwszej i liczbę kolumn drugiej macierzy. Iloczyn macierzy A i B oznaczamy jako AB .

Mnożenie macierzy został po raz pierwszy opisany przez francuskiego matematyka Jacques Philippe Marie Binet w 1812 roku, do reprezentowania kompozycję z map liniowych , które są reprezentowane przez macierze. Mnożenie macierzy jest zatem podstawowym narzędziem algebry liniowej i jako takie ma liczne zastosowania w wielu dziedzinach matematyki, a także w matematyce stosowanej , statystyce , fizyce , ekonomii i inżynierii . Obliczanie produktów macierzy jest centralną operacją we wszystkich zastosowaniach obliczeniowych algebry liniowej.

Notacja

W tym artykule zostaną zastosowane następujące konwencje notacji: macierze są reprezentowane dużymi literami pogrubionymi, np. A ; wektory pogrubione małymi literami, np. a ; a wpisy wektorów i macierzy są kursywą (ponieważ są to liczby z pola), np. A i a . Notacja indeksowa jest często najjaśniejszym sposobem wyrażania definicji i jest stosowana jako standard w literaturze. , J wejście macierzy A jest wskazany przez ( A ), _ij , A _ij lub w _ij , natomiast podpisem cyfrowym (nie wpisy matrycy) na zbiór macierzy jest indeksowana tylko, na przykład A ₁ , A ₂ , itd.

Definicja

Jeśli A jest macierzą m × n , a B jest macierzą n × p ,

${\ Displaystyle \ mathbf {A} = {\ zacząć {pmatrix} a_ {11} i a_ {12} i \ cdots i a_ {1n} \ \ a_ {21} i a_ {22} \ cdots i a_ {2n} \ \ \ vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix} b_{11}&b_{12}&\cdots &b_{1p}\\b_{21}&b_{22}&\cdots &b_{2p}\\\vdots &\vdots &\ddots &\vdots \\b_{n1 }&b_{n2}&\cdots &b_{np}\\\end{pmatrix}}}$

produkt macierzy C = AB (oznaczonej rozmnażania bez oznaczeń lub punkty) jest określona jako m x p macierz

${\ Displaystyle \ mathbf {C} = {\ zacząć {pmatrix} c_ {11} i c_ {12} i \ cdots i c_ {1 p} \ \ c_ {21} i c_ {22} \ cdots i c_ {2 p} \ \ \ vdots &\vdots &\ddots &\vdots \\c_{m1}&c_{m2}&\cdots &c_{mp}\\\end{pmatrix}}}$

takie, że

${\ Displaystyle c_ {ij} = a_ {i1} b_ {1j} + a_ {i2} b_ {2j} + \ cdots + a_ {w} b_ {nj} = \ suma _ {k = 1} ^ {n} a_{ik}b_{kj},}$

dla i = 1, ..., m oraz j = 1, ..., p .

Oznacza to, że wpis produktu uzyskuje się przez pomnożenie wyraz po wyrazie wpisów i- tego wiersza A i j- tej kolumny B i zsumowanie tych n produktów. Innymi słowy, jest iloczyn skalarny tego ı -tego rzędu A i j tej kolumny B . ${\displaystyle c_{ij}}$${\displaystyle c_{ij}}$

Dlatego AB można również zapisać jako

${\ Displaystyle \ mathbf {C} = {\ zacząć {pmatrix} a_ {11} b_ {11} + \ cdots + a_ {1n} b_ {n1} i a_ {11} b_ {12} + \ cdots + a_ {1n }b_{n2}&\cdots &a_{11}b_{1p}+\cdots +a_{1n}b_{np}\\a_{21}b_{11}+\cdots +a_{2n}b_{n1} &a_{21}b_{12}+\cdots +a_{2n}b_{n2}&\cdots &a_{21}b_{1p}+\cdots +a_{2n}b_{np}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}b_{11}+\cdots +a_{mn}b_{n1}&a_{m1}b_{12}+\cdots +a_{mn}b_{n2}&\ cdots &a_{m1}b_{1p}+\cdots +a_{mn}b_{np}\\\end{pmatrix}}}$

Zatem iloczyn AB jest zdefiniowany wtedy i tylko wtedy, gdy liczba kolumn w A jest równa liczbie wierszy w B , w tym przypadku n .

W większości scenariuszy wpisy są liczbami, ale mogą to być dowolne obiekty matematyczne, dla których zdefiniowano dodawanie i mnożenie, są asocjacyjne i takie, że dodawanie jest przemienne , a mnożenie jest rozdzielne względem dodawania . W szczególności wpisy mogą być same macierzami (patrz macierz blokowa ).

Ilustracja

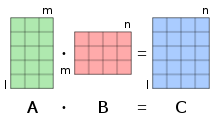
Rysunek po prawej ilustruje schematycznie iloczyn dwóch macierzy A i B , pokazując, jak każde przecięcie w macierzy iloczynu odpowiada rzędowi A i kolumnie B .

${\ Displaystyle {\ przesunięty {4 \ razy 2 {\ tekst {matryca}}} {\ zacząć {bmatrix} {a_ {11}} i {a_ {12}} \ \ \ cdot i \ cdot \ \ {a_ { 31}}&{a_{32}}\\\cdot &\cdot \\\end{bmatrix}}}{\overset {2\times 3{\text{ matrix}}}{\begin{bmatrix}\cdot &{b_{12}}&{b_{13}}\\\cdot &{b_{22}}&{b_{23}}\\\end{bmatrix}}}={\overset {4\times 3 {\text{ matrix}}}{\begin{bmatrix}\cdot &c_{12}&c_{13}\\\cdot &\cdot &\cdot \\\cdot &c_{32}&c_{33}\\\cdot &\cdot &\cdot \\\end{bmatryca}}}}$

Wartości na skrzyżowaniach oznaczonych kółkami to:

${\ Displaystyle {\ zacząć {wyrównany} c_ {12} i = {a_ {11}} {b_ {12}} + {a_ {12}} {b_ {22}} \ \ c_ {33} i = {a_ {31}}{b_{13}}+{a_{32}}{b_{23}}\end{wyrównany}}}$

Podstawowe zastosowania

W przeszłości mnożenie macierzy zostało wprowadzone w celu ułatwienia i wyjaśnienia obliczeń w algebrze liniowej . Ten silny związek między mnożeniem macierzy a algebrą liniową pozostaje fundamentalny w całej matematyce, a także w fizyce , chemii , inżynierii i informatyce .

Mapy liniowe

Jeśli przestrzeń wektorowa ma skończoną bazę , każdy z jej wektorów jest jednoznacznie reprezentowany przez skończony ciąg skalarów, zwany wektorem współrzędnych , którego elementami są współrzędne wektora na podstawie. Te wektory współrzędnych tworzą inną przestrzeń wektorową, która jest izomorficzna z oryginalną przestrzenią wektorową. Wektor współrzędnych jest zwykle zorganizowany jako macierz kolumnowa (zwana również wektorem kolumnowym ), która jest macierzą z tylko jedną kolumną. Tak więc wektor kolumnowy reprezentuje zarówno wektor współrzędnych, jak i wektor oryginalnej przestrzeni wektorowej.

Odwzorowanie liniowe A z przestrzeni wektorowej o wymiarze n na przestrzeń wektorową o wymiarze m odwzorowuje wektor kolumnowy

${\ Displaystyle \ mathbf {x} = {\ zacząć {pmatrix} x_ {1} \ \ x_ {2} \ \ \ vdots \ \ x_ {n} \ koniec {pmatrix}}}$

na wektor kolumnowy

${\ Displaystyle \ mathbf {y} = A (\ mathbf {x}) = {\ zacząć {pmatrix} a_ {11} x_ {1} + \ cdots + a_ {1n} x_ {n} \ \ a_ {21} x_{1}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}\end{pmatrix}}.}$

Mapa liniowa A jest zatem zdefiniowana przez macierz

${\ Displaystyle \ mathbf {A} = {\ zacząć {pmatrix} a_ {11} i a_ {12} i \ cdots i a_ {1n} \ \ a_ {21} i a_ {22} \ cdots i a_ {2n} \ \ \ vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},}$

i odwzorowuje wektor kolumnowy na iloczyn macierzy ${\displaystyle \mathbf {x}}$

${\ Displaystyle \ mathbf {y} = \ mathbf {topór}.}$

Jeśli B jest innym odwzorowaniem liniowym z poprzedzającej przestrzeni wektorowej wymiaru m , do przestrzeni wektorowej wymiaru p , jest reprezentowane przez macierz Proste obliczenie pokazuje , że macierz odwzorowania złożonego jest iloczynem macierzy Ogólny wzór ) , który definiuje skład funkcji jest tu przedstawiony jako szczególny przypadek asocjatywności iloczynu macierzy (patrz § Asocjatywność poniżej): ${\displaystyle p\razy m}$${\ Displaystyle \ mathbf {B} .}$ ${\displaystyle B\circ A}$${\ Displaystyle \ mathbf {BA}.}$${\ Displaystyle (B \ circ A) (\ mathbf {x} ) = B (A (\ mathbf {x} ))}$

${\ Displaystyle (\ mathbf {BA} ) \ mathbf {x} = \ mathbf {B} (\ mathbf {topór} ) = \ mathbf {BAx}.}$

Układ równań liniowych

Ogólna postać układu równań liniowych to

${\ Displaystyle {\ zacząć {macierz} a_ {11} x_ {1} + \ cdots + a_ {1n} x_ {n} = b_ {1} \ \ a_ {21} x_ {1} + \ cdots + a_ { 2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m}\end{macierz}}.}$

Używając tego samego zapisu jak powyżej, taki układ jest równoważny z równaniem jednomacierzowym

${\ Displaystyle \ mathbf {topór} = \ mathbf {b}.}$

Iloczyn skalarny, forma dwuliniowa i iloczyn wewnętrzny

Iloczyn skalarny dwóch wektorów kolumnowych jest iloczynem macierzy

${\ Displaystyle \ mathbf {x} ^ {\ mathsf {T}} \ mathbf {y}}$

gdzie jest wektorem wierszowym uzyskanym przez transpozycję, a uzyskana macierz 1×1 jest identyfikowana za pomocą swojego unikalnego wpisu. ${\ Displaystyle \ mathbf {x} ^ {\ mathsf {T}}}$ ${\displaystyle \mathbf {x}}$

Mówiąc bardziej ogólnie, każda forma dwuliniowa w przestrzeni wektorowej o skończonych wymiarach może być wyrażona jako iloczyn macierzowy

${\ Displaystyle \ mathbf {x} ^ {\ mathsf {T}} \ mathbf {ay}}$

a każdy produkt wewnętrzny może być wyrażony jako

${\ Displaystyle \ mathbf {x} ^ {\ sztylet} \ mathbf {ay}}$

gdzie oznacza sprzężoną transpozycję z (sprzężoną transpozycję lub równoważnie transpozycji koniugatu). ${\ Displaystyle \ mathbf {x} ^ {\ sztylet}}$${\displaystyle \mathbf {x}}$

Właściwości ogólne

Mnożenie macierzy dzieli niektóre właściwości ze zwykłym mnożeniem . Jednak mnożenie macierzy nie jest zdefiniowane, jeśli liczba kolumn pierwszego czynnika różni się od liczby wierszy drugiego czynnika i jest nieprzemienne , nawet jeśli iloczyn pozostaje określony po zmianie kolejności czynników.

Nieprzemienność

Operacja jest przemienna, jeśli przy danych dwóch elementach A i B takich, że iloczyn jest zdefiniowany, to również jest zdefiniowany, a${\ Displaystyle \ mathbf {A} \ mathbf {B}}$${\ Displaystyle \ mathbf {B} \ mathbf {A}}$${\ Displaystyle \ mathbf {A} \ mathbf {B} = \ mathbf {B} \ mathbf {A}.}$

Jeżeli A i B są macierzami o odpowiednich rozmiarach i , to jest definiowane jeżeli , a jest definiowane jeżeli . Dlatego jeśli jeden z produktów jest zdefiniowany, drugi nie jest zdefiniowany w ogóle. Jeśli , dwa produkty są zdefiniowane, ale mają różne rozmiary; dlatego nie mogą być równe. Tylko jeśli , to znaczy, jeśli A i B są macierzami kwadratowymi o tym samym rozmiarze, oba produkty są zdefiniowane i mają ten sam rozmiar. Nawet w tym przypadku generalnie trzeba ${\displaystyle m\razy n}$${\displaystyle p\razy q}$${\ Displaystyle \ mathbf {A} \ mathbf {B}}$${\displaystyle n=p}$${\ Displaystyle \ mathbf {B} \ mathbf {A}}$${\displaystyle m=q}$${\displaystyle m=q\neq n=p}$${\displaystyle m=q=n=p}$

${\ Displaystyle \ mathbf {A} \ mathbf {B} \ neq \ mathbf {B} \ mathbf {A}.}$

Na przykład

${\ Displaystyle {\ zacznij {pmatrix} 0 i 1 \ \ 0 i 0 \ koniec {pmatrix}} {\ zacznij {pmatrix} 0 i 0 \ \ 1 i 0 \ koniec {pmatrix}} = {\ zacznij {pmatrix} 1 i 0 \ \ 0 i 0 \ koniec {pmatrix }},}$

ale

${\ Displaystyle {\ zacznij {pmatrix} 0 i 0 \ \ 1 i 0 \ koniec {pmatrix}} {\ zacznij {pmatrix} 0 i 1 \ \ 0 i 0 \ koniec {pmatrix}} = {\ zacznij {pmatrix} 0 i 0 \ \ 0 i 1 \ koniec {pmatrix }}.}$

Ten przykład można rozszerzyć, aby pokazać, że jeśli A jest macierzą z wpisami w polu F , to dla każdej macierzy B z wpisami w F , wtedy i tylko wtedy , gdy gdzie , a I jest macierzą jednostkową . Jeżeli zamiast pola wpisy mają należeć do ringu , to należy dodać warunek, że c należy do środka ringu. ${\displaystyle n\razy n}$ ${\ Displaystyle \ mathbf {A} \ mathbf {B} = \ mathbf {B} \ mathbf {A}}$${\displaystyle n\razy n}$ ${\ Displaystyle \ mathbf {A} = c \ \ mathbf {ja}}$${\displaystyle c\wf}$${\displaystyle n\razy n}$

Jednym szczególnym przypadkiem, w którym występuje przemienność, jest sytuacja, w której D i E są dwiema (kwadratowymi) macierzami diagonalnymi (tego samego rozmiaru); następnie DE = ED . Ponownie, jeśli macierze znajdują się nad ogólnym pierścieniem, a nie polem, odpowiednie wpisy w każdej z nich muszą również komunikować się ze sobą, aby to się utrzymało.

Dystrybucja

Iloczyn matrycy jest rozdzielczy pod względem dodawania matrycy . Oznacza to, że jeśli A , B , C , D są macierzami o odpowiednich rozmiarach m × n , n × p , n × p i p × q , to należy mieć (lewy rozkład)

${\ Displaystyle \ mathbf {A} (\ mathbf {B} + \ mathbf {C} ) = \ mathbf {AB} + \ mathbf {AC},}$

i (właściwa dystrybucja)

${\ Displaystyle (\ mathbf {B} + \ mathbf {C} ) \ mathbf {D} = \ mathbf {BD} + \ mathbf {CD}}.$

Wynika to z rozdzielności dla współczynników przez

${\ Displaystyle \ suma _ {k} a_ {ik} (b_ {kj} + c_ {kj}) = \ suma _ {k} a_ {ik} b_ {kj} + \ suma _ {k} a_ {ik} c_{kj}}$

${\ Displaystyle \ suma _ {k} (b_ {ik} + c_ {ik}) d_ {kj} = \ suma _ {k} b_ {ik} d_ {kj} + \ suma _ {k} c_ {ik} d_{kj}.}$

Produkt ze skalarem

Jeśli A jest macierzą, a c skalarem, to macierze i są otrzymywane przez pomnożenie wszystkich wpisów A przez c . Jeśli skalary mają własność przemienności , to${\displaystyle c\mathbf {A}}$${\ Displaystyle \ mathbf {A} do}$${\ Displaystyle do \ mathbf {A} = \ mathbf {A} do.}$

Jeśli iloczyn jest zdefiniowany (czyli liczba kolumn A jest równa liczbie rzędów B ), to ${\ Displaystyle \ mathbf {AB}}$

${\ Displaystyle c (\ mathbf {AB} ) = (c \ mathbf {A} ) \ mathbf {B}}$ oraz ${\ Displaystyle (\ mathbf {A} \ mathbf {B}) c = \ mathbf {A} (\ mathbf {B} c).}$

Jeśli skalary mają własność przemienności, to wszystkie cztery macierze są równe. Mówiąc bardziej ogólnie, wszystkie cztery, jeśli są równe C należy do środka z pierścieniem zawierającym dane z macierzy, ponieważ w tym przypadku, c X = X C dla wszystkich macierzy X .

Właściwości te wynikają z dwuliniowości iloczynu skalarów:

${\ Displaystyle c \ lewo (\ suma _ {k} a_ {ik} b_ {kj} \ po prawej) = \ suma _ {k} (ca_ {ik}) b_ {kj}}$

${\ Displaystyle \ lewo (\ suma _ {k} a_ {ik} b_ {kj} \ prawej) c = \ suma _ {k} a_ {ik} (b_ {kj} c).}$

Transponować

Jeśli skalary mają przemienność , to transpozycja iloczynu macierzy jest iloczynem, w odwrotnej kolejności, transpozycji czynników. To jest

${\ Displaystyle (\ mathbf {AB} ) ^ {\ mathsf {T}} = \ mathbf {B} ^ {\ mathsf {T}} \ mathbf {A} ^ {\ mathsf {T}}}$

gdzie ^T oznacza transpozycję, czyli wymianę wierszy i kolumn.

Ta identyczność nie obowiązuje dla nieprzemiennych wpisów, ponieważ kolejność między wpisami A i B jest odwrócona, gdy rozszerza się definicję iloczynu macierzy.

Złożony koniugat

Jeśli A i B mają wpisy złożone , to

${\ Displaystyle (\ mathbf {AB}) ^ {*} = \ mathbf {A} ^ {*} \ mathbf {B} ^ {*}}$

gdzie ^* oznacza złożoną koniugat macierzy.

Wynika to z zastosowania do definicji iloczynu macierzowego faktu, że koniugat sumy jest sumą koniugatów sum, a koniugat produktu jest iloczynem koniugatów tych czynników.

Transpozycja działa na indeksy pozycji, podczas gdy koniugacja działa niezależnie na same pozycje. Wynika z tego, że jeśli A i B mają złożone wpisy, trzeba:

${\ Displaystyle (\ mathbf {AB} ) ^ {\ sztylet} = \ mathbf {B} ^ {\ sztylet} \ mathbf {A} ^ {\ sztylet},}$

gdzie ^† oznacza koniugat transponowany (koniugat transpozycji lub równoważnie transponowany koniugatu).

Łączność

Mając trzy macierze A , B i C , iloczyny ( AB ) C i A ( BC ) są zdefiniowane wtedy i tylko wtedy , gdy liczba kolumn A jest równa liczbie rzędów B , a liczba kolumn B jest równa liczbie wierszy C (w szczególności, jeśli jeden z produktów jest zdefiniowany, to drugi jest również zdefiniowany). W tym przypadku mamy własność asocjacyjną

${\ Displaystyle (\ mathbf {AB} ) \ mathbf {C} = \ mathbf {A} (\ mathbf {BC}).}$

Jeśli chodzi o każdą operację asocjacyjną, pozwala to na pominięcie nawiasów i zapisanie powyższych produktów jako ${\ Displaystyle \ mathbf {ABC}.}$

Rozciąga się to naturalnie na iloczyn dowolnej liczby matryc, pod warunkiem, że wymiary się zgadzają. To znaczy, jeśli A ₁ , A ₂ , ..., A _n są macierzami takimi, że liczba kolumn A _i jest równa liczbie wierszy A _{i + 1} dla i = 1, ..., n – 1 , następnie produkt

${\ Displaystyle \ prod _ {i = 1} ^ {n} \ mathbf {A} _ {i} = \ mathbf {A} _ {1} \ mathbf {A} _ {2} \ cdots \ mathbf {A} _{n}}$

jest zdefiniowana i nie zależy od kolejności mnożenia , jeśli kolejność macierzy jest stała.

Te właściwości można udowodnić za pomocą prostych, ale skomplikowanych operacji sumowania . Wynik ten wynika również z faktu, że macierze reprezentują odwzorowania liniowe . Dlatego też asocjacyjna własność macierzy jest po prostu szczególnym przypadkiem asocjacyjnej własności składania funkcji .

Złożoność nie jest asocjacyjna

Chociaż wynik sekwencji iloczynów macierzy nie zależy od kolejności operacji (pod warunkiem, że kolejność macierzy nie zostanie zmieniona), złożoność obliczeniowa może dramatycznie zależeć od tej kolejności.

Na przykład, jeśli A , B i C są macierzami o odpowiednich rozmiarach 10×30, 30×5, 5×60 , obliczenie ( AB ) C wymaga 10×30×5 + 10×5×60 = 4500 mnożenia, natomiast obliczenie A ( BC ) wymaga 30×5×60 + 10×30×60 = 27 000 mnożenia.

Algorytmy zostały zaprojektowane w celu wyboru najlepszej kolejności produktów, patrz Mnożenie łańcucha macierzy . Gdy liczba n macierzy wzrasta, wykazano, że wybór najlepszego rzędu ma złożoność${\ Displaystyle O (n \ log n).}$

Zastosowanie do podobieństwa

Każda macierz odwracalna definiuje transformację podobieństwa (na macierzach kwadratowych o tym samym rozmiarze co ) ${\ Displaystyle \ mathbf {P} }$${\ Displaystyle \ mathbf {P} }$

${\ Displaystyle S_ {\ mathbf {P}} (\ mathbf {A} ) = \ mathbf {P} ^ {-1} \ mathbf {A} \ mathbf {P}.}$

Transformacje podobieństwa mapują produkt na produkty, czyli

${\ Displaystyle S_ {\ mathbf {P} } (\ mathbf {AB} ) = S_ {\ mathbf {P}} (\ mathbf {A}) S_ {\ mathbf {P}} (\ mathbf {B}). }$

W rzeczywistości trzeba

${\ Displaystyle \ mathbf {P} ^ {-1} (\ mathbf {AB}) \ mathbf {P} = \ mathbf {P} ^ {-1} \ mathbf {A} (\ mathbf {P} \ mathbf { P} ^{-1})\mathbf {B} \mathbf {P} =(\mathbf {P} ^{-1}\mathbf {A} \mathbf {P} )(\mathbf {P} ^{- 1}\mathbf {B} \mathbf {P} ).}$

Macierze kwadratowe

Oznaczmy zbiór n × n macierzy kwadratowych z wpisami w pierścieniu R , który w praktyce jest często ciałem . ${\ Displaystyle {\ Mathcal {M}} _ {n} (R)}$

W , iloczyn jest definiowany dla każdej pary macierzy. Tworzy to pierścień , który ma macierz jednostkową I jako element tożsamościowy (macierz, której wpisy przekątne są równe 1, a wszystkie inne wpisy są równe 0). Ten pierścień jest również asocjacyjną R- algebrą . ${\ Displaystyle {\ Mathcal {M}} _ {n} (R)}$${\ Displaystyle {\ Mathcal {M}} _ {n} (R)}$

Jeśli n > 1 , wiele macierzy nie posiada odwrotności multiplikatywnej . Na przykład macierz, w której wszystkie wpisy wiersza (lub kolumny) mają wartość 0, nie ma odwrotności. Jeśli istnieje, odwrotność macierzy A oznaczamy A ⁻¹ , a zatem weryfikuje

${\ Displaystyle \ mathbf {A} \ mathbf {A} ^ {-1} = \ mathbf {A} ^ {-1} \ mathbf {A} = \ mathbf {I}.}$

Macierz, która ma odwrotność, jest macierzą odwracalną . W przeciwnym razie jest to pojedyncza macierz .

Iloczyn macierzy jest odwracalny wtedy i tylko wtedy, gdy każdy czynnik jest odwracalny. W tym przypadku trzeba

${\ Displaystyle (\ mathbf {A} \ mathbf {B} ) ^ {-1} = \ mathbf {B} ^ {-1} \ mathbf {A} ^ {-1}.}$

Gdy R jest przemienne , aw szczególności, gdy jest polem, wyznacznikiem iloczynu jest iloczyn wyznaczników. Ponieważ wyznacznikami są skalary, a skalary przechodzą, mamy zatem:

${\displaystyle \det(\mathbf {AB})=\det(\mathbf {BA})=\det(\mathbf {A})\det(\mathbf {B}).}$

Inne niezmienniki macierzy nie zachowują się tak dobrze z produktami. Niemniej jednak, jeśli R jest przemienne, AB i BA mają ten sam ślad , ten sam wielomian charakterystyczny i te same wartości własne z tymi samymi krotnościami. Jednak wektory własne są ogólnie różne, jeśli AB ≠ BA .

Potęgi macierzy

Macierz kwadratową można podnieść do dowolnej nieujemnej potęgi całkowitej, mnożąc ją wielokrotnie przez siebie w taki sam sposób, jak w przypadku zwykłych liczb. To jest,

${\ Displaystyle \ mathbf {A} ^ {0} = \ mathbf {ja}}$

${\ Displaystyle \ mathbf {A} ^ {1} = \ mathbf {A}}$

${\ Displaystyle \ mathbf {A} ^ {k} = \ Underbrace {\ mathbf {A} \ mathbf {A} \ cdots \ mathbf {A}} _ {k {\ tekst {razy}}}.}$

Obliczenie k- tej potęgi macierzy wymaga k – 1- krotności czasu pojedynczego mnożenia macierzy, jeśli odbywa się to algorytmem trywialnym (mnożenie wielokrotne). Jak to może być bardzo czasochłonne, jeden generalnie preferuje stosując algorytm szybkiego potęgowania , która wymaga mniej niż 2 log ₂ k mnożenie macierzy, a więc jest znacznie bardziej wydajne.

Łatwym przypadkiem potęgowania jest macierz diagonalna . Ponieważ iloczyn macierzy diagonalnych sprowadza się do prostego pomnożenia przez siebie odpowiednich elementów diagonalnych, k- tą potęgę macierzy diagonalnej uzyskuje się przez podniesienie wpisów do potęgi k :

${\ Displaystyle {\ zacząć {bmatrix} a_ {11} i 0 & \ cdots & 0 \ \ 0 & a_ {22} & \ cdots & 0 \ \ \ vdots & \ vdots & \ ddots & \ vdots \ \ 0 i 0 & \ cdots & a_ {nn} \ end{bmatrix}}^{k}={\begin{bmatrix}a_{11}^{k}&0&\cdots &0\\0&a_{22}^{k}&\cdots &0\\\vdots &\vdots & \ddots &\vdots \\0&0&\cdots &a_{nn}^{k}\end{bmatrix}}.}$

Algebra abstrakcyjna

Definicja iloczynu macierzowego wymaga, aby wpisy należały do ​​semiringu i nie wymaga, aby mnożenie elementów semiringu było przemienne . W wielu zastosowaniach elementy macierzy należą do dziedziny, chociaż tropikalny półpierścień jest również powszechnym wyborem w przypadku problemów z najkrótszą ścieżką grafu . Nawet w przypadku macierzy nad polami iloczyn w ogólności nie jest przemienny, chociaż jest asocjacyjny i dystrybucyjny względem dodawania macierzy . W macierzy tożsamości (które są macierze kwadratowe , których prace są równe zero na zewnątrz głównego przekątnej i 1 na głównej przekątna) są elementy identyfikacyjne produktu matrycy. Wynika z tego, że macierze n × n nad pierścieniem tworzą pierścień, który jest nieprzemienny, chyba że n = 1, a pierścień uziemienia jest przemienny.

Macierz kwadratowa może mieć odwrotność multiplikatywną , zwaną macierzą odwrotną . W powszechnym przypadku, gdy wpisy należą do pierścienia przemiennego r , macierz ma odwrotność wtedy i tylko wtedy, gdy jej wyznacznik ma odwrotność multiplikatywną w r . Wyznacznik iloczynu macierzy kwadratowych jest iloczynem wyznaczników czynników. N x n macierzy, które mają odwrotny, tworzą grupę względem mnożenia macierzy tej podgrupy , które są nazywane grupami matrycy . Wiele grup klasycznych (w tym wszystkie grupy skończone ) jest izomorficznych z grupami macierzowymi; to jest punkt wyjścia teorii reprezentacji grupowych .

Złożoność obliczeniowa

Poprawa estymacji wykładnika ω w czasie dla złożoności obliczeniowej mnożenia macierzy .${\ Displaystyle O (n ^ {\ omega})}$

Mnożenie macierzy algorytm , który wynika z definicji wymaga w najgorszym przypadku , mnożenia i dodatki skalarów obliczyć iloczyn dwóch kwadratowych n x n macierzy. Jego złożoność obliczeniowa jest zatem , w modelu obliczeń, dla którego operacje skalarne trwają stały czas (w praktyce dotyczy to liczb zmiennoprzecinkowych , ale nie liczb całkowitych). ${\ Displaystyle n ^ {3}}$${\ Displaystyle (n-1) n ^ {2}}$${\ Displaystyle O (n ^ {3})}$

Co zaskakujące, ta złożoność nie jest optymalna, jak wykazał w 1969 roku Volker Strassen , który dostarczył algorytm, obecnie nazywany algorytmem Strassena , ze złożonością algorytmu Strassena, który można zrównoleglać w celu dalszej poprawy wydajności. Od grudnia 2020 r. najlepszy algorytm mnożenia macierzy został opracowany przez Josha Almana i Virginię Vassilevska Williams i ma złożoność O ( n ^2.3728596 ) . Nie wiadomo, czy mnożenie macierzy można wykonać w czasie O ( n ^{2 + o(1)} ) . Byłoby to optymalne, ponieważ trzeba odczytać elementy macierzy, aby pomnożyć ją przez inną macierz. ${\ Displaystyle O (n ^ {\ log _ {2} 7}) \ w przybliżeniu O (n ^ {2.8074}).}$${\displaystyle n^{2}}$

Ponieważ mnożenie macierzy stanowi podstawę wielu algorytmów, a wiele operacji na macierzach ma nawet taką samą złożoność, jak mnożenie macierzy (aż do stałej mnożenia), złożoność obliczeniowa mnożenia macierzy pojawia się w numerycznej algebrze liniowej i informatyce teoretycznej .

Uogólnienia

Inne rodzaje produktów matryc to:

• Mnożenie macierzy bloków
• Produkt krakowski , zdefiniowany jako A ∧ B = B ^T A
• Iloczyn skalarny Frobeniusa , iloczyn skalarny macierzy traktowanych jako wektory lub równoważnie suma pozycji iloczynu Hadamarda
• Iloczyn Hadamarda dwóch macierzy o tej samej wielkości, co skutkuje macierzą o tej samej wielkości, która jest produktem wejścia po wejściu
• Iloczyn Kroneckera lub iloczyn tensorowy , uogólnienie na dowolny rozmiar poprzedniego
• Produkt Khatri-Rao i produkt do dzielenia twarzy
• Produkt zewnętrzny , zwany także produkt dwójkowym lub tensorowy produkt dwóch kolumn macierzy, co jest${\ Displaystyle \ mathbf {a} \ mathbf {b} ^ {\ mathsf {T}}}$
• Mnożenie przez skalar

Zobacz też

• Rachunek macierzowy , do interakcji mnożenia macierzy z operacjami z rachunku różniczkowego

Uwagi

Bibliografia