Kula Riemanna - Riemann sphere

Sferę Riemanna można zobrazować jako płaszczyznę liczby zespolonej owiniętą wokół kuli (za pomocą jakiejś formy rzutowania stereograficznego – szczegóły poniżej).

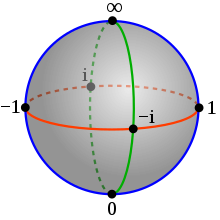
W matematyce , sfera Riemanna , nazwany Bernhard Riemann , jest modelem z rozszerzonym płaszczyźnie zespolonej The kompleks samolot plus punkt w nieskończoności . Ta rozszerzona płaszczyzna reprezentuje rozszerzone liczby zespolone , czyli liczby zespolone plus wartość ∞ dla nieskończoności . W modelu Riemanna punkt „∞” jest blisko bardzo dużych liczb, tak jak punkt „0” jest blisko bardzo małych liczb.

Rozszerzone liczby zespolone są przydatne w analizie zespolonej, ponieważ pozwalają w pewnych okolicznościach na dzielenie przez zero w sposób, który sprawia, że ​​wyrażenia takie jak dobrze zachowują się . Na przykład każda funkcja wymierna na płaszczyźnie zespolonej może zostać rozszerzona do funkcji holomorficznej na sferze Riemanna, z biegunami funkcji wymiernej odwzorowanymi w nieskończoność. Bardziej ogólnie, każda funkcja meromorficzna może być traktowana jako funkcja holomorficzna, której przeciwdziedziną jest sfera Riemanna. ${\displaystyle {\tfrac {1}{0}}=\infty}$

W geometrii sfera Riemanna jest prototypowym przykładem powierzchni Riemanna i jest jedną z najprostszych złożonych rozmaitości . W geometrii rzutowej sferę można traktować jako złożoną linię rzutową P ¹ ( C ) , przestrzeń rzutową wszystkich linii złożonych w C ² . Jak w przypadku każdej zwartej powierzchni Riemanna, sferę można również postrzegać jako rzutową krzywą algebraiczną , co czyni ją podstawowym przykładem w geometrii algebraicznej . Znajduje on również zastosowanie w innych dziedzinach, które zależą od geometrii i analizy, takimi jak Bloch zakresie od mechaniki kwantowej i w innych gałęziach fizyki .

Rozszerzona płaszczyzna złożona jest również nazywana zamkniętą płaszczyzną złożoną .

Rozszerzone liczby zespolone

Te wydłużone liczb zespolonych składa się z liczb zespolonych C razem z ∞. Zbiór rozszerzonych liczb zespolonych może być zapisany jako C ∪ {∞} i jest często oznaczany przez dodanie dekoracji do litery C , na przykład

${\displaystyle {\kapelusz {\mathbb {C}}},\quad {\overline {\mathbb {C}}},\quad {\tekst {lub}}\quad \mathbb {C} _{\infty} .}$

Geometrycznie zbiór rozszerzonych liczb zespolonych jest określany jako sfera Riemanna (lub rozszerzona płaszczyzna zespolona ).

Działania arytmetyczne

Dodawanie liczb zespolonych można rozszerzyć definiując, dla z ∈ C ,

${\displaystyle z+\infty =\infty}$

dla dowolnej liczby zespolonej z , a mnożenie można zdefiniować przez

${\displaystyle z\razy \infty =\infty}$

dla wszystkich niezerowych liczb zespolonych z , gdzie ∞ × ∞ = ∞ . Zauważ, że ∞ − ∞ i 0 × ∞ pozostają niezdefiniowane . W przeciwieństwie do liczb zespolonych, rozszerzone liczby zespolone nie tworzą pola , ponieważ ∞ nie ma odwrotności addytywnej ani multiplikatywnej . Niemniej jednak zwyczajowo definiuje się dzielenie na C ∪ {∞ } przez

${\displaystyle {\frac {z}{0}}=\infty \quad {\tekst {i}}\quad {\frac {z}{\infty}}=0}$

dla wszystkich niezerowych liczb zespolonych z z ∞/0= ∞ i0/∞= 0 . Iloraz0/0 oraz ∞/∞ pozostają niezdefiniowane.

Funkcje wymierne

Dowolna funkcja wymierna f ( z ) =g ( z )/h ( z )(innymi słowy, f ( z ) jest stosunkiem funkcji wielomianowych g ( z ) i h ( z ) z z ze złożonymi współczynnikami, tak że g ( z ) i h ( z ) nie mają wspólnego współczynnika) można rozszerzyć do funkcją ciągłą na Sfera Riemanna. W szczególności, jeśli z ₀ jest liczbą zespoloną taką, że mianownik h ( z ₀ ) wynosi zero, ale licznik g ( z ₀ ) jest niezerowy, to f ( z ₀ ) można zdefiniować jako ∞. Co więcej, F (∞) może być zdefiniowana jako ograniczenie od f ( oo ) jako Z → ∞ , który może być określony albo nieskończoności.

Zbiór złożonych funkcji wymiernych — których matematycznym symbolem jest C ( z ) — tworzy wszystkie możliwe funkcje holomorficzne ze sfery Riemanna, gdy jest postrzegana jako powierzchnia Riemanna , z wyjątkiem stałej funkcji przyjmującej wszędzie wartość ∞. Funkcje C ( z ) tworzą ciało algebraiczne, zwane ciałem funkcji wymiernych na sferze .

Na przykład, biorąc pod uwagę funkcję

${\ Displaystyle f (z) = {\ Frac {6z ^ {2}+1} {2z ^ {2}-50}}}$

możemy zdefiniować f (±5) = ∞ , ponieważ mianownik wynosi zero przy z = ±5 i f (∞) = 3 ponieważ f ( z ) → 3 jako z → ∞ . Używając tych definicji, f staje się funkcją ciągłą od sfery Riemanna do niej samej.

Jako złożona rozmaitość

Jako jednowymiarowa rozmaitość zespolona, ​​sferę Riemanna można opisać za pomocą dwóch wykresów, przy czym oba mają dziedzinę równą płaszczyźnie liczby zespolonej C . Niech ζ będzie liczbą zespoloną w jednej kopii C , i niech ξ będzie liczbą zespoloną w innej kopii C . Zidentyfikuj każdą niezerową liczbę zespoloną ζ pierwszego C z niezerową liczbą zespoloną1/ξdrugiego C . Następnie mapa

${\ Displaystyle f (z) = {\ Frac {1} {z}}}$

nazywa się mapą przejścia między dwiema kopiami C — tak zwanymi wykresami — sklejając je ze sobą. Ponieważ mapy przejść są holomorficzne , definiują złożoną rozmaitość, zwaną sferą Riemanna . Jako złożona rozmaitość o 1 złożonym wymiarze (tj. 2 rzeczywistych wymiarach), jest ona również nazywana powierzchnią Riemanna .

Intuicyjnie mapy przejść wskazują, jak skleić ze sobą dwie płaszczyzny, aby utworzyć sferę Riemanna. Płaszczyzny są sklejone „od wewnątrz”, tak że nakładają się prawie wszędzie, przy czym każda płaszczyzna ma tylko jeden punkt (jego początek) brakuje w drugiej płaszczyźnie. Innymi słowy, (prawie) każdy punkt w sferze Riemanna ma zarówno wartość ζ, jak i wartość ξ , a te dwie wartości są powiązane przez ζ =1/ξ. Punkt, w którym ξ = 0 powinien mieć wtedy wartość ζ "1/0"; w tym sensie początek wykresu ξ odgrywa rolę "∞" na wykresie ζ . Symetrycznie początek wykresu ζ odgrywa rolę ∞ na wykresie ξ .

Topologicznie powstała przestrzeń jest jednopunktowym zagęszczeniem płaszczyzny w kulę. Sfera Riemanna nie jest jednak tylko sferą topologiczną. Jest to sfera o dobrze zdefiniowanej złożonej strukturze , tak że wokół każdego punktu na sferze znajduje się sąsiedztwo, które można biholomorficznie utożsamić z C .

Z drugiej strony twierdzenie o uniformizacji , centralny wynik w klasyfikacji powierzchni Riemanna, stwierdza, że ​​każda prosto połączona powierzchnia Riemanna jest biholomorficzna w stosunku do płaszczyzny zespolonej, płaszczyzny hiperbolicznej lub sfery Riemanna. Spośród nich sfera Riemanna jest jedyną, która jest powierzchnią zamkniętą ( powierzchnia zwarta bez granic ). Stąd dwuwymiarowa sfera dopuszcza unikalną złożoną strukturę, zamieniając ją w jednowymiarową złożoną rozmaitość.

Jako złożona linia rzutowa

Sferę Riemanna można również określić jako złożoną linię rzutową . Punkty złożonej prostej rzutowej są klasami równoważności wyznaczonymi przez następującą zależność na punktach z C ² \ {(0,0)}:

Jeśli dla niektórych λ ≠ 0, w = λ u i z = λ v , to${\displaystyle (w,z)\grubość (u,v).}$

W tym przypadku klasa równoważności jest zapisana [ w, z ] za pomocą współrzędnych rzutowych . Mając dowolny punkt [ w, z ] w zespolonej prostej rzutowej, jeden z w i z musi być niezerowy, powiedzmy w ≠ 0. Wtedy przez relację równoważności,

${\ Displaystyle [W, Z] \ Grubości \ lewo [1, {\ Tfrac {Z} {W}} \ Prawo]}$ który znajduje się na wykresie dla rozmaitości sfer Riemanna.

Ta obróbka sfery Riemanna najłatwiej łączy się z geometrią rzutową. Na przykład każda linia (lub gładka stożkowa) w złożonej płaszczyźnie rzutowej jest biholomorficzna w stosunku do złożonej linii rzutowej. Jest to również wygodne do badania automorfizmów sfery , w dalszej części tego artykułu.

Jako kula

Rzut stereograficzny liczby zespolonej A na punkt α sfery Riemanna

Sferę Riemanna można wizualizować jako sferę jednostkową x ²  +  y ²  +  z ²  = 1 w trójwymiarowej przestrzeni rzeczywistej R ³ . W tym celu rozważmy rzut stereograficzny ze sfery jednostkowej minus punkt (0, 0, 1) na płaszczyznę z  = 0, którą utożsamiamy z płaszczyzną zespoloną przez ζ = x + iy . W kartezjańskim układzie współrzędnych ( x , y , z ) i współrzędnych sferycznych ( θ , cp ) w dziedzinie (z θ zenitu i cp do azymutu ), przy czym występ jest

${\ Displaystyle \ zeta = {\ Frac {x + iy} {1-z}} = \ łóżeczko \ lewo ({\ Frac {1} {2}} \ theta \ prawej) \; e ^ {i \ phi} .}$

Podobnie zapisuje się rzut stereograficzny od (0, 0, −1) na płaszczyznę z = 0 , identyfikowaną z inną kopią płaszczyzny zespolonej przez ξ = x − iy ,

${\ Displaystyle \ xi = {\ Frac {x-iy} {1 + z}} = \ tan \ lewo ({\ Frac {1} {2}} \ theta \ prawej) \; e ^ {-i \ phi }.}$

Aby pokryć sferę jednostkową potrzebne są dwa rzuty stereograficzne: pierwszy obejmie całą sferę z wyjątkiem punktu (0, 0, 1), a drugi poza punktem  (0, 0, −1) . Stąd potrzebne są dwie złożone płaszczyzny, po jednej dla każdego rzutu, które można intuicyjnie postrzegać jako sklejone plecami do siebie przy  z = 0 . Zauważ, że dwie płaszczyzny zespolone są różnie identyfikowane z płaszczyzną z = 0 . Orientacji -reversal jest niezbędny do utrzymania spójnego orientację w dziedzinie, w szczególności złożone sprzężenie powoduje przejście odwzorowuje się holomorficzny.

Przejście pomiędzy odwzorowuje ζ -coordinates i Ę -coordinates uzyskuje się poprzez komponowanie jeden występ z odwrotności drugiej. Okazuje się, że to ζ =1/ξoraz ξ =1/ζ, jak opisano powyżej. Sfera jednostkowa jest zatem dyfeomorficzna ze sferą Riemanna.

W ramach tego dyfeomorfizmu identyfikuje się okrąg jednostkowy na wykresie ζ , okrąg jednostkowy na wykresie ξ i równik sfery jednostkowej. Dysk jednostkowy | ç | < 1 utożsamiany jest z półkulą południową z < 0 , natomiast dysk jednostkowy | Ę | < 1 jest utożsamiany z półkulą północną  z > 0 .

Metryczny

Powierzchnia Riemanna nie jest wyposażona w żadną konkretną metrykę Riemanna . Struktura konforemna powierzchni Riemanna determinuje jednak klasę metryk: wszystkie te, których podrzędna struktura konforemna jest dana. Bardziej szczegółowo: Złożona struktura powierzchni Riemanna w unikalny sposób określa metrykę aż do konformalnej równoważności . (Dwie metryki są uważane za konformalnie równoważne, jeśli różnią się przez pomnożenie przez dodatnią gładką funkcję ). Odwrotnie, każda metryka na zorientowanej powierzchni jednoznacznie określa złożoną strukturę, która zależy od metryki tylko do równoważności konforemnej. Złożone struktury na zorientowanej powierzchni odpowiadają zatem jeden do jednego z konforemnymi klasami metryk na tej powierzchni.

W obrębie danej klasy konforemnej można użyć symetrii konforemnej, aby znaleźć reprezentatywną metrykę o dogodnych właściwościach. W szczególności zawsze istnieje pełna metryka o stałej krzywiźnie w dowolnej danej klasie konforemnej.

W przypadku sfery Riemanna twierdzenie Gaussa-Bonneta oznacza, że ​​metryka o stałej krzywiźnie musi mieć dodatnią krzywiznę K . Wynika z tego, że metryka musi być izometryczna do sfery o promieniu1/√ Kw R ³ poprzez projekcję stereograficzną. Na wykresie ζ na sferze Riemanna metryka z K = 1 jest dana wzorem

${\ Displaystyle ds ^ {2} = \ lewo ({\ Frac {2} {1 + | \ zeta | ^ {2}}} \ prawej) ^ {2} \ | d \ zeta | ^ {2} = {\frac {4}{\left(1+\zeta {\bar {\zeta }}\right)^{2}}}\,d\zeta \,d{\bar {\zeta }}.}$

W rzeczywistych współrzędnych ζ = u + iv , wzór to

${\ Displaystyle ds ^ {2} = {\ Frac {4} {\ po lewej (1 + u ^ {2} + v ^ {2} \ po prawej) ^ {2}}} \ po lewej (du ^ {2} + dv^{2}\prawo).}$

Aż do stałego współczynnika, metryka ta zgadza się ze standardową metryką Fubini-Study na złożonej przestrzeni rzutowej (której przykładem jest sfera Riemanna).

Do skalowania jest to jedyna metryka w sferze, której grupa izometrii zachowujących orientację jest 3-wymiarowa (i żadna nie jest więcej niż 3-wymiarowa); grupa ta nazywa się SO(3) . W tym sensie jest to zdecydowanie najbardziej symetryczna metryka w sferze. (Grupa wszystkich izometrii, znana jako O(3) , jest również trójwymiarowa, ale w przeciwieństwie do SO(3) nie jest przestrzenią spójną).

I odwrotnie, niech S oznacza sferę (jako abstrakcyjną gładką lub topologiczną rozmaitość ). Zgodnie z twierdzeniem o uniformizacji istnieje unikalna struktura złożona na S , aż do równoważności konforemnej. Wynika z tego, że każda metryka na S jest równoważna metryce okrągłej . Wszystkie takie metryki określają tę samą geometrię konformalną. Okrągła metryka nie jest zatem nierozerwalnie związana ze sferą Riemanna, ponieważ „okrągłość” nie jest niezmiennikiem geometrii konforemnej. Sfera Riemanna jest tylko rozmaitością konforemną , a nie rozmaitością riemannowską . Jeśli jednak trzeba wykonać geometrię Riemanna na sferze Riemanna, naturalnym wyborem jest metryka okrągła (przy dowolnym stałym promieniu, chociaż promień = 1 jest najprostszym i najczęstszym wyborem). To dlatego, że tylko okrągła metryka na sferze Riemanna ma swoją grupę izometryczną jako grupę trójwymiarową. (Mianowicie grupa znana jako SO(3) , grupa ciągła ("Kłamstwo"), która jest topologicznie trójwymiarową przestrzenią rzutową P ³ .)

Automorfizmy

Möbiusa transformacja działając na kuli, a na płaszczyźnie przez stereograficznego

Badanie dowolnego obiektu matematycznego jest wspomagane przez zrozumienie jego grupy automorfizmów, czyli map od obiektu do samego siebie, które zachowują podstawową strukturę obiektu. W przypadku sfery Riemanna automorfizm jest odwracalną mapą konformalną (tj. mapą biholomorficzną) ze sfery Riemanna na samą siebie. Okazuje się, że jedynymi takimi mapami są transformacje Möbiusa . To są funkcje formy

${\ Displaystyle f (\ zeta ) = {\ Frac {a \ zeta + b} {c \ zeta + d}}}$

gdzie a , b , c i d są liczbami zespolonymi takimi, że ad − bc ≠ 0 . Przykłady transformacji Möbiusa obejmują dylatacje , rotacje , translacje i złożoną inwersję . W rzeczywistości każda transformacja Möbiusa może być napisana jako ich kompozycja.

Transformacje Möbiusa to homografie na złożonej linii rzutowej. We współrzędnych rzutowych można zapisać transformację f

${\ Displaystyle [\ zeta, \ 1] {\ zacząć {pmatrix} a & c \ \ b i d \ koniec {pmatrix}} \ = \ [a \ zeta + b, \ c \ zeta + d] \ = \ \ lewo [{ \tfrac {a\zeta +b}{c\zeta +d}},\ 1\right]\ =\ [f(\zeta ),\ 1].}$

Zatem transformacje Möbiusa można opisać jako macierze złożone 2 × 2 z niezerowym wyznacznikiem . Ponieważ działają na współrzędnych rzutowych, dwie macierze dają tę samą transformację Möbiusa wtedy i tylko wtedy, gdy różnią się niezerowym czynnikiem. Grupa przemian MöBIUS jest rzutowa liniową grupę PGL (2 C ) .

Jeśli nada się sferze Riemanna metrykę Fubini-Study , to nie wszystkie transformacje Möbiusa są izometriami; na przykład dylatacje i tłumaczenia nie są. Izometrie tworzą odpowiednią podgrupę PGL(2, C ) , a mianowicie PSU(2). Ta podgrupa jest izomorficzna z grupą rotacyjną SO(3) , która jest grupą symetrii sfery jednostkowej w R ³ (która, gdy jest ograniczona do sfery, staje się izometriami sfery).

Aplikacje

W analizie złożonej funkcja meromorficzna na płaszczyźnie zespolonej (lub na dowolnej powierzchni Riemanna) jest stosunkiem F/gdwóch funkcji holomorficznych f i g . Jako odwzorowanie liczb zespolonych jest niezdefiniowane, gdzie g wynosi zero. Jednak indukuje holomorficzną mapę ( f , g ) do złożonej linii rzutowej, która jest dobrze zdefiniowana, nawet gdy g = 0 . Konstrukcja ta jest pomocna w badaniu funkcji holomorficznych i meromorficznych. Na przykład na zwartej powierzchni Riemanna nie ma niestałych holomorficznych map na liczby zespolone, ale holomorficzne mapy na zespoloną linię rzutową są obfite.

Sfera Riemanna ma wiele zastosowań w fizyce. W mechanice kwantowej, punkty kompleksowej linii projekcyjnej są walory przyrodnicze dla fotonów polaryzacyjnych Zjednoczonych wirowania stany masywnych cząstek o spinie1/2, i ogólnie cząstki dwustanowe (patrz także bit kwantowy i sfera Blocha ). Sfera Riemanna została zaproponowana jako model relatywistyczny dla sfery niebieskiej . W teorii strun , że worldsheets ciągów są powierzchnie Riemanna, a sfera Riemanna, będąc najprostszym powierzchnia Riemanna, odgrywa znaczącą rolę. Jest to również ważne w teorii twistora .

Zobacz też

• Geometria konforemna
• Stosunek krzyżowy
• Dessin d'enfant
• Skierowana nieskończoność
• Pakiet Hopf
• Samolot Möbiusa
• Projekcyjnie rozszerzona linia rzeczywista

Bibliografia

• Brown, James i Churchill, Ruel (1989). Złożone zmienne i aplikacje . Nowy Jork: McGraw-Hill. Numer ISBN 0-07-010905-2.
• Griffiths, Phillip i Harris, Joseph (1978). Zasady geometrii algebraicznej . John Wiley & Synowie. Numer ISBN 0-471-32792-1.
• Penrose, Roger (2005). Droga do rzeczywistości . Nowy Jork: Knopf. Numer ISBN 0-679-45443-8.
• Rudin, Walter (1987). Analiza rzeczywista i złożona . Nowy Jork: McGraw-Hill. Numer ISBN 0-07-100276-6.

Zewnętrzne linki

• „Sfera Riemanna” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• Moebius Transformations Revealed , Douglas N. Arnold i Jonathan Rogness (nagranie wideo dwóch profesorów University of Minnesota wyjaśniające i ilustrujące transformacje Möbiusa za pomocą projekcji stereograficznej ze sfery)