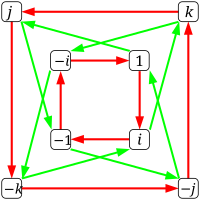
Tabliczka mnożenia grup Quaternion (forma uproszczona)
|
|
1
|
i
|
J
|
k
|
|
1
|
1
|
i
|
J
|
k
|
|
i
|
i
|
-1
|
k
|
− j
|
|
J
|
J
|
− k
|
-1
|
i
|
|
k
|
k
|
J
|
− ja
|
-1
|

Schemat cyklu Q
8 . Każdy kolor określa szereg potęg dowolnego elementu połączonego z elementem tożsamości e = 1. Na przykład cykl w kolorze czerwonym odzwierciedla fakt, że i
2 =
e , i
3 =
i oraz i
4 = e. Czerwony cykl odzwierciedla również to, że
i 2 =
e ,
i 3 = i oraz
i 4 = e.
W teorii grup The grupa kwaternion P 8 (czasami tylko oznaczona przez Q) jest nie abelowa grupę o kolejności osiem, izomorficzne z ośmiu elementów podzespołu
z quaternions pod mnożenia. Podaje go prezentacja grupowa

gdzie e jest elementem tożsamości, a e dojeżdża z innymi elementami grupy.
Kolejna prezentacja Q 8 to

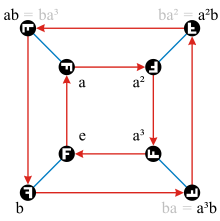
W porównaniu do grupy dwuściennej
Grupa kwaternionów Q 8 ma ten sam rząd jak grupa dwuścienna D 4 , ale inną strukturę, jak pokazują ich wykresy Cayleya i cyklu:
Na diagramach dla D 4 elementy grupy są oznaczone ich działaniem na literę F w reprezentacji definiującej R 2 . Tego samego nie można zrobić dla Q 8 , ponieważ nie ma wiernej reprezentacji w R 2 lub R 3 . D 4 może być zrealizowany jako podzbiór dzielonych quaternions w taki sam sposób, że Q 8 może być postrzegane jako podzbiór quaternions.
Stół Cayley
Tabeli Cayley (mnożenie tabela) Q 8 jest dana przez:
| × |
mi |
mi |
i |
i |
J |
J |
k |
k
|
| mi
|
mi |
mi |
i |
i |
J |
J |
k |
k
|
|
mi
|
mi |
mi |
i |
i |
J |
J |
k |
k
|
| i
|
i |
i |
mi |
mi |
k |
k |
J |
J
|
|
i
|
i |
i |
mi |
mi |
k |
k |
J |
J
|
| J
|
J |
J |
k |
k |
mi |
mi |
i |
i
|
|
J
|
J |
J |
k |
k |
mi |
mi |
i |
i
|
| k
|
k |
k |
J |
J |
i |
i |
mi |
mi
|
|
k
|
k |
k |
J |
J |
i |
i |
mi |
mi
|
Nieruchomości
Zauważ, że i , j i k mają w Q 8 porządek cztery, a dowolne dwa z nich generują całą grupę. Kolejna prezentacja Q 8 oparta tylko na dwóch elementach, aby pominąć tę nadmiarowość, to:

Można wziąć na przykład , i .


Grupa kwaternionów ma niezwykłą właściwość bycia hamiltonianem : Q 8 jest nieabelowa, ale każda podgrupa jest normalna . Każda grupa hamiltonowska zawiera kopię Q 8 .
Grupa kwaternion P 8 , a grupa D dwuścienny 4 są dwie najmniejsze przykłady nilpotent grupie bez Abelowych.
Centrum i podgrupa komutator Q 8 jest podgrupa . Wewnętrzna grupa automorfizmem Q 8 jest przez grupę modulo jego centrum, czyli grupa współczynnik Q 8 / {E, e }, która jest izomorficzny w Klein cztery grupy V. pełna grupa automorfizmem Q 8 jest izomorficzny do S 4 , symetryczna grupa na czterech literach (patrz reprezentacje macierzowe poniżej), a zewnętrzna grupa automorfizmu Q 8 jest więc S 4 /V, która jest izomorficzna z S 3 .

Grupa kwaternionów Q 8 ma pięć klas sprzężeń, { e }, { e }, { i, i }, { j, j }, { k, k }, a więc pięć nieredukowalnych reprezentacji nad liczbami zespolonymi o wymiarach 1, 1,1,1,2:
Trywialna reprezentacja
Reprezentacje znaków z jądrem i,j,k : Q 8 ma trzy maksymalne normalne podgrupy: podgrupy cykliczne generowane odpowiednio przez i, j oraz k. Dla każdej maksymalnej normalnej podgrupy N otrzymujemy jednowymiarową reprezentację faktoringową przez 2-elementową grupę ilorazową G / N . Reprezentacja wysyła elementy z N do 1, a elementy spoza N do -1.
Reprezentacja dwuwymiarowa : opisana poniżej w Reprezentacjach macierzy .
Tablica postaci w Q 8 okazuje się być taka sama jak w D 4 :
| Reprezentacja(ρ)/klasa sprzężeń |
{ e } |
{ e } |
{ ja, ja } |
{ j, j } |
{k, k }
|
| Trywialna reprezentacja |
1 |
1 |
1 |
1 |
1
|
| Reprezentacja znaku za pomocą i-kernel |
1 |
1 |
1 |
-1 |
-1
|
| Reprezentacja znaku za pomocą j-kernel |
1 |
1 |
-1 |
1 |
-1
|
| Reprezentacja znaku za pomocą k-kernel |
1 |
1 |
-1 |
-1 |
1
|
| reprezentacja dwuwymiarowa |
2 |
-2 |
0 |
0 |
0
|
Od nieredukowalnego znaków w wierszach powyżej mają wartości rzeczywiste, to daje rozkładu rzeczywistego grupowej algebry z do minimalnych dwustronnych ideałów : , gdzie idempotents odpowiadać na irreducibles: tak,

![{\ Displaystyle \ textstyle \ mathbb {R} [Q_ {8}] \ = \ \ bigoplus _ {\ rho} (e_ {\ rho})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1761120670b220c341d6011a5828e02fbea91465)
![{\ Displaystyle e_ {\ rho} \ w \ mathbb {R} [Q_ {8}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/998bce07bcab28516257658681275cfa3fa3565d)





 .
.
Każdy z tych nieredukowalnych ideałów jest izomorficzny z rzeczywistą centralną prostą algebrą , pierwsze cztery z ciałem rzeczywistym . Ostatnim idealny jest izomorficzna z pola skośnej z kwaterniony przez korespondencji:



Co więcej, homomorfizm projekcji podany przez ma ideał jądra wygenerowany przez idempotentnego:![{\ Displaystyle \ mathbb {R} [Q_ {8}] \ do (e_ {2}) \ cong \ mathbb {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed575d6fe2a2f4ad1b041497334d7e11f32fe5a3)


więc kwaterniony można również uzyskać jako pierścień ilorazu .
![{\ Displaystyle \ mathbb {R} [Q_ {8}] / (e + {\ bar {e}}) \ cong \ mathbb {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53ab95cc1e1943df7e6665e199487fb543252663)
Algebra grup zespolonych jest więc , gdzie jest algebrą bikwaternionów .
![{\ Displaystyle \ mathbb {C} [Q_ {8}] \ cong \ mathbb {C} ^ {\ oplus 4} \ oplus M_ {2} (\ mathbb {C})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86853166cd0baf213603720e72f18b1175ae519d)

Reprezentacje macierzowe

Tabliczka mnożenia grupy kwaternionów jako podgrupy
SL (2,
C ). Wpisy są reprezentowane przez sektory odpowiadające ich argumentom: 1 (zielony),
i (niebieski), -1 (czerwony), -
i (żółty).
Dwuwymiarowy nierozkładalny kompleks przedstawienie opisane powyżej daje grupy kwaternion Q 8 jako podgrupa ogólnym grupę liniową . Grupa kwaternionów jest multiplikatywną podgrupą algebry kwaternionów , która ma regularną reprezentację przez mnożenie od lewej , uważaną za złożoną przestrzeń wektorową z bazą , co odpowiada odwzorowaniu C - liniowemu . Wynikową reprezentację podaje:








Ponieważ wszystkie powyższe macierze mają wyznacznik jednostkowy, jest to reprezentacja Q 8 w specjalnej grupie liniowej SL(2, C ).
Wariant daje reprezentację przez macierze unitarne (tabela po prawej). Niech odpowiada odwzorowaniu liniowemu , czyli danemu przez:




Warto zauważyć, że fizycy używają wyłącznie innej konwencji reprezentacji macierzowej, aby nawiązać kontakt ze zwykłymi macierzami Pauliego :


Ten szczególny wybór jest wygodny i elegancki, gdy opisuje się stany spin-1/2 w bazie i uwzględnia operatory drabiny momentu pędu .



Tabliczka mnożenia grupy kwaternionów jako podgrupy
SL(2,3) . Elementy pola oznaczono 0,+,−.
Istnieje również ważne działanie Q 8 na dwuwymiarowej przestrzeni wektorowej nad polem skończonym F 3 = {0,1,−1} (tabela po prawej). Modułowy reprezentacja jest dana przez


Reprezentację tę można uzyskać z pola rozszerzenia F 9 = F 3 [ k ] = F 3 1 + F 3 k , gdzie k 2 = -1 i grupa multiplikatywna ( F 9 ) × ma generatory ±( k +1), ±( k -1) rzędu 8. Dwuwymiarowa przestrzeń F 3 -wektorowa F 9 dopuszcza liniowe odwzorowania dla z w F 9 , jak również automorfizm Frobeniusa spełniający i . Następnie powyższe macierze reprezentacji to , , , i .








Powyższy wykres realizuje Q 8 w normalnej podgrupy z GL (2, 3) . Zatem dla każdej macierzy , mamy automorfizm grup zdefiniowany przez , z . W rzeczywistości dają one pełną grupę automorfizmu jako: 



 ,
,
Jest izomorficzny grupa symetryczne S 4 od liniowego odwzorowania przestawianie cztery jednowymiarowe podprzestrzeni , to cztery punkty przestrzeni rzutowej .



Ponadto, ta reprezentacja permutacji osiem niezerowe wektory ( M 3 ) 2 , dając osadzanie Q 8 w grupie symetryczne S 8, oprócz zanurzeń podanych przez regularne reprezentacji.
Grupa Galois
Jak pokazał Richard Dean w 1981 roku, grupę kwaternionową można przedstawić jako grupę Galois Gal(T/ Q ), gdzie Q jest ciałem liczb wymiernych, a T jest ciałem rozszczepiającym nad Q wielomianu
-
 .
.
Opracowanie wykorzystuje fundamentalne twierdzenie teorii Galois przy określaniu czterech ciał pośrednich między Q i T oraz ich grupami Galois, a także dwa twierdzenia o cyklicznym rozszerzeniu stopnia czwartego nad ciałem.
Uogólniona grupa kwaternionów
Grupa uogólnione kwaternion P 4 N o uporządkowaniu 4, n jest określony przez przedstawienie

dla liczb całkowitych n ≥ 2 ze zwykłymi grupy kwaternionów podanej przez n = 2. Coxeter'a połączenia Q 4 n w dicykliczne grupy , w szczególnym przypadku binarnego grupy polihedryny i związanych z grupy polihedryny i dwuściennej grupy . Uogólniona grupa kwaternionów może być realizowana jako podgrupa generowana przez






gdzie . Może być również realizowany jako podgrupa kwaternionów jednostkowych generowanych przez i .



Uogólnione grupy kwaternionowe mają tę właściwość, że każda podgrupa abelowa jest cykliczna. Można wykazać, że skończona grupa p o tej właściwości (każda podgrupa abelowa jest cykliczna) jest albo cykliczna, albo uogólnioną grupą kwaternionową, jak zdefiniowano powyżej. Inną cechą charakterystyczną jest to, że skończona grupa p, w której występuje unikalna podgrupa rzędu p, jest albo cykliczna, albo dwugrupowa, izomorficzna z uogólnioną grupą kwaternionową. W szczególności, dla skończonego pola F o nieparzystej charakterystyce, podgrupa 2-Sylowa SL 2 ( F ) jest nieabelowa i ma tylko jedną podgrupę rzędu 2, więc ta podgrupa 2-Sylowa musi być uogólnioną grupą kwaternionową ( Gorenstein 1980 , s. 42). Niech p r będzie wielkością F , gdzie p jest liczbą pierwszą, rozmiar podgrupy 2-Sylowa SL 2 ( F ) wynosi 2 n , gdzie n = ord 2 ( p 2 − 1) + ord 2 ( r ) .
Twierdzenie Brauera-Suzukiego pokazuje, że grupy, których podgrupy Sylowa są uogólnionymi kwaternionami, nie mogą być proste.
Inna terminologia rezerwuje nazwę „uogólniona grupa kwaternionów” dla grupy dicyklicznej rzędu potęgi 2, która dopuszcza prezentację

Zobacz też
Uwagi
Bibliografia
-
Artin, Michael (1991), Algebra , Prentice Hall, ISBN 978-0-13-004763-2
-
Brown, Kenneth S. (1982), Cohomology grup (3rd ed.), Springer-Verlag, ISBN 978-0-387-90688-1
-
Cartan, Henri ; Eilenberg, Samuel (1999), Algebra Homologiczna , Princeton University Press, ISBN 978-0-691-04991-5
-
Coxeter, HSM i Moser, WOJ (1980). Generatory i relacje dla grup dyskretnych . Nowy Jork: Springer-Verlag. Numer ISBN 0-387-09212-9.
- Dean, Richard A. (1981) „Racjonalny wielomian, którego grupą są kwaterniony”, American Mathematical Monthly 88:42-5.
-
Gorenstein, D. (1980), Grupy skończone , New York: Chelsea, ISBN 978-0-8284-0301-6, MR 0569209
-
Johnson, David L. (1980), Tematy w teorii prezentacji grupowych , Cambridge University Press , ISBN 978-0-521-23108-4, MR 0695161
-
Rotman, Joseph J. (1995), Wprowadzenie do teorii grup (4 wyd.), Springer-Verlag, ISBN 978-0-387-94285-8
- PR Girard (1984) „Grupa kwaternionów i fizyka współczesna”, European Journal of Physics 5:25-32.
-
Hall, Marshall (1999), Teoria grup (wyd. 2), AMS Bookstore, ISBN 0-8218-1967-4
-
Kurosh, Alexander G. (1979), Teoria grup , AMS Bookstore, ISBN 0-8284-0107-1
Zewnętrzne linki















![{\ Displaystyle \ textstyle \ mathbb {R} [Q_ {8}] \ = \ \ bigoplus _ {\ rho} (e_ {\ rho})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1761120670b220c341d6011a5828e02fbea91465)
![{\ Displaystyle e_ {\ rho} \ w \ mathbb {R} [Q_ {8}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/998bce07bcab28516257658681275cfa3fa3565d)










![{\ Displaystyle \ mathbb {R} [Q_ {8}] \ do (e_ {2}) \ cong \ mathbb {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed575d6fe2a2f4ad1b041497334d7e11f32fe5a3)


![{\ Displaystyle \ mathbb {R} [Q_ {8}] / (e + {\ bar {e}}) \ cong \ mathbb {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53ab95cc1e1943df7e6665e199487fb543252663)
![{\ Displaystyle \ mathbb {C} [Q_ {8}] \ cong \ mathbb {C} ^ {\ oplus 4} \ oplus M_ {2} (\ mathbb {C})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86853166cd0baf213603720e72f18b1175ae519d)















































