Pierścień grupowy - Group ring

W Algebra , A pierścień grupa jest wolna moduł i w tym samym czasie koło , skonstruowane w sposób naturalny z dowolnego pierścienia i każdej grupie . Jako moduł swobodny, jego pierścień skalarów jest danym pierścieniem, a jego podstawą jest zbiór elementów danej grupy. Jako pierścień, jego prawo dodawania jest prawem modułu swobodnego, a jego mnożenie rozszerza „liniowo” dane prawo grupowe na podstawie. Mniej formalnie pierścień grupowy jest uogólnieniem danej grupy, poprzez przypisanie do każdego elementu grupy „współczynnika ważenia” z danego pierścienia.

Jeśli pierścień jest przemienny, to pierścień grupy jest również określany jako algebra grupy , ponieważ jest to rzeczywiście algebra nad danym pierścieniem. Algebra grup nad ciałem ma dalszą strukturę algebry Hopfa ; w tym przypadku nazywa się to algebrą grupową Hopfa .

Aparat pierścieni grupowych jest szczególnie przydatny w teorii reprezentacji grup .

Definicja

Niech G będzie grupą zapisaną multiplikatywnie, a R niech będzie pierścieniem. Pierścień grupy G przez R , co oznaczamy R [ G ] (lub po prostu RG ) jest zbiorem odwzorowań f  : G → R o skończonej wsparcia (f (g) jest różna od zera tylko skończoną wielu elementów g) , gdzie iloczyn skalarny modułu αf skalara α w R i odwzorowania f jest zdefiniowany jako odwzorowanie , a suma dwóch odwzorowań f i g w grupie modułów jest zdefiniowana jako odwzorowanie . Aby przekształcić grupę dodatków R [ G ] w pierścień, definiujemy iloczyn f i g jako odwzorowanie ${\ Displaystyle x \ mapsto \ alfa \ cdot f (x)}$${\ Displaystyle x \ mapsto f (x) + g (x)}$

${\ Displaystyle x \ mapsto \ suma _ {uv = x} f (u) g (v) = \ suma _ {u \ w G} f (u) g (u ^ {-1} x).}$

Podsumowanie jest uzasadnione, ponieważ f i g mają skończone wsparcie, a aksjomaty pierścienia można łatwo zweryfikować.

W użyciu są pewne odmiany notacji i terminologii. W szczególności odwzorowania takie jak f  : G → R są czasami zapisywane jako tak zwane „formalne liniowe kombinacje elementów G , ze współczynnikami w R ”:

${\ Displaystyle \ suma _ {g \ w G} f (g) g}$

lub po prostu

${\ Displaystyle \ suma _ {g \ w G} f_ {g} g}$

gdzie to nie powoduje zamieszania.

Należy zauważyć, że jeśli pierścień R jest w rzeczywistości polem K , to struktura modułowa pierścienia grupowego RG jest w rzeczywistości przestrzenią wektorową nad K .

Przykłady

1. Niech G = C ₃ , cykliczna grupa rzędu 3, z generatorem i elementem tożsamościowym 1 _G . Element r z C [ G ] można zapisać jako ${\displaystyle a}$

${\ Displaystyle r = z_ {0}1_ {G} + z_ {1} a + z_ {2} a ^ {2} \,}$

gdzie z ₀ , z ₁ i z ₂ są w C , liczbami zespolonymi . Jest to to samo co pierścień wielomianowy w zmiennej takiej, że np. C [ G ] jest izomorficzny z pierścieniem C [ ]/ . ${\displaystyle a}$${\ Displaystyle a ^ {3} = a ^ {0} = 1}$${\displaystyle a}$${\ Displaystyle (a ^ {3}-1)}$

Pisząc inny element s jako , ich suma to ${\displaystyle s=w_{0}1_{G}+w_{1}a+w_{2}a^{2}}$

${\ Displaystyle R + S = (Z_ {0}+ W_ {0}) 1_ {G} + (Z_ {1} + W_ {1}) A + (Z_ {2} + W_ {2}) A ^ {2} }\,}$

a ich produkt to

${\displaystyle rs=(z_{0}w_{0}+z_{1}w_{2}+z_{2}w_{1})1_{G}+(z_{0}w_{1}+z_{ 1}w_{0}+z_{2}w_{2})a+(z_{0}w_{2}+z_{2}w_{0}+z_{1}w_{1})a^{2} .}$

Zauważ, że element tożsamości 1 _G z G indukuje kanoniczne osadzenie pierścienia współczynnika (w tym przypadku C ) w C [ G ]; jednak ściśle mówiąc element tożsamości multiplikatywnej C [ G ] to 1⋅1 _{G ,} gdzie pierwsza 1 pochodzi z C , a druga z G . Element tożsamości dodatku wynosi zero.

Gdy G jest grupą nieprzemienną, należy uważać, aby zachować kolejność elementów grupy (i nie zamieniać ich przypadkowo) podczas mnożenia terminów.

2. Innym przykładem są wielomiany Laurenta nad pierścieniem R : nie są one niczym więcej lub mniej niż pierścieniem grupowym nieskończonej grupy cyklicznej Z nad R .

3. Niech Q będzie grupą kwaternionów z elementami . Rozważmy pierścień grupowy R Q , gdzie R jest zbiorem liczb rzeczywistych. Dowolny element tego pierścienia grupowego ma postać ${\ Displaystyle \ {e, {\ bar {e}}, ja, {\ bar {i}}, j, {\ bar {j}}, k, {\ bar {k}} \}}$

${\ Displaystyle x_ {1} \ cdot e + x_ {2} \ cdot {\ pasek {e}} + x_ {3} \ cdot i + x_ {4} \ cdot {\ pasek {i}} + x_ {5 }\cdot j+x_{6}\cdot {\bar {j}}+x_{7}\cdot k+x_{8}\cdot {\bar {k}}}$

gdzie jest liczba rzeczywista. ${\displaystyle x_{i}}$

Mnożenie, jak w każdym innym pierścieniu grupowym, jest definiowane na podstawie operacji grupowej. Na przykład,

${\ Displaystyle {\ zacząć {wyrównany} {\ duży (} 3 \ cdot e + {\ sqrt {2}} \ cdot ja {\ duży)} {\ duży (} {\ Frac {1} {2}} \ cdot {\bar {j}}{\big )}&=(3\cdot e)({\frac {1}{2}}\cdot {\bar {j}})+({\sqrt {2}} \cdot i)({\frac {1}{2}}\cdot {\bar {j}})\\&={\frac {3}{2}}\cdot {\big (}(e)( {\bar {j}}){\big )}+{\frac {\sqrt {2}}{2}}\cdot {\big (}(i)({\bar {j}}){\big )}\\&={\frac {3}{2}}\cdot {\bar {j}}+{\frac {\sqrt {2}}{2}}\cdot k\end{wyrównany}}. }$

Zauważ, że R Q to nie to samo, co pole skośne kwaternionów nad R . To dlatego, że pole ukosu Quaternions spełnia inne stosunki w pierścieniu, na przykład , podczas gdy w pierścieniu grupy R Q , nie jest równa . Mówiąc dokładniej, pierścień grupowy R Q ma wymiar 8 jako rzeczywista przestrzeń wektorowa , podczas gdy skośne pole kwaternionów ma wymiar 4 jako rzeczywista przestrzeń wektorowa . ${\displaystyle -1\cdot i=-i}$${\displaystyle -1\cdot i}$${\displaystyle 1\cdot {\bar {i}}}$

4. Innym przykładem nie Abelowych pierścienia grupowego jest , gdy jest grupa symetryczny 3 liter. Nie jest to domena integralna, ponieważ element jest transpozycją - permutacją, która zamienia tylko 1 i 2. Dlatego pierścień grupowy nie musi być domeną integralną, nawet jeśli podstawowy pierścień jest domeną integralną. ${\ Displaystyle \ mathbb {Z} [\ mathbb {S} _ {3}]}$${\ Displaystyle \ mathbb {S} _ {3}}$${\ Displaystyle [1-(12)] * [1 + (12)] = 1- (12) + (12) - (12) (12) = 1-1 = 0}$${\ Displaystyle (12) \ w \ mathbb {S} _ {3}}$

Niektóre podstawowe właściwości

Stosując 1 do oznaczenia multiplikatywnej identyczności pierścienia R i oznaczając jednostkę grupy przez 1 _G , pierścień R [ G ] zawiera podpierścień izomorficzny z R , a jego grupa elementów odwracalnych zawiera podgrupę izomorficzną z G . Do rozważenia funkcji wskaźnika {1 _G }, która jest wektorem f zdefiniowanym przez

${\ Displaystyle f (g) = 1 \ cdot 1_ {G} + \ suma _ {g \ nie = 1_ {G}} 0 \ cdot g = \ mathbf {1} _ {\ {1_ {G} \}} (g)={\begin{przypadki}1&g=1_{G}\\0&g\neq 1_{G}\end{przypadki}},}$

zbiór wszystkich skalarnych wielokrotności f jest podpierścieniem R [ G ] izomorficznym z R . A jeśli zmapujemy każdy element s z G na funkcję wskaźnika { s }, która jest wektorem f zdefiniowanym przez

${\ Displaystyle f (g) = 1 \ cdot s + \ suma _ {g \ nie = s} 0 \ cdot g = \ mathbf {1} _ {\ {s \}} (g) = {\ zacząć {przypadki} 1&g=s\\0&g\neq s\end{przypadki}}}$

wynikowe odwzorowanie jest homomorfizmem grupy iniektywnej (w odniesieniu do mnożenia, a nie dodawania, w R [ G ]).

Jeśli R i G są przemienne (tj. R jest przemienne, a G jest grupą abelową ), R [ G ] jest przemienne.

Jeśli H jest podgrupa o G , a R [ H ] jest podpierścień z R [ G ]. Podobnie, jeśli S jest podpierścieniem R , S [ G ] jest podpierścieniem R [ G ].

Jeśli G jest skończoną grupą rzędu większego niż 1, to R [ G ] zawsze ma dzielniki zerowe . Rozważmy na przykład element g rzędu G | g | = m > 1. Wtedy 1 - g jest dzielnikiem zera:

${\ Displaystyle (1-g) (1 + g + \ cdots + g ^ {m-1}) = 1 g ^ {m} = 1-1 = 0.}$

Rozważmy na przykład pierścień grupowy Z [ S ₃ ] i element rzędu 3 g =(123). W tym przypadku,

${\ Displaystyle (1-(123)) (1 + (123) + (132)) = 1- (123) ^ {3} = 1-1 = 0.}$

Powiązany wynik: Jeśli pierścień grupy jest liczbą pierwszą , wtedy G nie ma skończonej podgrupy normalnej o braku tożsamości (w szczególności G musi być nieskończona). ${\ Displaystyle K [G]}$

Dowód: Biorąc pod uwagę przeciwieństwo , załóżmy, że jest to podgrupa skończona normalna bez tożsamości . Weź . Ponieważ dla każdego , wiemy , zatem . Biorąc , mamy . Przez normalność , dojeżdża z podstawą , a zatem ${\ Displaystyle H}$${\ Displaystyle G}$${\ Displaystyle a = \ suma _ {h \ w H} h}$${\ Displaystyle hH = H}$${\ Displaystyle h \ w H}$${\displaystyle ha=a}$${\ Displaystyle a ^ {2} = \ suma _ {h \ w H} ha = | H | a}$${\displaystyle b=|H|\,1-a}$${\displaystyle ab=0}$${\ Displaystyle H}$${\displaystyle a}$${\ Displaystyle K [G]}$

${\ Displaystyle aK[G]b=K[G]ab=0}$.

I widzimy, że nie są zerami, co pokazuje, że nie jest liczbą pierwszą. To pokazuje oryginalne oświadczenie. ${\displaystyle a,b}$${\ Displaystyle K [G]}$

Algebra grup nad grupą skończoną

Algebrami grupy występują naturalnie w teorii reprezentacji grupy z grup skończonych . Algebra grupowa K [ G ] nad ciałem K jest zasadniczo pierścieniem grupowym, przy czym ciało K zajmuje miejsce pierścienia. Jako przestrzeń zbiorów i wektorów jest to wolna przestrzeń wektorowa na G nad ciałem K . Oznacza to, że dla x w K [ G ],

${\ Displaystyle x = \ suma _ {g \ w G} a_ {g} g.}$

Strukturę algebry na przestrzeni wektorowej definiuje się za pomocą mnożenia w grupie:

${\displaystyle g\cdot h=gh}$

w której po lewej stronie, g i h wskazują elementy Algebra grupowej podczas mnożenia na prawo jest operacja grupę (oznaczonej przez zestawienie).

Ponieważ powyższe mnożenia może być mylące, można również zapisać wektorów bazowych o K [ G ] w e _g (zamiast g ), w którym to przypadku mnożenie jest zapisana jako:

${\ Displaystyle e_ {g} \ cdot e_ {h} = e_ {gh}.}$

Interpretacja jako funkcje

Myśląc o wolnej przestrzeni wektorowej jako o funkcjach o wartościach K na G , mnożenie algebry jest splotem funkcji.

O ile algebra grupowa grupy skończonej może być utożsamiana z przestrzenią funkcji na grupie, o tyle dla grupy nieskończonej są one różne. Algebra grupowa, składająca się z sum skończonych , odpowiada funkcjom na grupie, które znikają o nieskończenie wiele punktów; topologicznie (przy użyciu topologii dyskretnej ) odpowiadają one funkcjom z obsługą zwartą .

Natomiast algebra grup K [ G ] i przestrzeń funkcji K ^G  := Hom( G , K ) są podwójne: dany element algebry grup

${\ Displaystyle x = \ suma _ {g \ w G} a_ {g} g}$

oraz funkcję na grupie f  : G → K te pary dają element K via

${\ Displaystyle (x, f) = \ suma _ {g \ w G} a_ {g} f (g)}$

co jest dobrze określoną sumą, ponieważ jest skończona.

Reprezentacje algebry grupowej

Biorąc K [ G ] za algebrę abstrakcyjną, można zapytać o reprezentacje algebry działającej na przestrzeni K- wektorowej V wymiaru d . Taka reprezentacja

${\displaystyle {\tylda {\rho}}:K[G]\rightarrow {\mbox {koniec}}(V)}$

jest homomorfizmem Algebra Algebra z grupy do algebry endomorfizm z V , który jest izomorficzny z pierścieniem d x d matryce: . Równoważnie jest to lewy moduł K [ G ] nad grupą abelową V . ${\ Displaystyle \ operatorname {koniec} (V) \ cong M_ {d} (K)}$

Odpowiednio, reprezentacja grupy

${\ Displaystyle \ rho : G \ rightarrow {\ mbox {Aut}} (V)}$

jest homomorfizmem grupowym od G do grupy automorfizmów liniowych V , który jest izomorficzny z ogólną grupą liniową macierzy odwracalnych: . Każda taka reprezentacja indukuje reprezentację algebry ${\ Displaystyle \ operatorname {Aut} (V) \ cong \ operatorname {GL} _ {d} (K)}$

${\displaystyle {\tylda {\rho}}:K[G]\rightarrow {\mbox {koniec}}(V)}$

po prostu pozwalając i rozszerzając się liniowo. Tak więc reprezentacje grupy odpowiadają dokładnie reprezentacjom algebry, a obie teorie są zasadniczo równoważne. ${\ Displaystyle {\ tylda {\ rho}} (e_ {g}) = \ rho (g)}$

Regularna reprezentacja

Algebra grupowa jest algebrą samą w sobie; pod korespondencją reprezentacji nad modułami R i R [ G ] jest to regularna reprezentacja grupy.

Zapisana jako reprezentacja, jest to reprezentacja g ↦ ρ _g z działaniem podanym przez , lub ${\ Displaystyle \ rho (g) \ cdot e_ {h} = e_ {gh}}$

${\ Displaystyle \ rho (g) \ cdot r = \ suma _ {h \ w G} k_ {h} \ rho (g) \ cdot e_ {h} = \ suma _ {h \ w G} k_ {h} e_{gh}.}$

Półprosty rozkład

Wymiar przestrzeni wektorowej K [ G ] jest po prostu równy liczbie elementów w grupie. Za ciało K powszechnie uważa się liczby zespolone C lub liczby rzeczywiste R , tak że omawiamy algebry grupowe C [ G ] lub R [ G ].

Algebra grupowa C [ G ] skończonej grupy nad liczbami zespolonymi jest pierścieniem półprostym . Wynik tego twierdzenia MASCHKE jest , pozwala zrozumieć C [ G ] w postaci skończonego produktu z pierścieni matrycy z wpisami C . W istocie, jeśli wymienione złożonych nieredukowalnych reprezentacji z G jako V _k o k = 1,. . . , m , odpowiadają one homomorfizmom grup , a więc homomorfizmom algebr . Złożenie tych odwzorowań daje izomorfizm algebry${\ Displaystyle \ rho _ {k}: G \ do \ operatorname {Aut} (V_ {k})}$${\ Displaystyle {\ tylda {\ rho}} _ {k}: \ mathbb {C} [G] \ do \ operatorname {koniec} (V_ {k})}$

${\ Displaystyle {\ tylda {\ rho}}: \ mathbb {C} [G] \ do \ bigoplus _ {k = 1} ^ {m} \ operatorname {koniec} (V_ {k}) \ cong \ bigoplus _ {k=1}^{m}M_{d_{k}}(\mathbb {C}),}$

gdzie d _k jest wymiarem V _k . Podalgebra C [ G ] odpowiadająca End( V _k ) jest dwustronnym ideałem generowanym przez idempotentnego

${\ Displaystyle \ epsilon _ {k} = {\ Frac {d_ {k}} {| G |}} \ suma _ {g \ w G} \ chi _ {k} (g ^ {-1}) \, g,}$

gdzie jest znak od V _k . Tworzą one kompletny system ortogonalnych idempotentów, tak że , dla j ≠ k , oraz . Izomorfizm jest ściśle związany z transformacją Fouriera na grupach skończonych . ${\ Displaystyle \ chi _ {k} (g) = \ operatorname {tr} \ \ rho _ {k} (g)}$${\ Displaystyle \ epsilon _ {k} ^ {2} = \ epsilon _ {k}}$${\ Displaystyle \ epsilon _ {j} \ epsilon _ {k} = 0}$${\ Displaystyle 1 = \ epsilon _ {1} + \ cdots + \ epsilon _ {m}}$${\displaystyle {\tylda {\rho}}}$

W przypadku bardziej ogólnym polu K, gdy charakterystyka z K nie dzieli uporządkowanie grupy G , a K [ G ] oznacza półprosty. Gdy G jest skończoną grupą abelową , pierścień grupy K [G] jest przemienny, a jego strukturę można łatwo wyrazić w kategoriach pierwiastków jedności .

Gdy K jest polem charakterystyki p , które dzieli rząd G , pierścień grupowy nie jest półprosty: ma niezerowy rodnik Jacobsona , co nadaje odpowiedniemu podmiotowi modularnej teorii reprezentacji jego własny, głębszy charakter.

Środek algebry grupowej

Centrum algebry grupowej to zbiór elementów, które dojeżdżają z wszystkich elementów algebry grupowej:

${\ Displaystyle \ operatorname {Z} (K [G]): = \ lewo \ {z \ w K [G]: \ forall r \ w K [G], zr = rz \ po prawej \}.}$

Centrum jest równe zbiorowi funkcji klasy , czyli zbiorowi elementów, które są stałe na każdej klasie sprzężeń

${\ Displaystyle \ operatorname {Z} (K [G]) = \ lewo \ {\ suma _ {g \ w G} a_ {g} g: \ forall g, h \ w G, a_ {g} = a_ { h^{-1}gh}\prawo\}.}$

Jeżeli K = C , zestaw nieredukowalnych znaków o G tworzy podstawę ortonormalną z Z ( K [ G ]), w odniesieniu do produktu wewnętrzną

${\ Displaystyle \ lewo \ langle \ suma _ {g \ w G} a_ {g} g \ suma _ {g \ w G} b_ {g} g \ prawo \ rangle = {\ Frac {1} {| G |}}\suma _{g\w G}{\bar {a}}_{g}b_{g}.}$

Grupa dzwoni do nieskończonej grupy

Znacznie mniej wiadomo w przypadku, gdy G jest przeliczalnie nieskończone lub niepoliczalne i jest to obszar aktywnych badań. Przypadek, w którym R jest ciałem liczb zespolonych, jest prawdopodobnie najlepiej zbadany. W tym przypadku, Irving Kaplansky okazało się, że jeśli i b są elementami C, [ G ] W AB = 1 , a ba = 1 . Nie wiadomo, czy tak jest, jeśli R jest polem o dodatniej charakterystyce.

Długoletnia hipoteza Kaplansky'ego (~1940) mówi, że jeśli G jest grupą wolną od skręcania , a K jest polem, to pierścień grupy K [ G ] nie ma nietrywialnych dzielników zera . Ta hipoteza jest równoważna K [ G ] nie mającej nietrywialnych nilpotentów w ramach tych samych hipotez dla K i G .

W rzeczywistości warunek, że K jest polem, można rozluźnić do dowolnego pierścienia, który może być osadzony w domenie integralnej .

Przypuszczenie pozostaje otwarte w pełnej ogólności, jednak wykazano, że niektóre szczególne przypadki grup wolnych od skręcania spełniają przypuszczenie zerowego dzielnika. Obejmują one:

• Unikalne grupy produktów (np. grupy zamawiane , w szczególności bezpłatne grupy )
• Podstawowe grupy dające się ująć (np. grupy wirtualnie abelowe )
• Grupy rozproszone – w szczególności grupy, które działają swobodnie izometrycznie na drzewach R oraz podstawowe grupy grup powierzchniowych z wyjątkiem grup podstawowych o sumach bezpośrednich jednej, dwóch lub trzech kopii płaszczyzny rzutowej.

Przypadek, w którym G jest grupą topologiczną, został szerzej omówiony w artykule Algebra grup lokalnie zwartej grupy .

Teoria kategorii

Przylegający

Kategorycznie , konstrukcja pierścienia grupowego jest połączona z „ grupą jednostek ”; sprzężoną parą są następujące funktory :

${\ Displaystyle R [-] \ dwukropek \ mathbf {grp} \ do R \ mathbf {{\ tekst {-}} Alg}}$

${\ Displaystyle (-) ^ {\ razy} \ dwukropek R \ mathbf {{\ tekst {-}} Alg} \ do \ mathbf {grp}}$

gdzie przenosi grupę do swojej grupy pierścieniem nad R , i przenosi R -algebrę do swojej grupy jednostek. ${\displaystyle R[-]}$${\ Displaystyle (-) ^ {\ razy}}$

Gdy R = Z , daje to dodatek między kategorią grup a kategorią pierścieni , a jednostka dodatku przenosi grupę G do grupy zawierającej jednostki trywialne: G × {±1} = {± g }. Na ogół pierścienie grupowe zawierają nietrywialne jednostki. Jeśli G zawiera elementy a i b takie, że i b nie normalizują, to kwadrat ${\ Displaystyle a ^ {n} = 1}$${\displaystyle \langle a\rangle}$

${\ Displaystyle x = (a-1) b \ lewo (1 + a + a ^ {2} + ... + a ^ {n-1} \ prawej)}$

wynosi zero, stąd . Element 1 + x jest jednostką nieskończonego porządku. ${\ Displaystyle (1 + x) (1-x) = 1}$

Własność uniwersalna

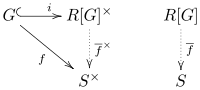
Powyższy dodatek wyraża uniwersalną właściwość pierścieni grupowych. Niech R być przemienne (pierścień), niech G jest grupą, niech S być R -algebra. Dla homomorfizmu każdej grupy istnieje unikalny homomorfizm R- algebry taki, że gdzie i jest inkluzją ${\ Displaystyle f: G \ do S ^ {\ razy}}$${\displaystyle {\overline {f}}:R[G]\do S}$${\displaystyle {\overline {f}}\circ i=f}$

${\ Displaystyle {\ zacząć {wyrównany} ja: G & \ longrightarrow R [G] \ \ g i \ longmapsto 1_ {R} g \ koniec {wyrównany}}}$

Innymi słowy, jest unikalnym homomorfizmem, który powoduje, że następujący diagram komutuje: ${\displaystyle {\overline {f}}}$

Każdy inny pierścień spełniający tę właściwość jest kanonicznie izomorficzny z pierścieniem grupowym.

Algebra Hopfa

Algebra grup K [ G ] ma naturalną strukturę algebry Hopfa . Komultiplikacja jest zdefiniowana przez , rozciągnięta liniowo, a antypoda jest ponownie rozciągnięta liniowo. ${\ Displaystyle \ Delta (g) = g \ czasami g}$${\ Displaystyle S (g) = g ^ {-1}}$

Uogólnienia

Algebra grupowa uogólnia się do pierścienia monoidalnego , a stąd do algebry kategorii , której innym przykładem jest algebra incydencji .

Filtrowanie

Jeśli grupa ma funkcję długości — na przykład, jeśli istnieje wybór generatorów i bierze się słowo metric , jak w grupach Coxetera — wówczas pierścień grupy staje się algebrą filtrowaną .

Zobacz też

• Algebra grupowa grupy lokalnie zwartej
• Pierścień monoidowy

Teoria reprezentacji

• Reprezentacja grupy
• Regularna reprezentacja

Teoria kategorii

• Algebra kategorialna
• Grupa jednostek
• Algebra incydentów
• Algebra kołczanowa

Uwagi

Bibliografia

• AA Bovdi (2001) [1994], "Algebra grupowa" , Encyklopedia Matematyki , EMS Press
• Milies, César Polcino; Sehgal, Sudarshan K. Wprowadzenie do kręgów grupowych . Algebry i zastosowania, tom 1. Springer, 2002. ISBN  978-1-4020-0238-0
• Charles W. Curtis , Irving Reiner . Teoria reprezentacji grup skończonych i algebr asocjacyjnych , Interscience (1962)
• DS Passman, Struktura algebraiczna pierścieni grupowych , Wiley (1977)