Zwijanie (matematyka) - Curl (mathematics)

W rachunku wektorowego The curl jest operator wektor , który opisuje nieskończenie krążenie o pola wektorowego w trójwymiarowej przestrzeni euklidesowej . Zakręt w punkcie pola jest reprezentowany przez wektor, którego długość i kierunek oznaczają wielkość i oś maksymalnego krążenia. Skręt pola jest formalnie definiowany jako gęstość cyrkulacji w każdym punkcie pola.

Pole wektorowe, którego rotacja wynosi zero, nazywa się nierotacyjnym . Curl jest formą różnicowania pól wektorowych. Odpowiednią formą podstawową twierdzenia rachunku jest twierdzenie Stokesa , który odnosi się do powierzchni całkowej z zawiniętym pola wektorowego do całki linii w polu wektorowym wokół krzywej granicznej.

Alternatywna terminologia rotacja lub rotacyjna i alternatywna notacja rot F lub iloczyn krzyżowy z operatorem del (nabla) ∇ × F są czasami używane do curl F . Norma ISO / IEC 80000-2 zaleca stosowanie zgnilizny zapisie pogrubioną czcionką w przeciwieństwie do curl notacji.

W przeciwieństwie do gradientu i dywergencji rotacja sformułowana w rachunku wektorowym nie uogólnia po prostu innych wymiarów; możliwe są pewne uogólnienia , ale tylko w trzech wymiarach geometrycznie określony rotacja pola wektorowego jest ponownie polem wektorowym. Ten niedobór jest bezpośrednią konsekwencją ograniczeń rachunku wektorów; wyrażony za pomocą operatora klina rachunku geometrycznego, rotacja uogólnia się na wszystkie wymiary. Niefortunna okoliczność jest podobna do tej, która towarzyszy trójwymiarowemu iloczynowi krzyżowemu , i rzeczywiście połączenie jest odzwierciedlone w zapisie ∇× dla krzywizny.

Nazwa „zawinięcie” została po raz pierwszy zasugerowana przez Jamesa Clerka Maxwella w 1871 roku, ale koncepcja ta została najwyraźniej po raz pierwszy użyta w konstrukcji teorii pola optycznego przez Jamesa MacCullagha w 1839 roku.

Definicja

Krzywizna pola wektorowego F , oznaczana przez rotację F , lub ∇ × F , lub rot F , w punkcie jest definiowana w kategoriach rzutowania na różne linie przechodzące przez punkt. Jeśli jest dowolnym wektorem jednostkowym, rzut krzywizny F na jest zdefiniowany jako wartość graniczna całki zamkniętej w płaszczyźnie prostopadłej do podzielonej przez obszar zamknięty, ponieważ ścieżka integracji jest skrócona wokół punktu. ${\ Displaystyle \ mathbf {\ kapelusz {n}}}$${\ Displaystyle \ mathbf {\ kapelusz {n}}}$${\ Displaystyle \ mathbf {\ kapelusz {n}}}$

Operator curl odwzorowuje ciągle różniczkowalne funkcje f  : R ³ → R ³ na funkcje ciągłe g  : R ³ → R ³ , aw szczególności odwzorowuje funkcje C ^k w R ³ na funkcje C ^{k -1} w R ³ .

Domyślnie curl jest zdefiniowany w punkcie p as

${\ Displaystyle (\ nabla \ razy \ mathbf {f} ) (p) \ cdot \ mathbf {\ kapelusz {n}} \ {\ przesunięty {\ zaniżony {\ operatorname {def}}} {{} = { }}}\lim _{A\to 0}{\frac {1}{|A|}}\oint _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {r} }$

gdzie integralną linia jest liczona wzdłuż granicznej C w strefie A w pytaniu | | wielkość obszaru. To równanie definiuje rzut krzywizny F na . Nieskończenie małe powierzchnie ograniczone przez C mają jako normalne . C jest zorientowany za pomocą reguły prawej ręki . ${\ Displaystyle \ mathbf {\ kapelusz {n}}}$${\ Displaystyle \ mathbf {\ kapelusz {n}}}$

Powyższe oznacza, że wzór zwijającego pola wektorowego jest zdefiniowane jako nieskończenie gęstość powierzchniową w obiegu tej dziedzinie. Do tej definicji pasuje naturalnie

• twierdzenie Kelvina-Stokesa jako globalny wzoru, zgodnie z definicją, a
• następującą "łatwą do zapamiętania" definicję krzywizny we współrzędnych ortogonalnych krzywoliniowych , np. we współrzędnych kartezjańskich , sferycznych , cylindrycznych , a nawet eliptycznych lub parabolicznych :

  ${\ Displaystyle {\ zacząć {wyrównany} i (\ nazwa operatora {curl} \ mathbf {F} ) _ {1} = {\ Frac {1} {h_ {2} h_ {3}}} \ lewo ({\ Frac {\partial (h_{3}F_{3})}{\partial u_{2}}}-{\frac {\partial (h_{2}F_{2})}{\partial u_{3}}} \right),\\[5pt]&(\operatorname {curl} \mathbf {F} )_{2}={\frac {1}{h_{3}h_{1}}}\left({\frac {\partial (h_{1}F_{1})}{\partial u_{3}}}-{\frac {\partial (h_{3}F_{3})}{\partial u_{1}}} \right),\\[5pt]&(\operatorname {curl} \mathbf {F} )_{3}={\frac {1}{h_{1}h_{2}}}\left({\frac {\partial (h_{2}F_{2})}{\partial u_{1}}}-{\frac {\partial (h_{1}F_{1})}{\partial u_{2}}} \right).\end{wyrównany}}}$

Równanie dla każdego składnika (zwijanie F ) _k można uzyskać zamieniając każde wystąpienie indeksu dolnego 1, 2, 3 w permutacji cyklicznej: 1 → 2, 2 → 3 i 3 → 1 (gdzie indeksy dolne reprezentują odpowiednie indeksy) .

Jeżeli ( x ₁ , x ₂ , x ₃ ) są współrzędnymi kartezjańskimi i ( u ₁ , u ₂ , u ₃ ) są współrzędnymi ortogonalnymi, to

${\ Displaystyle h_ {i} = {\ sqrt {\ lewo ({\ Frac {\ częściowy x_ {1}} {\ częściowy u_ {i}}} \ po prawej) ^ {2} + \ lewo ({\ Frac { \partial x_{2}}{\partial u_{i}}}\right)^{2}+\left({\frac {\partial x_{3}}{\partial u_{i}}}\right) ^{2}}}}$

jest długością wektora współrzędnych odpowiadającego u _i . Pozostałe dwa składniki wyniku zwijanie cyklicznego permutacji o indeksach : 3,1,2 → 1,2,3 → 2,3,1.

Intuicyjna interpretacja

Załóżmy, że pole wektorowe opisuje pola prędkości o przepływu płynu (na przykład, jak duży zbiornik na ciecz lub gaz ), a kulka znajduje się w cieczy lub gazu (środek kuli jest zamocowany w określonym punkcie). Jeśli kula ma chropowatą powierzchnię, przepływający przez nią płyn spowoduje jej obrót. Oś obrotu (zorientowana zgodnie z regułą prawej ręki) wskazuje kierunek zawinięcia pola w środku kuli, a prędkość kątowa obrotu jest równa połowie wielkości zawinięcia w tym punkcie.

Zawinięcie wektora w każdym momencie jest przez obrót przestrzeni nieskończenie w xy -plane (dla Z -osiowy składnik curl) zx -plane (dla R -osiowy składnik curl) i YZ -plane (dla składnika osi x wektora zwinięcia). Widać to wyraźnie na poniższych przykładach.

Stosowanie

W praktyce powyższa definicja jest rzadko używana, ponieważ praktycznie we wszystkich przypadkach operator curl może być zastosowany przy użyciu pewnego zestawu współrzędnych krzywoliniowych , dla których wyprowadzono prostsze reprezentacje.

Notacja ∇ × F ma swoje początki w podobieństwach do trójwymiarowego produktu krzyżowego i jest użyteczna jako mnemonik we współrzędnych kartezjańskich, jeśli ∇ jest traktowane jako wektorowy operator różniczkowy del . Taka notacja z operatorami jest powszechna w fizyce i algebrze .

Rozszerzony w trójwymiarowe współrzędne kartezjańskie (patrz Del we współrzędnych cylindrycznych i sferycznych dla reprezentacji współrzędnych sferycznych i cylindrycznych ), ∇ × F jest, dla F składa się z [ F _x , F _y , F _z ] (gdzie indeksy wskazują składowe wektor, a nie pochodne cząstkowe):

${\ Displaystyle \ nabla \ razy \ mathbf {F} = {\ zacząć {vmatrix} {\ boldsymbol {\ kapelusz {\ imata}}} i {\ boldsymbol {\ kapelusz {\ jmath}}} i {\ boldsymbol {\ kapelusz {k}}}\\[5pt]{\dfrac {\częściowy }{\częściowy x}}&{\dfrac {\częściowy }{\częściowy y}}&{\dfrac {\częściowy }{\częściowy z }}\\[10pt]F_{x}&F_{y}&F_{z}\end{vmatrix}}}$

gdzie I , J i K są wektor jednostkowy dla X -,, r -, i Z -axes, odpowiednio. To rozwija się w następujący sposób:

${\ Displaystyle \ nabla \ razy \ mathbf {F} = \ lewo ({\ Frac {\ częściowy F_ {Z}} {\ częściowy Y}} - {\ Frac {\ częściowy F_ {y}} {\ częściowy Z} }\right){\boldsymbol {\hat {\imath }}}+\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{ \partial x}}\right){\boldsymbol {\hat {\jmath }}}+\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{ x}}{\częściowy y}}\right){\boldsymbol {\hat {k}}}={\begin{bmatrix}{\frac {\częściowy F_{z}}{\częściowy y}}-{\ frac {\częściowy F_{y}}{\częściowy F_{z}\\{\frac {\częściowy F_{x}}{\częściowy z}}-{\frac {\częściowy F_{z}}{\częściowy x }}\\{\frac {\częściowy F_{y}}{\częściowy x}}-{\frac {\częściowy F_{x}}{\częściowy y}}\end{bmatrix}}}$

Chociaż wyrażony w postaci współrzędnych, wynik jest niezmienny przy odpowiednich obrotach osi współrzędnych, ale wynik jest odwracany przy odbiciu.

W ogólnym układzie współrzędnych rotacja jest wyrażona wzorem

${\ Displaystyle (\ nabla \ razy \ mathbf {F} ) ^ {k} = {\ Frac {1} {\ sqrt {g}}} \ varepsilon ^ {k \ ell m} \ nabla _ {\ ell} F_ {m}}$

gdzie ε oznacza tensor Levi-Civita , ∇ pochodna kowariantna , jest Jacobiego i konwencja podsumowanie Einsteina wynika, że powtarzające się indeksy są zsumowane. Ze względu na symetrię symboli Christoffela uczestniczących w pochodnej kowariantnej wyrażenie to sprowadza się do pochodnej cząstkowej: ${\displaystyle {\sqrt {g}}}$

${\ Displaystyle (\ nabla \ razy \ mathbf {F} ) = {\ Frac {1} {\ sqrt {g}}} \ mathbf {R} _ {k} \ varepsilon ^ {k \ ell m} \ częściowy _ {l}F_{m}}$

gdzie R _k są lokalnymi wektorami bazowymi. Odpowiednio, używając zewnętrznej pochodnej , rotacja może być wyrażona jako:

${\ Displaystyle \ nabla \ razy \ mathbf {f} = \ lewo (\ gwiazda {\ duży (}{\ operatorname {d}} \ mathbf {f} ^ {\ płaski} {\ duży)} \ prawej) ^ { \ostry }}$

Tutaj ♭ i ♯ to muzyczne izomorfizmy , a ★ to operator gwiazdy Hodge'a . Ten wzór pokazuje, jak obliczyć rotację F w dowolnym układzie współrzędnych i jak rozszerzyć rotację na dowolną zorientowaną trójwymiarową rozmaitość Riemanna . Ponieważ zależy to od wyboru orientacji, zwijanie jest operacją chiralną . Innymi słowy, jeśli orientacja jest odwrócona, kierunek zawinięcia również jest odwrócony.

Przykłady

Przykład 1

Pole wektorowe

${\ Displaystyle \ mathbf {F} (x, y, z) = y {\ boldsymbol {\ kapelusz {\ imat}}}-x {\ boldsymbol {\ kapelusz {\ jmath}}}}$

można rozłożyć jako

${\ Displaystyle \ mathbf {F} _ {x} = y \ mathbf {F} _ {y} = -x \ mathbf {F} _ {z} = 0.}$

Po oględzinach pole można opisać jako „obracające się”. Gdyby wektory pola reprezentowały siłę liniową działającą na obiekty znajdujące się w tym punkcie, a obiekt miałby zostać umieszczony wewnątrz pola, obiekt zacząłby się obracać wokół siebie zgodnie z ruchem wskazówek zegara. Dzieje się tak niezależnie od tego, gdzie znajduje się obiekt.

Obliczanie loków:

${\ Displaystyle \ nabla \ razy \ mathbf {F} = 0 {\ boldsymbol {\ kapelusz {\ imat}}} + 0 {\ boldsymbol {\ kapelusz {\ jmath}}} + \ lewo ({\ Frac {\ częściowy }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right){\boldsymbol {\hat {k}}}=-2{\boldsymbol {\hat { k}}}}$

Wynikowe pole wektorowe opisujące zwijanie byłoby we wszystkich punktach skierowane w ujemnym kierunku z . Wyniki tego równania są zgodne z tym, co można było przewidzieć za pomocą reguły prawej ręki przy użyciu prawoskrętnego układu współrzędnych . Będąc jednolitym polem wektorowym, opisany wcześniej obiekt miałby taką samą intensywność rotacji niezależnie od tego, gdzie zostałby umieszczony.

Przykład 2

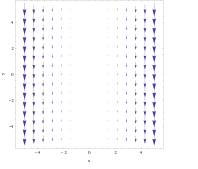
Dla pola wektorowego

${\ Displaystyle \ mathbf {F} (x, y, z) = - x ^ {2} {\ pogrubiony symbol {\ kapelusz {\ jmath}}}}$

zwijanie nie jest tak oczywiste z wykresu. Jednak biorąc obiekt z poprzedniego przykładu i umieszczając go w dowolnym miejscu na linii x = 3 , siła wywierana na prawą stronę byłaby nieco większa niż siła wywierana na lewą, powodując jego obrót zgodnie z ruchem wskazówek zegara. Stosując regułę prawej ręki, można przewidzieć, że wynikowe zawinięcie będzie proste w ujemnym kierunku z . Odwrotnie, jeśli zostanie umieszczony na x = −3 , obiekt obróci się w kierunku przeciwnym do ruchu wskazówek zegara, a reguła prawej ręki dałaby dodatni kierunek z .

Obliczanie loków:

${\displaystyle {\nabla}\razy \mathbf {F} =0{\boldsymbol {\kapelusz {\imath}}}+0{\boldsymbol {\kapelusz {\jmath}}}+{\frac {\częściowy} {\partial x}}\left(-x^{2}\right){\boldsymbol {\hat {k}}}=-2x{\boldsymbol {\hat {k}}}.}$

Zakręt wskazuje w ujemnym kierunku z, gdy x jest dodatnie i na odwrót. W tym polu intensywność rotacji byłaby większa w miarę oddalania się obiektu od płaszczyzny x = 0 .

Przykłady opisowe

• W polu wektorowym opisującym liniowe prędkości każdej części wirującego dysku, rotacja ma tę samą wartość we wszystkich punktach.
• Spośród czterech równań Maxwella , dwu- prawo Faradaya i prawo Ampera -może być zwięźle wyrażony za pomocą curl. Prawo Faradaya mówi, że rotacja pola elektrycznego jest przeciwna do szybkości zmian pola magnetycznego w czasie, podczas gdy prawo Ampère'a wiąże rotację pola magnetycznego z prądem i szybkością zmiany pola elektrycznego.

Tożsamości

W ogólnych współrzędnych krzywoliniowych (nie tylko we współrzędnych kartezjańskich) można wykazać , że rotacja iloczynu poprzecznego pól wektorowych v i F jest

${\ Displaystyle \ nabla \ razy \ lewo (\ mathbf {v \ razy F} \ prawej) = {\ duży (} \ lewo (\ mathbf {\ nabla \ cdot F} \ prawej) + \ mathbf {f \ cdot \ nabla } {\duża )}\mathbf {v} -{\duża (}\left(\mathbf {\nabla \cdot v} \right)+\mathbf {v\cdot \nabla } {\duża )}\mathbf {F} \ .}$

Zamieniając operator pola wektorowego v i ∇ , otrzymujemy iloczyn krzyżowy pola wektorowego z rotacją pola wektorowego:

${\ Displaystyle \ mathbf {v \ \ razy} \ po lewej (\ mathbf {\ nabla \ razy F} \ prawej) = \ nabla _ {\ mathbf {f}} \ po lewej (\ mathbf {v \ cdot F} \ prawej) )-\left(\mathbf {v\cdot \nabla } \right)\mathbf {F} \ ,}$

gdzie ∇ _F jest notacją w indeksie dolnym Feynmana, która uwzględnia tylko zmienność spowodowaną polem wektorowym F (tj. w tym przypadku v jest traktowane jako stałe w przestrzeni).

Innym przykładem jest rotacja rotacji pola wektorowego. Można wykazać, że we współrzędnych ogólnych

${\ Displaystyle \ nabla \ razy \ lewo (\ mathbf {\ nabla \ razy F} \ po prawej) = \ mathbf {\ nabla} (\ mathbf {\ nabla \ cdot F}) - \ nabla ^ {2} \ mathbf { F} \ ,}$

i Tożsamość określa Laplace'a wektor z F , oznaczany ∇ ² F .

Zawinięcie z gradientem od każdej skalarnego pola cp jest zawsze zerową wektora pola

${\ Displaystyle \ nabla \ razy (\ nabla \ varphi) = {\ pogrubiony symbol {0}}}$

co wynika z antysymetrii w definicji rotacji i symetrii drugich pochodnych .

Jeśli φ jest funkcją o wartościach skalarnych, a F jest polem wektorowym, to

${\ Displaystyle \ nabla \ razy (\ varphi \ mathbf {f} ) = \ nabla \ varphi \ razy \ mathbf {f} + \ varphi \ nabla \ razy \ mathbf {f}}$

Uogólnienia

Operacje na rachunku wektorowym grad , curl i div są najłatwiejsze do uogólnienia w kontekście form różniczkowych, co obejmuje kilka kroków. Krótko mówiąc, odpowiadają one pochodnym, odpowiednio, 0-form, 1-form i 2-form. Geometryczna interpretacja rotacji jako rotacji odpowiada identyfikacji dwuwektorów (2-wektorów) w 3 wymiarach za pomocą specjalnej ortogonalnej algebry Liego (3) nieskończenie małych obrotów (we współrzędnych, skośno-symetryczne macierze 3 × 3), podczas gdy reprezentacja obrotów przez wektory odpowiada do identyfikacji 1-wektorów (odpowiednik 2-wektorów) i (3) , które są przestrzeniami 3-wymiarowymi. ${\displaystyle {\mathfrak {tak}}}$${\displaystyle {\mathfrak {tak}}}$

Formy różniczkowe

W 3 wymiarach forma różniczkowa 0 jest po prostu funkcją f ( x , y , z ) ; forma różniczkowa 1 jest następującym wyrażeniem, w którym współczynniki są funkcjami:

${\displaystyle a_{1}\,dx+a_{2}\,dy+a_{3}\,dz;}$

forma różniczkowa 2 jest sumą formalną, ponownie ze współczynnikami funkcji:

${\ Displaystyle a_ {12} \ dx \ klin dy + a_ {13} \ dx \ klin dz + a_ {23} \ dy \ klin dz;}$

a różniczkowa forma 3 jest zdefiniowana przez pojedynczy wyraz z jedną funkcją jako współczynnikiem:

${\ Displaystyle a_ {123} \ dx \ klin dy \ klin dz.}$

(W tym przypadku współczynniki a są rzeczywistymi funkcjami trzech zmiennych; „iloczyny klinowe”, np. dx ∧ dy , można interpretować jako pewien rodzaj zorientowanych elementów powierzchniowych, dx ∧ dy = − dy ∧ dx , itd.)

Zewnątrz pochodną o k postać a w R ³ jest zdefiniowany jako ( k + 1), postać a od góry, a R ⁿ , jeśli np

${\ Displaystyle \ omega ^ {(k)} = \ suma _ {\ scriptstyle {i_{1}<i_{2}<\cdots <i_{k}} \atop \forall \scriptstyle {i_{\nu}\ w 1,\ldots ,n}}a_{i_{1},\ldots ,i_{k}}\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{k}},}$

wtedy pochodna zewnętrzna d prowadzi do

${\ Displaystyle d \ omega ^ {(k)} = \ suma _ {\ scriptstyle {j = 1} \ atop \ scriptstyle {i_ {1}< \ cdots <i_ {k}}} ^ {n} {\ Frac {\partial a_{i_{1},\ldots ,i_{k}}}{\partial x_{j}}}\,dx_{j}\wedge dx_{i_{1}}\wedge \cdots \wedge dx_ {i_{k}}.}$

Zewnętrzna pochodna formy 1 jest zatem formą 2, a forma 2 jest formą 3 . Z drugiej strony ze względu na wymienność mieszanych instrumentów pochodnych, np. z powodu

${\ Displaystyle {\ Frac {\ częściowy ^ {2}} {\ częściowy x \ \ częściowy r}} = {\ Frac {\ częściowy ^ {2}} {\ częściowy r \ \ częściowy x}}}$

dwukrotne zastosowanie zewnętrznej pochodnej prowadzi do 0.

Zatem oznaczając przestrzeń k -form przez Ω ^k ( R ³ ) i pochodną zewnętrzną przez d otrzymujemy ciąg:

${\ Displaystyle 0 \, {\ overset {d}{\ longrightarrow }} \; \ Omega ^ {0} \ lewo (\ mathbb {R} ^ {3} \ prawo) \ {\ overset {d} {\ longrightarrow }}\;\Omega ^{1}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{2}\left( \mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{3}\left(\mathbb {R} ^{3}\right)\, {\overset {d}{\longrightarrow }}\,0.}$

Tutaj Ω ^k ( R ⁿ ) jest przestrzenią odcinków zewnętrznej algebry Λ ^k ( R ⁿ ) wiązki wektorów nad R ⁿ , której wymiarem jest współczynnik dwumianowy (ⁿ
_k) ; zauważ, żeΩ ^k ( R ³ ) = 0dla k > 3lub k < 0. Pisząc tylko wymiary, otrzymujemy rządtrójkąta Pascala:

0 → 1 → 3 → 3 → 1 → 0;

włókna jednowymiarowe odpowiadają polom skalarnym, a włókna trójwymiarowe polom wektorowym, jak opisano poniżej. Odpowiednie identyfikacje Modulo, trzy nietrywialne wystąpienia pochodnej zewnętrznej odpowiadają gradowi, rotacji i div.

Formy różniczkowe i różniczkę można zdefiniować na dowolnej przestrzeni euklidesowej, a nawet na dowolnej rozmaitości, bez żadnego pojęcia metryki riemannowskiej. Na Riemanna kolektora , albo bardziej ogólnie rozmaitość pseudoriemannowska , k -forms mogą być identyfikowane z K -wektor pola ( k -forms są k pola -covector, a pseudo-Riemanna metryki daje izomorfizm między wektorami i covectors) i na zorientowanej przestrzeni wektorowej o postaci niezdegenerowanej (izomorfizm między wektorami i kowektorami) występuje izomorfizm między k -wektorami i ( n − k ) -wektorami; w szczególności na (przestrzeni stycznej) zorientowanej rozmaitości pseudo-Riemanna. Tak więc na zorientowanej rozmaitości pseudo-Riemanna można wymieniać k -formy, k -pola wektorowe, ( n − k ) -formy i ( n − k ) -pola wektorowe; jest to znane jako dualizm Hodge'a . Konkretnie, na R ³ jest to podane przez:

• 1-formy i 1-wektorowe pola: 1-forma a _x dx + a _y dy + a _z dz odpowiada polu wektorowemu ( a _x , a _y , a _z ) .
• 1-formy i 2-formy: zastępujemy dx liczbą dualną dy ∧ dz (tzn. pomiń dx ) i podobnie, dbając o orientację: dy odpowiada dz ∧ dx = − dx ∧ dz , a dz odpowiada dx ∧ dy . W ten sposób tworzą A _x dx + _y dy + _z dz odpowiada "podwójnej formie" a _Z dx ∧ dy + _r ms ∧ dx + _x DY ∧ ms .

W ten sposób identyfikowanie form 0 i form 3 z polami skalarnymi oraz form 1 i 2 z polami wektorowymi:

• grad przyjmuje pole skalarne (0-forma) do pola wektorowego (1-forma);
• curl zamienia pole wektorowe (w postaci 1) na pole pseudowektorowe (w postaci 2);
• div przyjmuje pole pseudowektorowe (w dwóch postaciach) do pola pseudoskalarnego (w trzech postaciach)

Z drugiej strony fakt, że d ² = 0 odpowiada tożsamościom

${\ Displaystyle \ nabla \ razy (\ nabla f) = 0}$

dla dowolnego pola skalarnego f i

${\ Displaystyle \ nabla \ cdot (\ nabla \ razy \ mathbf {v}) = 0}$

dla dowolnego pola wektorowego v .

Grad i div uogólniają na wszystkie zorientowane pseudo-Riemannowskie rozmaitości, z tą samą interpretacją geometryczną, ponieważ przestrzenie 0-form i n- form w każdym punkcie są zawsze jednowymiarowe i można je utożsamiać z polami skalarnymi, podczas gdy przestrzenie o 1 -formy i ( n − 1) -formy są zawsze n -wymiarowe włóknowe i można je utożsamiać z polami wektorowymi.

Zwijanie nie uogólnia w ten sposób do 4 lub więcej wymiarów (lub do 2 lub mniej wymiarów); w 4 wymiarach wymiary są

0 → 1 → 4 → 6 → 4 → 1 → 0;

więc rotacja pola 1-wektorowego (czterowymiarowego światłowodowego) jest polem 2-wektorowym , które w każdym punkcie należy do 6-wymiarowej przestrzeni wektorowej, a więc mamy

${\ Displaystyle \ omega ^ {(2)} = \ suma _ {i <k = 1,2,3,4} a_ {i, k} \ dx_ {i} \ klin dx_ {k}}$

co daje sumę sześciu niezależnych wyrazów i nie może być utożsamiane z polem jednowektorowym. Nie można też sensownie przejść od pola 1-wektorowego do pola 2-wektorowego do pola 3-wektorowego (4 → 6 → 4), ponieważ dwukrotne wzięcie różnicy daje zero ( d ² = 0 ). Tak więc nie ma funkcji zwijania od pól wektorowych do pól wektorowych w innych wymiarach powstających w ten sposób.

Można jednak ogólnie zdefiniować rotację pola wektorowego jako pole dwuwektorowe, jak opisano poniżej.

Zwijać geometrycznie

2 wektory odpowiadają mocy zewnętrznej Λ ² V ; w obecności iloczynu skalarnego, we współrzędnych są to macierze skośno-symetryczne, które są geometrycznie uważane za specjalną ortogonalną algebra Liego ( V ) nieskończenie małych obrotów. To ma (${\displaystyle {\mathfrak {tak}}}$ⁿ
₂) = 1/2n ( n − 1) wymiarów i pozwala interpretować różniczkę pola jednowektorowego jako jego nieskończenie małe obroty. Tylko w 3 wymiarach (lub trywialnie w 0 wymiarach) n =1/2n ( n − 1) , co jest najbardziej eleganckim i powszechnym przypadkiem. W 2 wymiarach rotacja pola wektorowego nie jest polem wektorowym, ale funkcją, ponieważ dwuwymiarowe obroty są podane przez kąt (skalar – orientacja jest wymagana, aby wybrać, czy obroty zgodnie z ruchem wskazówek zegara, czy przeciwnie do ruchu wskazówek zegara są dodatnie); to nie jest div, ale jest do niego prostopadły. W 3 wymiarach rotacja pola wektorowego jest polem wektorowym, co jest znane (w wymiarach 1 i 0 rotacja pola wektorowego wynosi 0, ponieważ nie ma nietrywialnych dwuwektorów), podczas gdy w 4 wymiarach rotacja pola wektorowego pole wektorowe jest, geometrycznie, w każdym punkcie elementem 6-wymiarowej algebry Liego. ${\displaystyle {\mathfrak {tak}}(4)}$

Wir 3-wymiarowego pola wektorowego, które zależy tylko od 2 współrzędnych (powiedzmy x i y ) jest po prostu pionowym polem wektorowym (w kierunku z ), którego wielkość jest rotacją 2-wymiarowego pola wektorowego, jak w przykładach na tej stronie.

Uwzględnienie rotacji jako pola 2-wektorowego (antysymetryczny 2-tensor) zostało wykorzystane do uogólnienia rachunku wektorowego i powiązanej fizyki do wyższych wymiarów.

Odwrotność

W przypadku, gdy rozbieżność pola wektorowego V wynosi zero, istnieje pole wektorowe W takie, że V = curl( W ) . Dlatego pole magnetyczne , charakteryzujące się zerową rozbieżnością, można wyrazić jako rotację wektora potencjału magnetycznego .

Jeśli W jest polem wektorowym z curl( W ) = V , to dodanie dowolnego pola wektorowego gradientu grad(  f  ) do W da w wyniku kolejne pole wektorowe W + grad(  f  ) takie, że curl( W + grad(  f  )) = V również. Można to podsumować stwierdzeniem, że odwrotny zwijanie trójwymiarowego pola wektorowego można uzyskać aż do nieznanego pola wirowania z prawem Biota-Savarta .

Zobacz też

Część serii artykułów o
Rachunek różniczkowy
Twierdzenie podstawowe integralna reguła Leibniza Granice funkcji Ciągłość Twierdzenie o wartości średniej Twierdzenie Rolle'a
Mechanizm różnicowy Definicje Pochodna  ( uogólnienia ) Mechanizm różnicowy nieskończenie mały funkcji całkowity Koncepcje Notacja różniczkowa Druga pochodna Niejawne zróżnicowanie Różnicowanie logarytmiczne Powiązane stawki Twierdzenie Taylora Zasady i tożsamości Suma Produkt Łańcuch Moc Iloraz Zasada L'Hôpital Odwrotność Generał Leibniz Formuła Faà di Bruno Reynoldsa
Całka Listy całek Transformacja całkowa Definicje Pochodna pierwotna Całka  ( niewłaściwa ) Całka Riemanna Integracja Lebesgue'a Integracja konturu Całka funkcji odwrotnych Integracja przez Części Dyski Cylindryczne muszle Podstawienie  ( trygonometryczne , Weierstrassa , Eulera ) Wzór Eulera Frakcje częściowe Zmiana kolejności Formuły redukcyjne Różniczkowanie pod znakiem całkowym Algorytm Richa
Seria Geometryczny  ( arytmetyczno-geometryczny ) Harmoniczny Zmienny Moc Dwumianowy Taylor Testy konwergencji Limit sumy (test terminowy) Stosunek Źródło Całka Bezpośrednie porównanie Porównanie limitów Seria naprzemienna Kondensacja Cauchy'ego Dirichleta Abel
Wektor Gradient Rozbieżność Kędzior Laplace'a Kierunkowa pochodna Tożsamości Twierdzenia Gradient Warzywa Stokesa Rozbieżność uogólniony Stokes
Wiele zmiennych Formalizmy Matryca Napinacz Zewnętrzny Geometryczny Definicje Częściowa pochodna Wielokrotna całka Całka liniowa Całka powierzchniowa Całka objętości Jakobian heski
Specjalistyczne Frakcyjny Maliavin Stochastyczny Wariacje
Różnorodny Wstępny rachunek różniczkowy Historia Słowniczek Lista tematów Pszczoła integracyjna Analiza
v T mi

• Rozkład Helmholtza
• Del we współrzędnych cylindrycznych i sferycznych
• Wirowość

Bibliografia

Dalsza lektura

• Korn, Granino Arthur i Theresa M. Korn (styczeń 2000). Podręcznik matematyczny dla naukowców i inżynierów: Definicje, twierdzenia i formuły odniesienia i przeglądu . Nowy Jork: Dover Publikacje. s. 157–160. Numer ISBN 0-486-41147-8.
• Schey, HM (1997). Div, Grad, Curl i wszystko inne: Nieformalny tekst na rachunku wektorowym . Nowy Jork: Norton. Numer ISBN 0-393-96997-5.

Zewnętrzne linki

• "Curl" , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• „Rachunek wektorowy: Zrozumienie krążenia i Curl – BetterExplained” . lepiejwyjaśnione.com . Źródło 2020-11-09 .
• „Rozbieżność i Curl: Język równań Maxwella, przepływu płynów i więcej” . 21 czerwca 2018 r. – przez YouTube .