Produkt krzyżowy - Cross product

W matematyce The produkt krzyż lub produkt wektor (czasami kierowane produkt obszar , aby podkreślić jego geometryczne znaczenie) jest binarny działanie na dwóch wektorów w przestrzeni trójwymiarowej , oraz jest oznaczona symbolem . Mając dwa liniowo niezależne wektory a i b , iloczyn poprzeczny a × b (czytaj „krzyżyk b”) jest wektorem prostopadłym do obu a i b , a zatem normalnym do płaszczyzny, która je zawiera. Ma wiele zastosowań w matematyce, fizyce , inżynierii i programowaniu komputerowym . Nie należy go mylić z iloczynem skalarnym (iloczynem rzutowania). ${\ Displaystyle \ mathbb {R} ^ {3}}$${\displaystyle \times}$

Jeśli dwa wektory w tym samym kierunku lub mają dokładnie w kierunku przeciwnym względem siebie (to znaczy, są nie liniowo niezależne), lub jeden z nich ma długość zerową, a następnie ich przekrój wynosi zero. Bardziej ogólnie, wielkość iloczynu równa się powierzchni równoległoboku z wektorami boków; w szczególności iloczyn dwóch prostopadłych wektorów jest iloczynem ich długości.

Produkt krzyżowy jest antyprzemienny (czyli a × b = − b × a ) i jest rozdzielczy względem dodawania (czyli a × ( b + c ) = a × b + a × c ). Przestrzeń wraz z iloczynem krzyżowym jest algebrą nad liczbami rzeczywistymi , która nie jest ani przemienna ani asocjacyjna , ale jest algebrą Liego, w której iloczynem krzyżowym jest nawias Liego . ${\ Displaystyle \ mathbb {R} ^ {3}}$

Jak iloczynu skalarnego, to zależy od metryki z przestrzeni euklidesowej , ale w odróżnieniu od iloczynu skalarnego, to również zależy od wyboru orientacji lub „ bezstronności ”. Produkt można uogólniać na różne sposoby; może być niezależna od orientacji zmieniając wynik pseudowektor lub od zewnątrz wektory mogą być stosowane w dowolnych wymiarach z bivector lub 2-formy związku. Ponadto, używając orientacji i struktury metrycznej, tak jak w przypadku tradycyjnego trójwymiarowego produktu krzyżowego, można w n wymiarach wziąć iloczyn n − 1 wektorów, aby otrzymać wektor prostopadły do ​​wszystkich z nich. Ale jeśli iloczyn jest ograniczony do nietrywialnych iloczynów binarnych z wynikami wektorowymi, istnieje tylko w trzech i siedmiu wymiarach . (Patrz § Uogólnienia poniżej, dla innych wymiarów.)

Definicja

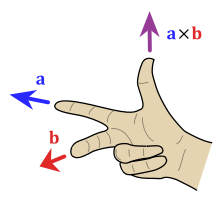
Iloczyn poprzeczny dwóch wektorów a i b jest zdefiniowany tylko w przestrzeni trójwymiarowej i jest oznaczony przez a × b . W fizyce i matematyce stosowanej notacja klina a ∧ b jest często używana (w połączeniu z nazwą iloczyn wektorowy ), chociaż w czystej matematyce taki zapis jest zwykle zarezerwowany tylko dla iloczynu zewnętrznego, abstrakcji iloczynu wektorowego do n wymiarów.

Iloczyn poprzeczny a × b jest zdefiniowany jako wektor c, który jest prostopadły (prostokątny) zarówno do a , jak i b , z kierunkiem określonym przez regułę prawej ręki i wielkością równą powierzchni równoległoboku, którą obejmują wektory.

Iloczyn krzyżowy jest określony wzorem

${\ Displaystyle \ mathbf {a} \ razy \ mathbf {b} = \ po lewej \ | \ mathbf {a} \ po prawej \ | \ po lewej \ | \ mathbf {b} \ po prawej \ | \ grzech (\ teta) \ \ \ matematyka {n.}$

gdzie:

• θ to kąt między a i b w płaszczyźnie je zawierającej (stąd wynosi od 0° do 180°)
• ‖ ‖ I ‖ b ‖ są wielkości wektorów i B
• i n jest urządzenie wektor prostopadły do płaszczyzny zawierającej i B w kierunku określonym przez regułę prawej stronie (na rysunku).

Jeśli wektory A i B są równolegle (to jest kąt θ między nimi jest równe 0 ° lub 180 °), w powyższym wzorze, iloczynu i b jest wektor zerowy 0 .

Kierunek

Zgodnie z konwencją kierunek wektora n określa reguła prawej ręki, w której palec wskazujący prawej ręki wskazuje się po prostu w kierunku a, a środkowy w kierunku b . Wtedy wektor n wychodzi z kciuka (patrz rysunek obok). Użycie tej reguły oznacza, że ​​iloczyn krzyżowy jest antyprzemienny ; czyli b × a = −( a × b ) . Wskazując najpierw palec wskazujący w kierunku b , a następnie wskazując palec środkowy w kierunku a , kciuk zostanie przesunięty w przeciwnym kierunku, odwracając znak wektora iloczynu.

Ponieważ operator iloczynu krzyżowego zależy od orientacji przestrzeni (jak to zostało wyraźnie określone w powyższej definicji), iloczyn krzyżowy dwóch wektorów nie jest „prawdziwym” wektorem, ale pseudowektorem . Więcej szczegółów znajdziesz w § Praworęczność .

Nazwy

W 1881 roku, Jozyjasz Willard Gibbsa , i niezależnie Oliver Heaviside wprowadzony zarówno iloczyn skalarny i produkt przekrój pomocą kropki ( . B ), a „X” ( a x b ), odpowiednio, ich oznaczenia.

W 1877 roku, aby podkreślić fakt, że wynikiem iloczynu skalarnego jest skalar, podczas gdy wynikiem iloczynu krzyżowego jest wektor , William Kingdon Clifford ukuł alternatywne nazwy iloczynu skalarnego i iloczynu wektorowego dla tych dwóch operacji. Te alternatywne nazwy są nadal szeroko stosowane w literaturze.

Zarówno oznaczenie przekroju ( x b ) i nazwę iloczyn była inspirowana prawdopodobnie z faktu, że każdy skalarne składnik o a x b jest obliczany przez mnożenie nie-odpowiadające składniki i b . I odwrotnie, iloczyn skalarny a ⋅ b obejmuje mnożenie odpowiednich składowych a i b . Jak wyjaśniono poniżej , iloczyn krzyżowy może być wyrażony w postaci wyznacznika specjalnej macierzy 3×3 . Zgodnie z regułą Sarrusa polega to na mnożeniu elementów macierzy identyfikowanych przez skrzyżowane przekątne.

Przetwarzanie danych

Notacja współrzędnych

W standardowej podstawy wektory i , j oraz k spełniać następujące równości w prawej ręce układu współrzędnych :

${\ Displaystyle {\ zacząć {wyrównany} {2} \ mathbf {\ kolor {niebieski} {i}} i \ razy \ mathbf {\ kolor {czerwony} {j}} & & = \ mathbf {\ kolor {zielony} k}} \\\mathbf {\color {red}{j}} &\times \mathbf {\color {green}{k}} &&=\mathbf {\color {blue}{i}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {blue}{i}} &&=\mathbf {\color {red}{j}} \end{alignedat}}}$

co implikuje, przez antyprzemienność produktu krzyżowego, że

${\ Displaystyle {\ zacząć {wyrównany} {2} \ mathbf {\ kolor {czerwony} {j}} i \ razy \ mathbf {\ kolor {niebieski} {i}} & & = - \ mathbf {\ kolor {zielony} {k}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {red}{j}} &&=-\mathbf {\color {blue}{i}} \\ \mathbf {\color {blue}{i}} &\times \mathbf {\color {green}{k}} &&=-\mathbf {\color {red}{j}} \end{alignedat}}}$

Antyprzemienność iloczynu krzyżowego (i oczywisty brak liniowej niezależności) również implikuje, że

${\ Displaystyle \ mathbf {\ kolor {niebieski}{i}} \ razy \ mathbf {\ kolor {niebieski} {i}} = \ mathbf {\ kolor {czerwony} {j}} \ razy \ mathbf {\ kolor { czerwony}{j}} =\mathbf {\color {zielony}{k}} \times \mathbf {\color {zielony}{k}} =\mathbf {0} }$( wektor zerowy ).

Te równości, wraz z rozdzielnością i liniowością iloczynu poprzecznego (choć żadne z nich nie wynika łatwo z definicji podanej powyżej), są wystarczające do wyznaczenia iloczynu poprzecznego dowolnych dwóch wektorów a i b . Każdy wektor można zdefiniować jako sumę trzech składowych ortogonalnych równoległych do standardowych wektorów bazowych:

${\ Displaystyle {\ zacząć {wyrównany} {3} \ mathbf {a} & = a_ {1} \ mathbf {\ kolor {niebieski} {i}} i & + a_ {2} \ mathbf {\ kolor {czerwony} j}} &&+a_{3}\mathbf {\color {green}{k}} \\\mathbf {b} &=b_{1}\mathbf {\color {blue}{i}} &&+b_{ 2}\mathbf {\color {red}{j}} &&+b_{3}\mathbf {\color {green}{k}} \end{alignedat}}}$

Ich iloczyn krzyżowy a × b można rozszerzyć za pomocą rozdzielności:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a} \ razy \ mathbf {b} = {} i (a_ {1} \ mathbf {\ kolor {niebieski} {i}} + a_ {2} \ mathbf { \color {czerwony}{j}} +a_{3}\mathbf {\color {zielony}{k}} )\times (b_{1}\mathbf {\color {niebieski}{i}} +b_{2 }\mathbf {\color {czerwony}{j}} +b_{3}\mathbf {\color {zielony}{k}} )\\={}&a_{1}b_{1}(\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} )+a_{1}b_{2}(\mathbf {\color {blue}{i}} \times \mathbf {\ color {red}{j}} )+a_{1}b_{3}(\mathbf {\color {blue}{i}} \times \mathbf {\color {green}{k}} )+{}\ \&a_{2}b_{1}(\mathbf {\color {czerwony}{j}} \times \mathbf {\color {niebieski}{i}} )+a_{2}b_{2}(\mathbf { \color {czerwony}{j}} \times \mathbf {\color {czerwony}{j}} )+a_{2}b_{3}(\mathbf {\color {czerwony}{j}} \times \mathbf {\color {green}{k}} )+{}\\&a_{3}b_{1}(\mathbf {\color {green}{k}} \times \mathbf {\color {blue}{i} } )+a_{3}b_{2}(\mathbf {\color {zielony}{k}} \times \mathbf {\color {czerwony}{j}} )+a_{3}b_{3}(\ mathbf {\color {zielony}{k}} \times \mathbf {\color {zielony}{k}} )\\\end{wyrównany}}}$

Można to zinterpretować jako rozkład a × b na sumę dziewięciu prostszych produktów krzyżowych obejmujących wektory wyrównane z i , j lub k . Każdy z tych dziewięciu produktów krzyżowych działa na dwóch wektorach, które są łatwe w obsłudze, ponieważ są do siebie równoległe lub prostopadłe. Z tej dekompozycji, posługując się wyżej wymienionymi równościami i zbierając podobne terminy, otrzymujemy:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a} \ razy \ mathbf {b} = {} i \ quad \ a_ {1} b_ {1} \ mathbf {0} + a_ {1} b_ {2} \mathbf {\color {zielony}{k}} -a_{1}b_{3}\mathbf {\color {czerwony}{j}} \\&-a_{2}b_{1}\mathbf {\color {zielony}{k}} +a_{2}b_{2}\mathbf {0} +a_{2}b_{3}\mathbf {\color {niebieski}{i}} \\&+a_{3} b_{1}\mathbf {\color {czerwony}{j}} \ -a_{3}b_{2}\mathbf {\color {niebieski}{i}} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2})\mathbf {\color {niebieski}{i}} +(a_{3}b_{1} -a_{1}b_{3})\mathbf {\color {czerwony}{j}} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {\color {zielony} {k}} \\\koniec{wyrównany}}}$

co oznacza, że ​​trzy składowe skalarne otrzymanego wektora s = s ₁ i + s ₂ j + s ₃ k = a × b są

${\displaystyle {\begin {wyrównany}s_{1}&=a_{2}b_{3}-a_{3}b_{2}\\s_{2}&=a_{3}b_{1}-a_ {1}b_{3}\\s_{3}&=a_{1}b_{2}-a_{2}b_{1}\end{aligned}}}$

Używając wektorów kolumnowych , możemy przedstawić ten sam wynik w następujący sposób:

${\displaystyle {\zaczynać{pmatrix}s_{1}\\s_{2}\\s_{3}\koniec{pmatrix}}={\zaczynać{pmatrix}a_{2}b_{3}-a_{3 }b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{pmatrix}}}$

Notacja macierzowa

Iloczyn krzyżowy można również wyrazić jako wyznacznik formalny :

${\ Displaystyle \ mathbf {a \ razy b} = {\ zacząć {vmatrix} \ mathbf {i} & \ mathbf {j} & \ mathbf {k} \ \ a_ {1} i a_ {2} i a_ {3}\ \b_{1}&b_{2}&b_{3}\\\end{vmatrix}}}$

Ten wyznacznik można obliczyć za pomocą reguły Sarrusa lub rozwinięcia kofaktora . Korzystając z reguły Sarrusa, rozszerza się do

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a \ razy b} & = (a_ {2} b_ {3} \ mathbf {i} + a_ {3} b_ {1} \ mathbf {j} + a_ { 1}b_{2}\mathbf {k} )-(a_{3}b_{2}\mathbf {i} +a_{1}b_{3}\mathbf {j} +a_{2}b_{1} \mathbf {k} )\\&=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_ {3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} .\end{wyrównany}}}$

Używając ekspansji kofaktora wzdłuż pierwszego rzędu, rozszerza się do

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a \ razy b} & = {\ zacząć {vmatrix} a_ {2} i a_ {3} \ \ b_ {2} i b_ {3} \ koniec {vmatrix}} \ mathbf {i} -{\begin{vmatrix}a_{1}&a_{3}\\b_{1}&b_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}a_{1 }&a_{2}\\b_{1}&b_{2}\end{vmatrix}}\mathbf {k} \\&=(a_{2}b_{3}-a_{3}b_{2})\ mathbf {i} -(a_{1}b_{3}-a_{3}b_{1})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\ mathbf {k} ,\koniec{wyrównany}}}$

co bezpośrednio daje składowe otrzymanego wektora.

Korzystanie z tensorów Levi-Civita

• W dowolnej podstawie iloczyn krzyżowy jest określony wzorem tensoryjnym, gdzie jest kowariantnym tensorem Levi-Civita (zwracamy uwagę na położenie indeksów). Odpowiada to podanej tutaj wewnętrznej formule .${\displaystyle a\razy b}$${\ Displaystyle E_ {ijk} a ^ {i} b ^ {j}}$${\ Displaystyle E_ {ijk}}$
• W bazie ortonormalnej mającej taką samą orientację jak przestrzeń , dane jest wzorem pseudotensorialnym, gdzie jest symbolem Levi-Civita (który jest pseudotensorem). To wzór używany w codziennej fizyce, ale działa tylko w tym szczególnym przypadku podstawy.${\displaystyle a\razy b}$${\ Displaystyle \ varepsilon _ {ijk} a ^ {i} b ^ {j}}$${\ Displaystyle \ varepsilon _ {ijk}}$
• W dowolnej bazie ortonormalnej jest podany przez wzór pseudotensoryczny, w którym wskazuje, czy baza ma taką samą orientację jak przestrzeń, czy nie.${\displaystyle a\razy b}$${\ Displaystyle (-1) ^ {B} \ varepsilon _ {ijk} a ^ {i} b ^ {j}}$${\ Displaystyle (-1) ^ {B} = \ pm 1}$

Ten drugi wzór pozwala uniknąć konieczności zmiany orientacji przestrzeni, gdy odwracamy bazę ortonormalną.

Nieruchomości

Znaczenie geometryczne

Wielkość produktu poprzeczny może być interpretowany jako pozytywne powierzchni z równoległoboku o i B w bokach (patrz Figura 1):

${\ Displaystyle \ lewo \ | \ mathbf {a} \ razy \ mathbf {b} \ po prawej \ | = \ po lewej \ | \ mathbf {a} \ po prawej \ | \ po lewej \ | \ mathbf {b} \ po prawej \ | |\sin \theta |.}$

W istocie, można również wyliczyć objętość V o równoległościanu posiadającego się , B i C , jak krawędzie z zastosowaniem kombinacji iloczynu i iloczynu skalarnego zwany skalarne potrójne produktu (patrz figura 2):

${\ Displaystyle \ mathbf {a} \ cdot ( \ mathbf {b} \ razy \ mathbf {c} ) = \ mathbf {b} \ cdot ( \ mathbf {c} \ razy \ mathbf {a} ) = \ mathbf { c} \cdot (\mathbf {a} \times \mathbf {b} ).}$

Ponieważ wynik iloczynu skalarnego potrójnego może być ujemny, objętość równoległościanu jest podana przez jego wartość bezwzględną. Na przykład,

${\ Displaystyle V = | \ mathbf {a} \ cdot (\ mathbf {b} \ razy \ mathbf {c}) |.}$

Ponieważ wielkość iloczynu krzyżowego jest równa sinusowi kąta między jego argumentami, iloczyn krzyżowy można traktować jako miarę prostopadłości w taki sam sposób, w jaki iloczyn skalarny jest miarą równoległości . Biorąc pod uwagę dwa wektory jednostkowe , ich iloczyn poprzeczny ma wartość 1, jeśli oba są prostopadłe i wartość zero, jeśli są równoległe. Iloczyn skalarny dwóch wektorów jednostkowych zachowuje się dokładnie odwrotnie: wynosi zero, gdy wektory jednostkowe są prostopadłe i 1, gdy wektory jednostkowe są równoległe.

Wektory jednostkowe umożliwiają dwie dogodne tożsamości: iloczyn skalarny dwóch wektorów jednostkowych daje cosinus (który może być dodatni lub ujemny) kąta między dwoma wektorami jednostkowymi. Wartość iloczynu krzyżowego dwóch wektorów jednostkowych daje sinus (który zawsze będzie dodatni).

Własności algebraiczne

Jeśli iloczynem krzyżowym dwóch wektorów jest wektor zerowy (to znaczy a × b = 0 ), wtedy jedno lub oba wejścia są wektorem zerowym ( a = 0 lub b = 0 ) lub są one równoległe lub antyrównoległy ( a ∥ b ) tak, że sinus kąta między nimi wynosi zero ( θ = 0° lub θ = 180° i sin  θ = 0 ).

Iloczynem własnym wektora jest wektor zerowy:

${\ Displaystyle \ mathbf {a} \ razy \ mathbf {a} = \ mathbf {0}.}$

Produkt krzyżowy jest antyprzemienny ,

${\ Displaystyle \ mathbf {a} \ razy \ mathbf {b} =-(\ mathbf {b} \ razy \ mathbf {a}),}$

rozdzielczy nad dodawaniem,

${\ Displaystyle \ mathbf {a} \ razy (\ mathbf {b} + \ mathbf {c}) = (\ mathbf {a} \ razy \ mathbf {b}) + (\ mathbf {a} \ razy \ mathbf { C} ),}$

i kompatybilny z mnożeniem przez skalar, dzięki czemu

${\ Displaystyle (r\, \ mathbf {a} ) \ razy \ mathbf {b} = \ mathbf {a} \ razy (r \, \ mathbf {b} ) = r \, (\ mathbf {a} \ razy \mathbf {b} ).}$

Nie jest skojarzeniowa , ale spełnia tożsamość Jacobiego :

${\ Displaystyle \ mathbf {a} \ razy (\ mathbf {b} \ razy \ mathbf {c}) + \ mathbf {b} \ razy (\ mathbf {c} \ razy \ mathbf {a} ) + \ mathbf { c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0} .}$

Dystrybucja, liniowość i tożsamość Jacobiego pokazują, że przestrzeń wektorowa R ³ wraz z dodawaniem wektorów i iloczynem krzyżowym tworzy algebrę Liego , algebrę Liego rzeczywistej grupy ortogonalnej w 3 wymiarach, SO(3) . Produkt krzyżowy nie jest zgodny z prawem anulowania ; to znaczy, a × b = a × c z a ≠ 0 nie implikuje b = c , ale tylko to:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {0} & = (\ mathbf {a} \ razy \ mathbf {b}) - (\ mathbf {a} \ razy \ mathbf {c}) \ \ & = \ mathbf {a} \times (\mathbf {b} -\mathbf {c} ).\\\end{wyrównany}}}$

Może to być przypadek, w którym b oraz c zrezygnować, a dodatkowo, gdy i b - C są równoległe; oznacza to, że są powiązane współczynnikiem skali t , co prowadzi do:

${\ Displaystyle \ mathbf {c} = \ mathbf {b} + t \, \ mathbf {a},}$

dla niektórych skalarnych t .

Jeśli oprócz x b = x C i ≠ 0 , jak wyżej, to jest tak, że ⋅ b = ⋅ C , a następnie

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a} \ razy (\ mathbf {b} - \ mathbf {c} ) i = \ mathbf {0} \ \ \ mathbf {a} \ cdot (\ mathbf {b } -\mathbf {c} )&=0,\end{wyrównany}}}$

Ponieważ b − c nie może być jednocześnie równoległe (aby iloczyn poprzeczny wynosił 0 ) i prostopadły (aby iloczyn skalarny miał wartość 0) do a , musi być tak, że b i c anulują: b = c .

Z definicji geometrycznej iloczyn poprzeczny jest niezmienny przy odpowiednich obrotach wokół osi określonej przez a × b . We wzorach:

${\ Displaystyle (R \ mathbf {a} ) \ razy (R \ mathbf {b} ) = R (\ mathbf {a} \ razy \ mathbf {b})}$, gdzie jest macierzą rotacji z .${\ Displaystyle R}$${\ Displaystyle \ det (R) = 1}$

Bardziej ogólnie, produkt krzyżowy zachowuje następującą tożsamość w przekształceniach macierzowych :

${\ Displaystyle (M \ mathbf {a} ) \ razy (M \ mathbf {b} ) = (\ DET M) \ lewo (M ^ {-1} \ prawej) ^ {\ operatorname {T}} (\ mathbf {a} \times \mathbf {b} )=\operatorname {cof} M(\mathbf {a} \times \mathbf {b} )}$

w którym jest 3-o-3 matrycy i jest transpozycją z odwrotności i macierz kofaktora. Łatwo zauważyć, jak ten wzór redukuje się do poprzedniego, jeśli jest macierzą rotacji. ${\ Displaystyle M}$${\ Displaystyle \ lewo (M ^ {-1} \ po prawej) ^ {\ operator {T}}}$${\displaystyle \operatorname {cof}}$${\ Displaystyle M}$

Przekrój dwóch wektorów leży w przestrzeni zerowej w 2 x 3 matryca z wektorów jak rzędach

${\ Displaystyle \ mathbf {a} \ razy \ mathbf {b} \ w NS \ po lewej ({\ zacznij {bmatrycy} \ mathbf {a} \\ \ mathbf {b} \ koniec {bmacierzy}} \ prawej).}$

W przypadku sumy dwóch produktów krzyżowych obowiązuje następująca tożsamość:

${\ Displaystyle \ mathbf {a} \ razy \ mathbf {b} + \ mathbf {c} \ razy \ mathbf {d} = (\ mathbf {a} - \ mathbf {c} ) \ razy (\ mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b} .}$

Różnicowanie

Zasada iloczynowa rachunku różniczkowego ma zastosowanie do każdej operacji dwuliniowej, a zatem również do iloczynu krzyżowego:

${\ Displaystyle {\ Frac {d} {dt}} (\ mathbf {a} \ razy \ mathbf {b} ) = {\ Frac {d \ mathbf {a}} {dt}} \ razy \ mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}},}$

gdzie a i b są wektorami zależnymi od rzeczywistej zmiennej t .

Potrójna ekspansja produktu

Produkt krzyżowy jest używany w obu formach iloczynu potrójnego. Skalarne potrójną trzech wektorów jest zdefiniowany jako

${\ Displaystyle \ mathbf {a} \ cdot (\ mathbf {b} \ razy \ mathbf {c}}),}$

Jest to podpisana objętość równoległościanu z krawędziami a , b i c i jako takie wektory mogą być używane w dowolnej kolejności, która jest parzystą permutacją powyższej kolejności. Następujące zatem są równe:

${\ Displaystyle \ mathbf {a} \ cdot ( \ mathbf {b} \ razy \ mathbf {c} ) = \ mathbf {b} \ cdot ( \ mathbf {c} \ razy \ mathbf {a} ) = \ mathbf { c} \cdot (\mathbf {a} \times \mathbf {b} ),}$

Wektor potrójną jest iloczynem wektora z wynikiem innego iloczynu i jest związane z iloczynu skalarnego według następującego wzoru

${\ Displaystyle \ mathbf {a} \ razy (\ mathbf {b} \ razy \ mathbf {c}) = \ mathbf {b} (\ mathbf {a} \ cdot \ mathbf {c}) - \ mathbf {c} (\mathbf {a} \cdot \mathbf {b} ).}$

Mnemonic „BAC minus CAB” jest używany do zapamiętania kolejności wektorów w członie po prawej stronie. Ten wzór jest używany w fizyce w celu uproszczenia obliczeń wektorowych. Szczególnym przypadkiem dotyczącym gradientów i przydatnym w rachunku wektorowym jest

${\ Displaystyle {\ zacząć {wyrównany} \ nabla \ razy (\ nabla \ razy \ mathbf {f}) i = \ nabla (\ nabla \ cdot \ mathbf {f}) - (\ nabla \ cdot \ nabla) \ mathbf {f} \\&=\nabla (\nabla \cdot \mathbf {f} )-\nabla ^{2}\mathbf {f} ,\\\end{wyrównany}}}$

gdzie ∇ ² jest wektorem operatora Laplace'a .

Inne tożsamości wiążą iloczyn krzyżowy z potrójnym iloczynem skalarnym:

${\ Displaystyle {\ zacząć {wyrównany} (\ mathbf {a} \ razy \ mathbf {b}) \ razy (\ mathbf {a} \ razy \ mathbf {c}) & = (\ mathbf {a} \ cdot ( \mathbf {b} \times \mathbf {c} ))\mathbf {a} \\(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )&=\mathbf {b} ^{\mathrm {T} }\left(\left(\mathbf {c} ^{\mathrm {T} }\mathbf {a} \right)I-\mathbf {c} \mathbf {a} ^{\mathrm {T} }\right)\mathbf {d} \\&=(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf { d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )\end{wyrównany}}}$

gdzie I jest macierzą tożsamości.

Alternatywna formuła

Iloczyn krzyżowy i iloczyn skalarny są powiązane przez:

${\ Displaystyle \ lewo \ | \ mathbf {a} \ razy \ mathbf {b} \ po prawej \ | ^ {2} = \ po lewej \ | \ mathbf {a} \ po prawej \ | ^ {2} \ po lewej \ | \ mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.}$

Po prawej stronie jest wyznacznikiem Gram z i b , kwadratowy obszaru równoległoboku określonym przez wektory. Ten warunek określa wielkość iloczynu krzyżowego. Mianowicie, ponieważ iloczyn skalarny jest zdefiniowany w kategoriach kąta θ między dwoma wektorami jako:

${\ Displaystyle \ mathbf {a \ cdot b} = \ po lewej \ | \ mathbf {a} \ po prawej \ | \ po lewej \ | \ mathbf {b} \ po prawej \ | \ cos \ teta,}$

powyższy związek można przepisać w następujący sposób:

${\ Displaystyle \ po lewej \ | \ mathbf {a \ razy b} \ po prawej \ | ^ {2} = \ po lewej \ | \ mathbf {a} \ po prawej \ | ^ {2} \ po lewej \ | \ mathbf {b} \right\|^{2}\left(1-\cos ^{2}\theta \right).}$

Odwołując się do pitagorejskiej tożsamości trygonometrycznej otrzymujemy:

${\ Displaystyle \ lewo \ | \ mathbf {a} \ razy \ mathbf {b} \ po prawej \ | = \ po lewej \ | \ mathbf {a} \ po prawej \ | \ po lewej \ | \ mathbf {b} \ po prawej \ | \left|\sin \theta \right|,}$

który jest wielkość produktu przekroju wyrażone w θ , równej powierzchni równoległoboku określonej przez i B (patrz definicja powyżej).

Połączenie tego wymogu i tę właściwość, że produkt jest prostopadła do przekroju jego składników a i b umożliwia alternatywną definicji produktu poprzecznym.

Tożsamość Lagrange'a

Relacja:

${\ Displaystyle \ lewo \ | \ mathbf {a} \ razy \ mathbf {b} \ prawo \ | ^ {2} \ równoważnik \ det {\ zacząć {bmatrix} \ mathbf {a} \ cdot \ mathbf {a} i \mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{bmatrix}}\equiv \ left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{ 2}.}$

można porównać z inną relacją dotyczącą prawej strony, a mianowicie tożsamością Lagrange'a wyrażoną jako:

${\ Displaystyle \ suma _ {1 \ leq i <j \ leq n} \ lewo (a_ {i} b_ {j}-a_ {j} b_ {i} \ po prawej) ^ {2} \ równoważnik \ po lewej \ | \mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a\cdot b} )^{2}\ ,}$

gdzie i b mogą być N -wymiarowych wektorów. Pokazuje to również, że postać objętości Riemanna dla powierzchni jest dokładnie elementem powierzchni z rachunku wektorowego. W przypadku, gdy n = 3 , połączenie tych dwóch równań daje wyrażenie na wielkość iloczynu krzyżowego w kategoriach jego składowych:

${\ Displaystyle {\ zacząć {wyrównane} i \ lewo \ | \ mathbf {a} \ razy \ mathbf {b} \ prawo \ | ^ {2} \ równoważne \ suma _ {1 \ równoważnik i<j \ równoważnik 3} \left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\\\equiv {}&\left(a_{1}b_{2}-b_{1} a_{2}\right)^{2}+\left(a_{2}b_{3}-a_{3}b_{2}\right)^{2}+\left(a_{3}b_{1} }-a_{1}b_{3}\right)^{2}\ .\end{aligned}}}$

Ten sam wynik można znaleźć bezpośrednio przy użyciu składników produktu krzyżowego znalezionego z:

${\ Displaystyle \ mathbf {a} \ razy \ mathbf {b} \ równoważny \ det {\ zacząć {bmatrix} {\ kapelusz {\ mathbf {i}}} i {\ kapelusz {\ mathbf {j}}} i { \hat {\mathbf {k} }}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{bmatrix}}.}$

W R ³ równanie Lagrange'a jest szczególnym przypadkiem multiplikatywności | vw | = | v || w | normy w algebrze kwaternionów .

Jest to szczególny przypadek innej formuły, zwanej również czasami tożsamością Lagrange'a, która jest trójwymiarowym przypadkiem tożsamości Bineta-Cauchy'ego :

${\ Displaystyle ( \ mathbf {a} \ razy \ mathbf {b} ) \ cdot ( \ mathbf {c} \ razy \ mathbf {d} ) \ równoważne ( \ mathbf {a} \ cdot \ mathbf {c} ) ( \mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} ).}$

Jeśli a = c i b = d to upraszcza się do powyższego wzoru.

Nieskończone generatory obrotów

Iloczyn krzyżowy dogodnie opisuje nieskończenie małe generatory obrotów w R ³ . W szczególności, jeśli n jest wektorem jednostkowym w R ³ i R ( φ ,  n ) oznacza obrót wokół osi przez początek określony przez n , o kącie φ (mierzonym w radianach, w kierunku przeciwnym do ruchu wskazówek zegara, patrząc od wierzchołka n ), to

${\ Displaystyle \ lewo. {d \ nad d \ phi} \ prawo | _ {\ phi = 0} R (\ phi {\ pogrubienie {n}}} {\ pogrubienie {x}} = {\ pogrubienie {n }}\times {\boldsymbol {x}}}$

dla każdego wektora x w R ³ . Iloczyn krzyżowy z n opisuje zatem nieskończenie mały generator obrotów wokół n . Te nieskończenie małe generatory tworzą algebrę Liego so (3) grupy obrotowej SO(3) , i otrzymujemy wynik, że algebra Liego R ³ z iloczynem krzyżowym jest izomorficzna z algebrą Liego so (3).

Alternatywne sposoby obliczania

Konwersja do mnożenia macierzy

Iloczyn krzyżowy wektora można również wyrazić jako iloczyn macierzy skośno-symetrycznej i wektora:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a} \ razy \ mathbf {b} = [\ mathbf {a} ] _ {\ razy} \ mathbf {b} & = {\ zacząć {bmatrix} \ 0& \!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1} &\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}\\\mathbf {a} \times \mathbf { b} ={[\mathbf {b} ]_{\times }}^{\mathrm {\!\!T} }\mathbf {a} &={\begin{bmatrix}\,0&\,\,b_ {3}&\!-b_{2}\\-b_{3}&0&\,\,b_{1}\\\,\,b_{2}&\!-b_{1}&\,0\ end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}},\end{aligned}}}$

gdzie indeks górny ^T odnosi się do operacji transpozycji , a [ a ] _× jest zdefiniowany przez:

${\ Displaystyle [\ mathbf {a} ] _ {\ razy }{\ stackrel {\ rm {def}}{=}}{\ zacznij {bmatrix} \, \, 0 i \! -a_ {3} i \, \,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\ ,0\koniec{bmatrycy}}.}$

Kolumny [ a ] _×,i macierzy skośno-symetrycznej dla wektora a można również uzyskać, obliczając iloczyn poprzeczny z wektorami jednostkowymi . To jest,

${\ Displaystyle [\ mathbf {a} ]_ {\ razy, ja} = \ mathbf {a} \ razy \ mathbf {{\ kapelusz {e}} _ {i}}, \; ja \ w \ {1, 2,3\}}$

lub

${\ Displaystyle [\ mathbf {a} ] _ {\ razy} = \ suma _ {i = 1} ^ {3} \ lewo (\ mathbf {a} \ razy \ mathbf {{\ kapelusz {e}} _ { i}} \right)\otimes \mathbf {{\hat {e}}_{i}} ,}$

gdzie jest zewnętrzny operator produktu . ${\ Displaystyle \ czasami}$

Ponadto, jeśli samo a jest wyrażone jako iloczyn krzyżowy:

${\ Displaystyle \ mathbf {a} = \ mathbf {c} \ razy \ mathbf {d}}$

następnie

${\ Displaystyle [\ mathbf {a} ] _ {\ razy} = \ mathbf {d} \ mathbf {c} ^ {\ mathbf {T}} - \ mathbf {c} \ mathbf {d} ^ {\ mathrm { T} }.}$

Dowód przez podstawienie

Ocena produktu krzyżowego daje ${\ Displaystyle \ mathbf {a} = \ mathbf {c} \ razy \ mathbf {d} = {\ zacząć {pmatrix} c_ {2}d_ {3}-c_ {3}d_ {2} \ \ c_ {3 }d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}\end{pmatrix}}}$ Stąd lewa strona równa się ${\ Displaystyle [\ mathbf {a} ] _ {\ razy} = {\ zacząć {bmatrix} 0 i c_ {2}d_ {1}-c_ {1} d_ {2} i c_ {3}d_ {1}-c_ { 1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{ 3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}}$ Teraz po prawej stronie ${\ Displaystyle \ mathbf {c} \ mathbf {d} ^ {\ operatorname {T}} = {\ zacząć {bmatrix} c_ {1} d_ {1} i c_ {1} d_ {2} i c_ {1} d_ { 3}\\c_{2}d_{1}&c_{2}d_{2}&c_{2}d_{3}\\c_{3}d_{1}&c_{3}d_{2}&c_{3} d_{3}\koniec{bmatrycy}}}$ A jego transpozycja to ${\ Displaystyle \ mathbf {d} \ mathbf {c} ^ {\ operatorname {T}} = {\ zacząć {bmatrix} c_ {1} d_ {1} i c_ {2} d_ {1} i c_ {3} d_ { 1}\\c_{1}d_{2}&c_{2}d_{2}&c_{3}d_{2}\\c_{1}d_{3}&c_{2}d_{3}&c_{3} d_{3}\koniec{bmatrycy}}}$ Ocena z prawej strony daje ${\ Displaystyle \ mathbf {d} \ mathbf {c} ^ {\ operatorname {T}} - \ mathbf {c} \ mathbf {d} ^ {\ operatorname {T}} = {\ zacząć {bmatrix} 0 i c_ {2 }d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1} &0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_ {2}&0\koniec{bmatrycy}}}$ Porównanie pokazuje, że lewa strona równa się prawej stronie.

Ten wynik można uogólnić na wyższe wymiary za pomocą algebry geometrycznej . W szczególności w dowolnym wymiarze dwuwektory można utożsamiać z macierzami skośno-symetrycznymi, więc iloczyn między macierzą skośno-symetryczną a wektorem jest równoważny części stopnia 1 iloczynu dwuwektora i wektora. W trzech wymiarach dwuwektory są dualne do wektorów, więc iloczyn jest równoważny iloczynowi krzyżowemu, z dwuwektorem zamiast jego wektorem dualnym. W wyższych wymiarach iloczyn nadal można obliczyć, ale dwuwektory mają więcej stopni swobody i nie są równoważne wektorom.

Ta notacja jest również często znacznie łatwiejsza do pracy, na przykład w geometrii epipolarnej .

Z ogólnych właściwości iloczynu krzyżowego wynika od razu, że

${\ Displaystyle [\ mathbf {a}] _ {\ razy} \ \ mathbf {a} = \ mathbf {0}}$   oraz   ${\ Displaystyle \ mathbf {a} ^ {\ operatorname {T}} \ [\ mathbf {a}] _ {\ razy} = \ mathbf {0}}$

a z faktu, że [ a ] _× jest skośnie symetryczne wynika, że

${\ Displaystyle \ mathbf {b} ^ {\ mathrm {T}} \ [\ mathbf {a}] _ {\ razy} \ \ mathbf {b} = 0.}$

Wspomniane powyżej potrójne rozszerzenie produktu (zasada bac-cab) można łatwo udowodnić za pomocą tego zapisu.

Jak wspomniano powyżej, algebra Liego R ³ z iloczynem krzyżowym jest izomorficzna z algebrą Liego so(3) , której elementy można utożsamiać z macierzami skośno-symetrycznymi 3×3. Odwzorowanie a → [ a ] _× zapewnia izomorfizm pomiędzy R ³ i tak(3) . Pod tą mapą iloczyn poprzeczny 3 wektorów odpowiada komutatorowi macierzy 3x3 skośno-symetrycznych.

Konwersja macierzy dla iloczynu krzyżowego z kanonicznymi wektorami bazowymi

Oznaczając w tym -tym kanonicznego wektora bazowej iloczynu generycznego wektora z jest dana przez: gdzie ${\ Displaystyle \ mathbf {e} _ {i} \ w \ mathbf {R} ^ {3 \ razy 1}}$${\displaystyle i}$${\ Displaystyle \ mathbf {v} \ w \ mathbf {R} ^ {3 \ razy 1}}$${\ Displaystyle \ mathbf {e} _ {i}}$${\ Displaystyle \ mathbf {v} \ razy \ mathbf {e} _ {i} = \ mathbf {C} _ {i} \ mathbf {v}}$ ${\ Displaystyle \ mathbf {C} _ {1} = {\ zacząć {bmatrix} 0 i 0 i 0 \ \ 0 i 0 i 1 \ \ 0 i 1 i 0 \ koniec {bmatrix}}, \ quad \ mathbf {C} _ {2} = {\ zacząć {bmatrix}0&0&-1\\0&0&0\\1&0&0\end{bmatrix}},\quad \mathbf {C} _{3}={\begin{bmatrix}0&1&0\\-1&0&0\\0&0&0\end{bmatrix} }}$ Te macierze mają następujące właściwości: ${\ Displaystyle \ mathbf {C} _ {i} ^ {\ textrm {T}} = - \ mathbf {C} _ {i}}$ (skośno-symetryczny); Zarówno ślad, jak i wyznacznik są zerowe; ${\ Displaystyle {\ tekst {ranga}} (\ mathbf {C} _ {i}) = 2}$; ${\ Displaystyle \ mathbf {C} _ {i} \ mathbf {C} _ {i} ^ {\ textrm {T}} = \ mathbf {P} _ {\ mathbf {e} _ {i}} ^ {^ {\osoba}}}$ (patrz poniżej); Prostopadłe macierz projekcji wektora jest przez . Macierz rzutowania na dopełnienie ortogonalne jest dana przez , gdzie jest macierzą jednostkową. W szczególnym przypadku , można to sprawdzić ${\displaystyle \mathbf {v} \neq \mathbf {0}}$${\ Displaystyle \ mathbf {P} _ {\ mathbf {v}} = \ mathbf {v} \ lewo (\ mathbf {v} ^ {\ textrm {T}} \ mathbf {v} \ prawej) ^ {-1 }\mathbf {v} ^{T}}$${\ Displaystyle \ mathbf {P} _ {\ mathbf {v}} ^ {^ {\ sprawca}} = \ mathbf {ja} - \ mathbf {P} _ {\ mathbf {v}}}$${\displaystyle \mathbf {ja}}$${\ Displaystyle \ mathbf {v} = \ mathbf {e} _ {i}}$ ${\ Displaystyle \ mathbf {P} _ {\ mathbf {e} _ {1}} ^ {^ {\ sprawca}} = {\ zacznij {bmatrix} 0 i 0 i 0 \ \ 0 i 1 i 0 \ \ 0 i 0 i 1 \ koniec {bmatrix}} \ quad \mathbf {P} _{\mathbf {e} _{2}}^{^{\perp }}={\begin{bmatrix}1&0&0&0\\0&0&0\\0&0&1\end{bmatrix}},\quad \ mathbf {P} _{\mathbf {e} _{3}}^{^{\perp }}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}}}$ Aby poznać inne właściwości macierzy rzutowania ortogonalnego, zobacz rzutowanie (algebra liniowa) .

Notacja indeksowa dla tensorów

Iloczyn krzyżowy można alternatywnie zdefiniować za pomocą symbolu Levi-Civita ε _ijk i iloczynu skalarnego η ^mi (= δ ^mi dla bazy ortonormalnej), które są przydatne w konwersji notacji wektorowej dla zastosowań tensorowych:

${\ Displaystyle \ mathbf {c} = \ mathbf {a \ razy b} \ Leftrightarrow \ c^ {m} = \ suma _ {i = 1} ^ {3} \ suma _ {j = 1} ^ {3} \sum _{k=1}^{3}\eta ^{mi}\varepsilon _{ijk}a^{j}b^{k}}$

gdzie indeksy odpowiadają składowym wektora. Ta charakterystyka iloczynu krzyżowego jest często wyrażana bardziej zwięźle przy użyciu konwencji sumowania Einsteina jako ${\displaystyle ja,j,k}$

${\ Displaystyle \ mathbf {c} = \ mathbf {a \ razy b} \ Leftrightarrow \ c ^ {m} = \ eta ^ {mi} \ varepsilon _ {ijk} a ^ {j} b ^ {k}}$

w którym powtarzające się indeksy są sumowane nad wartościami od 1 do 3. Ta reprezentacja jest inną formą skośno-symetrycznej reprezentacji iloczynu krzyżowego:

${\ Displaystyle \eta ^ {mi} \ varepsilon _ {ijk} a ^ {j} = [\ mathbf {a}] _ {\ razy}.}$

W mechanice klasycznej : przedstawienie iloczynu krzyżowego za pomocą symbolu Levi-Civita może spowodować, że symetrie mechaniczne będą oczywiste, gdy układy fizyczne są izotropowe . (Przykład: rozważmy cząstkę w potencjale prawa Hooke'a w trzech przestrzeniach, która może swobodnie oscylować w trzech wymiarach; żaden z tych wymiarów nie jest „specjalny” w żadnym sensie, więc symetrie leżą w pędzie pędu reprezentowanym przez produkt krzyżowy, który są jasno określone we wspomnianym powyżej oświadczeniu Levi-Civita).

Mnemoniczny

Słowo „xyzzy” może być użyte do zapamiętania definicji iloczynu krzyżowego.

Gdyby

${\ Displaystyle \ mathbf {a} = \ mathbf {b} \ razy \ mathbf {c}}$

gdzie:

${\ Displaystyle \ mathbf {a} = {\ zacząć {bmatrix} a_ {x} \ \ a_ {y} \ \ a_ {z} \ koniec {bmatrix}} \ \ mathbf {b} = {\ zacząć {bmatrix} }b_{x}\\b_{y}\\b_{z}\end{bmatrix}},\ \mathbf {c} ={\begin{bmatrix}c_{x}\\c_{y}\\c_ {z}\koniec{bmatrycy}}}$

następnie:

${\ Displaystyle a_ {x} = b_ {y} c_ {z}-b_ {z} c_ {y}}$

${\ Displaystyle a_ {y} = b_ {z} c_ {x}-b_ {x} c_ {z}}$

${\ Displaystyle a_ {z} = b_ {x} c_ {y}-b_ {y} c_ {x}.}$

Drugie i trzecie równanie można uzyskać z pierwszego, po prostu obracając indeksy dolne w pionie, x → y → z → x . Problem polega oczywiście na tym, jak zapamiętać pierwsze równanie, aw tym celu dostępne są dwie opcje: albo zapamiętać odpowiednie dwie przekątne schematu Sarrusa (te zawierające i ), albo zapamiętać sekwencję xyzzy.

Ponieważ pierwsza przekątna w schemacie Sarrusa jest tylko główną przekątną wspomnianej powyżej macierzy 3×3, pierwsze trzy litery słowa xyzzy można bardzo łatwo zapamiętać.

Wizualizacja krzyżowa

Podobnie jak w powyższym urządzeniu mnemonicznym, między dwoma wektorami w równaniu można wizualizować „krzyżyk” lub X. Może to być pomocne przy zapamiętaniu prawidłowej formuły międzyproduktowej.

Gdyby

${\ Displaystyle \ mathbf {a} = \ mathbf {b} \ razy \ mathbf {c}}$

następnie:

${\ Displaystyle \ mathbf {a} = {\ zacząć {bmatrix} b_ {x} \ \ b_ {y} \ \ b_ {z} \ koniec {bmatrix}} \ razy {\ zacząć {bmatrix} c_ {x} \ \c_{y}\\c_{z}\end{bmatryca}}.}$

Jeśli chcemy uzyskać wzór na po prostu odrzucamy i ze wzoru i sprowadzamy kolejne dwie składowe: ${\displaystyle a_{x}}$${\displaystyle b_{x}}$${\displaystyle c_{x}}$

${\ Displaystyle a_ {x} = {\ zacząć {bmatrix} b_ {y} \ \ b_ {z} \ koniec {bmatrix}} \ razy {\ zacząć {bmatrix} c_ {y} \ \ c_ {z} \ koniec {bmatryca}}.}$

Robiąc to, dla następnych dwóch elementów w dół należy „zawinąć” macierz tak, aby po składniku z pojawił się składnik x. Dla jasności, wykonując tę ​​operację dla , kolejne dwie składowe powinny być z i x (w tej kolejności). Natomiast dla kolejnych dwóch składowych należy przyjąć jako x i y. ${\displaystyle a_{y}}$${\displaystyle a_{y}}$${\displaystyle a_{z}}$

${\ Displaystyle a_ {y} = {\ zacznij {bmatrix} b_ {z} \ \ b_ {x} \ koniec {bmatrix}} \ razy {\ zacznij {bmatrix} c_ {z} \ \ c_ {x} \ koniec {bmatrix}},\ a_{z}={\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y }\end{bmatryca}}}$

W takim przypadku , jeśli wyobrazimy sobie operator krzyża jako wskazujący od elementu po lewej stronie do elementu po prawej stronie, możemy wziąć pierwszy element po lewej stronie i po prostu pomnożyć przez element, na który wskazuje krzyżyk w macierzy po prawej stronie. Następnie odejmujemy kolejny element w dół po lewej stronie, pomnożony przez element, na który wskazuje krzyżyk również tutaj. Daje to w efekcie naszą formułę – ${\displaystyle a_{x}}$${\displaystyle a_{x}}$

${\ Displaystyle a_ {x} = b_ {y} c_ {z}-b_ {z} c_ {y}.}$

Możemy to zrobić w ten sam sposób dla i konstruować powiązane z nimi formuły. ${\displaystyle a_{y}}$${\displaystyle a_{z}}$

Aplikacje

Produkt krzyżowy ma zastosowania w różnych kontekstach. Na przykład jest używany w geometrii obliczeniowej, fizyce i inżynierii. Poniżej znajduje się niewyczerpująca lista przykładów.

Geometria obliczeniowa

Iloczyn poprzeczny pojawia się przy obliczaniu odległości dwóch ukośnych linii (linie nie w tej samej płaszczyźnie) od siebie w przestrzeni trójwymiarowej.

Iloczyn krzyżowy może być użyty do obliczenia normalnej dla trójkąta lub wielokąta, operacji często wykonywanej w grafice komputerowej . Na przykład skręcenie wielokąta (zgodnie z ruchem wskazówek zegara lub przeciwnie do ruchu wskazówek zegara) wokół punktu wewnątrz wielokąta można obliczyć poprzez triangulację wielokąta (jak mówienie koła) i zsumowanie kątów (pomiędzy szprychami) za pomocą iloczynu krzyżowego, aby śledzić znak każdego kąta.

W Geometria obliczeniowa w płaszczyźnie produkt przekrój służy do określenia znaku kąta ostrego , określony przez trzy punkty i . Odpowiada on kierunkowi (w górę lub w dół) iloczynu poprzecznego dwóch współpłaszczyznowych wektorów określonych przez dwie pary punktów i . Znak kąta ostrego jest znakiem wyrażenia ${\displaystyle p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})}$${\displaystyle p_{3}=(x_{3},y_{3})}$${\displaystyle (p_{1},p_{2})}$${\displaystyle (p_{1},p_{3})}$

${\ Displaystyle P = (x_ {2}-x_ {1}) (y_ {3}-y_ {1})-(y_ {2}-y_ {1}) (x_ {3}-x_ {1}) ,}$

który jest podpisaną długością iloczynu poprzecznego dwóch wektorów.

W "prawostronnym" układzie współrzędnych, jeśli wynik wynosi 0, punkty są współliniowe ; jeśli jest dodatnia, trzy punkty tworzą dodatni kąt obrotu wokół od do , w przeciwnym razie kąt ujemny. Z innego punktu widzenia znak oznacza, czy leży na lewo, czy na prawo od linii${\displaystyle p_{1}}$${\displaystyle p_{2}}$${\displaystyle p_{3}}$${\displaystyle P}$${\displaystyle p_{3}}$${\displaystyle p_{1},p_{2}.}$

Iloczyn poprzeczny jest używany do obliczania objętości wielościanu, takiego jak czworościan lub równoległościan .

Kręt i moment obrotowy

Pędu L cząstki o danej pochodzenia zdefiniowana jako:

${\ Displaystyle \ mathbf {L} = \ mathbf {r} \ razy \ mathbf {p}}$

gdzie r jest wektorem położenia cząstki względem początku, p jest liniowym momentem pędu cząstki.

W ten sam sposób moment M siły F _B przyłożonej w punkcie B wokół punktu A jest podany jako:

${\ Displaystyle \ mathbf {M} _ {\ operatorname {A} } = \ mathbf {r} _ {\ operatorname {AB}} \ razy \ mathbf {F} _ {\ operatorname {B}} \,}$

W mechanice moment siły jest również nazywany momentem obrotowym i zapisywany jako${\displaystyle \mathbf {\tau}}$

Ponieważ pozycja r , liniowy pęd p i siła F są wektorami rzeczywistymi , zarówno moment pędu L, jak i moment siły M są pseudowektorami lub wektorami osiowymi .

Sztywny korpus

Iloczyn krzyżowy często pojawia się w opisie ruchów sztywnych. Dwa punkty P i Q na ciele sztywnym można powiązać za pomocą:

${\ Displaystyle \ mathbf {v} _ {P} - \ mathbf {v} _ {Q} = {\ pogrubienie {\ omega}} \ razy \ lewo (\ mathbf {R} _ {P} - \ mathbf {r } _{Q}\prawo)\,}$

gdzie jest położenie punktu, jego prędkość i prędkość kątowa ciała . ${\displaystyle \mathbf {r}}$${\displaystyle \mathbf {v}}$${\displaystyle {\boldsymbol {\omega}}}$

Ponieważ położenie i prędkość są wektorami rzeczywistymi , prędkość kątowa jest pseudowektorem lub wektorem osiowym . ${\displaystyle \mathbf {r}}$${\displaystyle \mathbf {v}}$${\displaystyle {\boldsymbol {\omega}}}$

Siła Lorentza

Iloczyn krzyżowy służy do opisania siły Lorentza doświadczanej przez poruszający się ładunek elektryczny q _e :

${\ Displaystyle \ mathbf {F} = q_ {e} \ lewo (\ mathbf {E} + \ mathbf {v} \ razy \ mathbf {B} \ prawej)}$

Ponieważ prędkość v , siła F i pole elektryczne E są wektorami rzeczywistymi , pole magnetyczne B jest pseudowektorem .

Inne

W rachunku wektorowym iloczyn krzyżowy jest używany do zdefiniowania wzoru na zwinięcie operatora wektora .

Sztuczka polegająca na przepisaniu iloczynu krzyżowego w kategoriach mnożenia macierzy pojawia się często w geometrii epipolarnej i wielowidokowej , w szczególności przy wyprowadzaniu ograniczeń dopasowania.

Jako produkt zewnętrzny

Produkt krzyżowy można zdefiniować w kategoriach produktu zewnętrznego. Można go uogólnić na produkt zewnętrzny w innych niż trzy wymiary. Ten widok pozwala na naturalną geometryczną interpretację produktu krzyżowego. W algebrze zewnętrznej iloczynem zewnętrznym dwóch wektorów jest dwuwektor. Dwuwektor jest zorientowanym elementem płaskim, podobnie jak wektor jest zorientowanym elementem liniowym. Biorąc pod uwagę dwa wektory a i b , można zobaczyć bivector a ∧ b jako zorientowane równoległoboku trwała przez i b . Iloczyn krzyżowy jest następnie otrzymywany poprzez wzięcie gwiazdy Hodge'a dwuwektora a ∧ b , mapując 2 wektory na wektory:

${\ Displaystyle a \ razy b = \ gwiazda (a \ klin b) \,.}$

Można to traktować jako zorientowany element wielowymiarowy „prostopadle” do dwuwektora. Tylko w trzech wymiarach wynik jest zorientowanym elementem jednowymiarowym – wektorem – podczas gdy na przykład w czterech wymiarach podwójny dwuwymiarowy Hodge jest dwuwymiarowy – dwuwektorowy. Tak więc, tylko w trzech wymiarach można wektor iloczynu i B są określone jako wektor podwójny do bivector a ∧ b : prostopadle do bivector z orientacji w zależności od bezstronności układ współrzędnych, ma także taką samą wielkość względem do zespołu wektor normalny, jak na ∧ b ma w stosunku do bivector jednostkowej; dokładnie właściwości opisane powyżej.

Praworęczność

Spójność

Kiedy prawa fizyki są zapisywane jako równania, można dokonać dowolnego wyboru układu współrzędnych, w tym ręczności. Należy uważać, aby nigdy nie zapisywać równania, w którym obie strony nie zachowują się jednakowo we wszystkich transformacjach, które należy wziąć pod uwagę. Na przykład, jeśli jedna strona równania jest iloczynem krzyżowym dwóch wektorów biegunowych, należy wziąć pod uwagę, że wynikiem jest wektor osiowy . Dlatego, aby zachować spójność, druga strona również musi być wektorem osiowym. Bardziej ogólnie, wynik iloczynu krzyżowego może być wektorem biegunowym lub wektorem osiowym, w zależności od typu jego argumentów (wektory biegunowe lub wektory osiowe). Mianowicie wektory biegunowe i wektory osiowe są ze sobą powiązane w następujący sposób przy zastosowaniu iloczynu poprzecznego:

• wektor biegunowy × wektor biegunowy = wektor osiowy
• wektor osiowy × wektor osiowy = wektor osiowy
• wektor biegunowy × wektor osiowy = wektor biegunowy
• wektor osiowy × wektor biegunowy = wektor biegunowy

lub symbolicznie

• biegunowy × biegunowy = osiowy
• osiowe × osiowe = osiowe
• biegunowy × osiowy = biegunowy
• osiowy × biegunowy = biegunowy

Ponieważ iloczyn krzyżowy może być również wektorem biegunowym, może nie zmieniać kierunku z lustrzanym odbiciem. Dzieje się tak, zgodnie z powyższymi zależnościami, jeśli jeden z argumentów jest wektorem biegunowym, a drugi wektorem osiowym (np. iloczyn krzyżowy dwóch wektorów biegunowych). Na przykład potrójny produkt wektorowy obejmujący trzy wektory polarne jest wektorem polarnym.

Podejście bez użycia rąk jest możliwe przy użyciu algebry zewnętrznej.

Paradoks bazy ortonormalnej

Niech ( i , j , k ) będzie bazą ortonormalną. Wektory i , j oraz k nie zależą od orientacji przestrzeni. Można je nawet zdefiniować w przypadku braku orientacji. Nie mogą więc być wektorami osiowymi. Ale jeśli i oraz j są wektorami biegunowymi, to k jest wektorem osiowym dla i × j = k lub j × i = k . To paradoks.

„Osiowy” i „biegunowy” są fizycznymi kwalifikatorami wektorów fizycznych ; to znaczy wektory, które reprezentują wielkości fizyczne, takie jak prędkość lub pole magnetyczne. Wektory i , j oraz k są wektorami matematycznymi, ani osiowymi, ani biegunowymi. W matematyce iloczynem krzyżowym dwóch wektorów jest wektor. Nie ma sprzeczności.

Uogólnienia

Istnieje kilka sposobów na uogólnienie iloczynu krzyżowego na wyższe wymiary.

Algebra kłamstwa

Produkt krzyżowy może być postrzegany jako jeden z najprostszych produktów Liego, a zatem jest uogólniony przez algebry Liego , które są aksjomatyzowane jako produkty binarne spełniające aksjomaty wieloliniowości, symetrii skośnej i tożsamości Jacobiego. Istnieje wiele algebr Liego, a ich badanie jest główną dziedziną matematyki, zwaną teorią Liego .

Na przykład, algebra Heisenberga daje inną strukturę algebry Liego na podstawie iloczynu${\ Displaystyle \ mathbf {R} ^ {3}.}$${\displaystyle \{x,y,z\}}$${\displaystyle [x,y]=z,[x,z]=[y,z]=0.}$

Kwateryny

Iloczyn krzyżowy można również opisać w kategoriach kwaternionów . Ogólnie, jeśli wektor [ a ₁ , a ₂ , a ₃ ] jest reprezentowany jako kwaternion a ₁ i + a ₂ j + a ₃ k , iloczyn krzyżowy dwóch wektorów można otrzymać biorąc ich iloczyn jako kwaternionów i usuwając rzeczywista część wyniku. Część rzeczywista będzie ujemnym iloczynem skalarnym dwóch wektorów.

Oktoniony

Produkt krzyżowy dla wektorów 7-wymiarowych można uzyskać w ten sam sposób, używając oktonionów zamiast kwaternionów. Nieistnienie nietrywialnych iloczynów wektorowych o wartościach wektorowych dwóch wektorów w innych wymiarach jest związane z wynikiem twierdzenia Hurwitza, że jedynymi znormalizowanymi algebrami dzielenia są te, które mają wymiar 1, 2, 4 i 8.

Produkt zewnętrzny

W wymiarze ogólnym nie ma bezpośredniego odpowiednika binarnego produktu krzyżowego, który daje konkretnie wektor. Istnieje jednak iloczyn zewnętrzny, który ma podobne właściwości, z tą różnicą, że iloczyn zewnętrzny dwóch wektorów jest teraz 2-wektorem zamiast zwykłego wektora. Jak wspomniano powyżej, iloczyn krzyżowy może być interpretowany jako iloczyn zewnętrzny w trzech wymiarach za pomocą operatora gwiazdy Hodge'a do mapowania wektorów 2 na wektory. Dual Hodge'a iloczynu zewnętrznego daje wektor ( n − 2) , który jest naturalnym uogólnieniem iloczynu krzyżowego w dowolnej liczbie wymiarów.

Iloczyn zewnętrzny i iloczyn skalarny można łączyć (poprzez sumowanie) w celu utworzenia iloczynu geometrycznego w algebrze geometrycznej.

Produkt zewnętrzny

Jak wspomniano powyżej, produkt krzyżowy może być interpretowany w trzech wymiarach jako podwójny Hodge'a produktu zewnętrznego. W dowolnym skończonym n wymiarach, podwójny Hodge'a iloczynu zewnętrznego n − 1 wektorów jest wektorem. Tak więc, zamiast operacji binarnej, w dowolnych skończonych wymiarach, iloczyn krzyżowy jest uogólniany jako podwójny Hodge'a iloczynu zewnętrznego pewnych danych n − 1 wektorów. To uogólnienie nazywa się produktem zewnętrznym .

Produkt komutatora

Interpretacja trójwymiarowej przestrzeni wektorowej algebry jako 2-wektorowej (nie 1-wektorowej) podalgebry trójwymiarowej algebry geometrycznej, gdzie , , i , iloczyn krzyżowy odpowiada dokładnie iloczynowi komutatora w algebrze geometrycznej i obu użyj tego samego symbolu . Iloczyn komutatora jest zdefiniowany dla 2 wektorów oraz w algebrze geometrycznej jako: ${\displaystyle \mathbf {i} =\mathbf {e_{2}} \mathbf {e_{3}}}$${\displaystyle \mathbf {j} =\mathbf {e_{1}} \mathbf {e_{3}}}$${\ Displaystyle \ mathbf {k} = \ mathbf {e_ {1}} \ mathbf {e_ {2}}}$${\displaystyle \times}$${\ Displaystyle A}$${\ Displaystyle B}$

${\ Displaystyle A \ razy B = {\ tfrac {1} {2}} (AB-BA)}$

gdzie jest produkt geometryczny. ${\displaystyle AB}$

Iloczyn komutatora można uogólnić na dowolne wielowektory w trzech wymiarach, co skutkuje wielowektorem składającym się tylko z elementów klas 1 (1-wektory/ prawdziwe wektory ) i 2 (2-wektory/pseudowektory). Podczas gdy iloczyn komutatora dwóch 1-wektorów jest rzeczywiście taki sam jak iloczyn zewnętrzny i daje 2-wektor, komutator 1-wektora i 2-wektora daje prawdziwy wektor, odpowiadający zamiast tego lewemu i prawemu skróceniu w algebra geometryczna. Iloczyn komutatora dwóch dwuwektorów nie ma odpowiadającego mu iloczynu równoważnego, dlatego iloczyn komutatora jest zdefiniowany w pierwszej kolejności dla dwuwektorów. Co więcej, potrójny iloczyn komutatora trzech 2-wektorów jest taki sam, jak potrójny iloczyn wektorowy tych samych trzech pseudowektorów w algebrze wektorowej. Jednak komutator potrójną trzy 1-wektorów geometryczną Algebra jest zamiast ujemny z wektora potrójną tych samych trzech prawdziwych wektorów w wektorze Algebra.

Uogólnienia do wyższych wymiarów zapewnia ten sam iloczyn komutatora dwuwektorów w wyższych wymiarach geometrycznych, ale wektory dwuwymiarowe nie są już pseudowektorami. Tak jak iloczyn komutatora/iloczyn krzyżowy dwuwektorów w trzech wymiarach odpowiada najprostszej algebrze Liego , dwuwektorowe podalgebry algebry geometrycznej wyższych wymiarów wyposażonej w iloczyn komutatora również odpowiadają algebrom Liego. Podobnie jak w trzech wymiarach, iloczyn komutatora można dalej uogólnić na dowolne wielowektory.

Algebra wieloliniowa

W kontekście algebry wieloliniowej iloczyn krzyżowy może być postrzegany jako (1,2)-tensor ( tensor mieszany , konkretnie mapa dwuliniowa ) uzyskany z trójwymiarowej postaci objętości , a (0,3)-tensor, poprzez podniesienie indeksu .

Szczegółowo, trójwymiarowa forma objętości definiuje produkt , biorąc wyznacznik macierzy podanej przez te 3 wektory. Przez dualność jest to równoważne funkcji (ustalenie dowolnych dwóch danych wejściowych daje funkcję przez obliczenie na trzecim wejściu) oraz w obecności iloczynu skalarnego (takiego jak iloczyn skalarny; bardziej ogólnie, niezdegenerowana forma dwuliniowa), mamy izomorfizm i stąd otrzymujemy mapę będącą iloczynem krzyżowym: a (0,3)-tensor (3 wejścia wektorowe, wyjście skalarne) został przekształcony w (1,2)-tensor (2 wejścia wektorowe, 1 wyjście wektorowe) przez „podnoszenie indeksu”. ${\ Displaystyle V \ razy V \ razy V \ do \ mathbf {R},}$${\ Displaystyle V \ razy V \ do V ^ {*},}$${\ Displaystyle V \ do \ mathbf {R}}$${\ Displaystyle V \ do V ^ {*},}$${\ Displaystyle V \ razy V \ do V}$

Przekładając powyższą algebrę na geometrię, funkcja „objętość równoległościanu zdefiniowanego przez ” (gdzie dwa pierwsze wektory są ustalone, a ostatni jest wejściem), która definiuje funkcję , może być reprezentowana jednoznacznie jako iloczyn skalarny z wektorem: ten wektor jest iloczynem krzyżowym Z tej perspektywy iloczyn krzyżowy jest zdefiniowany przez potrójny iloczyn skalarny ,${\displaystyle (a,b,-)}$${\ Displaystyle V \ do \ mathbf {R}}$${\displaystyle a\razy b.}$${\ Displaystyle \ operatorname {Tom} (a, b, c) = (a \ razy b) \ cdot c.}$

W ten sam sposób w wyższych wymiarach można zdefiniować uogólnione iloczyny krzyżowe poprzez podniesienie wskaźników n- wymiarowej postaci objętości, która jest -tensorem. Najbardziej bezpośrednie uogólnienia produktu krzyżowego polegają na zdefiniowaniu: ${\ Displaystyle (0, n)}$

• -tensor, co do którego wprowadzany wektor i podaje jako wyjścia 1 wektorem - -ary wektor wartościami produktu lub${\ Displaystyle (1, n-1)}$${\displaystyle n-1}$${\displaystyle (n-1)}$
• a -tensor, który przyjmuje jako wejście 2 wektory i daje jako wyjście tensor skośno-symetryczny rzędu n − 2 – iloczyn binarny o rządzie n − 2 wartości tensora. Można również zdefiniować -tensory dla innych k .${\ Displaystyle (n-2,2)}$${\ Displaystyle (k, nk)}$

Wszystkie te iloczyny są wieloliniowe i skośno-symetryczne i można je zdefiniować w kategoriach wyznacznika i parzystości .

Produkt -ary można opisać w następujący sposób: podane wektory na określenie ich uogólnionym produkt jako: ${\displaystyle (n-1)}$${\displaystyle n-1}$${\displaystyle v_{1},\kropki,v_{n-1}}$${\ Displaystyle \ mathbf {R} ^ {n}}$${\ Displaystyle v_ {n} = v_ {1} \ razy \ cdots \ razy v_ {n-1}}$

• prostopadła do hiperpłaszczyzny określonej przez ${\displaystyle v_{i},}$
• wielkość jest objętością równoległoboku określoną przez, którą można obliczyć jako wyznacznik grama${\displaystyle v_{i},}$${\displaystyle v_{i},}$
• zorientowany tak, że jest zorientowany pozytywnie.${\displaystyle v_{1},\kropki,v_{n}}$

Jest unikalne multilinear naprzemiennie produkt rozpoznawaną , itd cyklicznych permutacji indeksów. ${\ Displaystyle e_ {1} \ razy \ cdots \ razy e_ {n-1} = e_ {n}}$${\ Displaystyle e_ {2} \ razy \ cdots \ razy e_ {n} = e_ {1},}$

We współrzędnych można podać wzór na ten -arny analog iloczynu krzyżowego w R ⁿ przez: ${\displaystyle (n-1)}$

${\ Displaystyle \ bigwedge _ {i = 0} ^ {n-1} \ mathbf {v} _ {i} = {\ zacząć {vmatrix} v_ {1} {} ^ {1} i \ cdots V_ {1} {}^{n}\\\vdots &\ddots &\vdots \\v_{n-1}{}^{1}&\cdots &v_{n-1}{}^{n}\\\mathbf { e} _{1}&\cdots &\mathbf {e} _{n}\end{vmatrix}}.}$

Wzór ten jest identyczny w budowie do determinanty wzoru dla normalnych produktu poprzecznym na R ^3, z tym wyjątkiem, wiersz wektorów bazowych jest ostatni wiersz wyznacznika raczej niż pierwszy. Powodem tego jest zapewnienie, że uporządkowane wektory ( v ₁ , ..., v _{n −1} , Λ^{n –1}
_i=0v _i ) mieć orientację dodatnią w odniesieniu do ( e ₁ , ..., e _n ). Jeśli n jest nieparzyste, ta modyfikacja pozostawia niezmienioną wartość, więc ta konwencja jest zgodna z normalną definicją iloczynu binarnego. Jednak w przypadku, gdy n jest parzyste, należy zachować rozróżnienie. Ta -arowa forma ma wiele takich samych właściwości jak iloczyn wektorowy: jest naprzemienny i liniowy w swoich argumentach, jest prostopadły do ​​każdego argumentu, a jego wielkość daje hiperobjętość obszaru ograniczonego argumentami. I tak jak iloczyn wektorowy wektorowy, może być zdefiniowany w sposób niezależny od współrzędnych jako podwójna liczba Hodge'a iloczynu klinowego argumentów. ${\displaystyle (n-1)}$

Historia

W 1773 roku Joseph-Louis Lagrange wprowadził formę składową zarówno produktów kropkowych, jak i krzyżowych, aby zbadać czworościan w trzech wymiarach. W 1843 roku William Rowan Hamilton wprowadził iloczyn kwaternionów , a wraz z nim terminy „wektor” i „skalar”. Biorąc pod uwagę dwa kwaterniony [0, u ] i [0, v ] , gdzie u i v są wektorami w R ³ , ich iloczyn kwaternionów można podsumować jako [− u ⋅ v , u × v ] . James Clerk Maxwell użył narzędzi kwaternionów Hamiltona do opracowania swoich słynnych równań elektromagnetyzmu iz tego i innych powodów kwaternionów przez pewien czas stanowiły istotną część edukacji fizyki.

W 1878 roku William Kingdon Clifford opublikował swoje Elements of Dynamic, który był jak na owe czasy zaawansowanym tekstem. Zdefiniował dwóch wektorów mieć wielkość równą powierzchni do równoległoboku , w którym są dwa boki, i w kierunku prostopadłym do ich płaszczyzny.

Oliver Heaviside i Josiah Willard Gibbs również uważali, że metody kwaternionowe są zbyt kłopotliwe, często wymagając wyodrębnienia części skalarnej lub wektorowej wyniku. Tak więc około czterdzieści lat po iloczynie kwaternionowym wprowadzono iloczyn skalarny i iloczyn krzyżowy — do gorącej opozycji. Kluczem do (ostatecznej) akceptacji była efektywność nowego podejścia, pozwalająca Heaviside'owi zredukować równania elektromagnetyzmu z oryginalnych 20 Maxwella do czterech powszechnie spotykanych obecnie.

W dużej mierze niezależna od tego rozwoju i w dużej mierze niedoceniana w tamtych czasach, Hermann Grassmann stworzył algebrę geometryczną niezwiązaną z drugim lub trzecim wymiarem, w której główną rolę odgrywał produkt zewnętrzny. W 1853 roku Augustin-Louis Cauchy , współczesny Grassmannowi, opublikował artykuł o kluczach algebraicznych, które były używane do rozwiązywania równań i miały takie same właściwości mnożenia jak iloczyn krzyżowy. Clifford połączył algebry Hamiltona i Grassmanna, aby stworzyć algebrę Clifforda , gdzie w przypadku wektorów trójwymiarowych dwuwektor utworzony z dwóch wektorów dualizuje się do wektora, odtwarzając w ten sposób iloczyn krzyżowy.

Notacja krzyżowa i nazwa „produkt krzyżowy” zaczęły się od Gibbsa. Pierwotnie pojawiły się one w prywatnie opublikowanych notatkach dla jego uczniów w 1881 roku jako Elementy analizy wektorowej . Przydatność dla mechaniki zauważył Aleksandr Kotelnikov . Notacja Gibbsa i nazwa „produkt krzyżowy” dotarły później do szerokiego grona odbiorców dzięki Vector Analysis , podręcznikowi autorstwa Edwina Bidwella Wilsona , byłego studenta. Wilson przearanżował materiał z wykładów Gibbsa wraz z materiałem z publikacji Heaviside'a, Föppsa i Hamiltona. Analizę wektorową podzielił na trzy części:

Po pierwsze, ta, która dotyczy dodawania oraz iloczynów skalarnych i wektorowych wektorów. Po drugie, to, co dotyczy rachunku różniczkowego i całkowego w jego relacjach z funkcjami skalarnymi i wektorowymi. Po trzecie, to, które zawiera teorię liniowej funkcji wektorowej.

Zdefiniowano dwa główne rodzaje mnożenia wektorów, które nazwano następująco:

• Bezpośredni , skalar lub punkt dwóch wektorów
• Skosu , wektor lub przekrój dwóch wektorów

Zbadano również kilka rodzajów potrójnych produktów i produktów więcej niż trzech wektorów. Uwzględniono również wspomnianą wyżej potrójną ekspansję produktową.

Zobacz też

• Iloczyn kartezjański – Iloczyn dwóch zestawów
• Algebra geometryczna: systemy obrotowe
• Wiele produktów krzyżowych — produkty zawierające więcej niż trzy wektory
• Mnożenie wektorów
• Czteroosobowy produkt
• × (symbol)

Uwagi

Bibliografia

Bibliografia

• Cajori, Florian (1929). Historia notacji matematycznych Tom II . Wydawnictwo Sądu Otwartego . P. 134. Numer ISBN 978-0-486-67766-8.
• EA Milne (1948) Vectorial Mechanics , rozdział 2: Vector Product, s. 11-31, Londyn: Methuen Publishing .
• Wilson, Edwin Bidwell (1901). Analiza wektorowa: Podręcznik dla studentów matematyki i fizyki, oparty na wykładach J. Willarda Gibbsa . Wydawnictwo Uniwersytetu Yale .
• T. Levi-Civita; U. Amaldi (1949). Lezioni di meccanica razionale (po włosku). Bolonia: redaktor Zanichelli.

Zewnętrzne linki

• „Produkt krzyżowy” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• Szybkie wyprowadzenie geometryczne i interpretacja produktów krzyżowych
• Interaktywny samouczek stworzony na Uniwersytecie Syracuse – (wymaga java )
• W. Kahana (2007). Produkty krzyżowe i rotacje w 2 i 3 przestrzeni euklidesowej. Uniwersytet Kalifornijski w Berkeley (PDF).
• Produkt wektorowy , Mathcentre (Wielka Brytania), 2009