Dwuwektor - Bivector

W matematyce , A bivector lub 2 wektor jest ilość w zewnętrznej Algebra lub geometryczne Algebra który rozciąga się pomysł skalarnych i wektorów . Jeśli skalar jest wielkością zerową stopnia, a wektor jest wielkością pierwszego stopnia, to dwuwektor można uznać za wielkość drugiego stopnia. Dwuwektory mają zastosowanie w wielu dziedzinach matematyki i fizyki. Są one powiązane z liczbami zespolonymi w dwóch wymiarach oraz z pseudowektorami i kwaternionami w trzech wymiarach. Mogą być używane do generowania obrotów w dowolnej liczbie wymiarów i są użytecznym narzędziem do klasyfikowania takich obrotów. Są również używane w fizyce , wiążąc ze sobą szereg niepowiązanych w inny sposób wielkości.

Dwuwektory są generowane przez iloczyn zewnętrzny na wektorach: przy danych dwóch wektorach a i b ich iloczyn zewnętrzny a ∧ b jest dwuwektorem, podobnie jak suma dowolnych dwuwektorów. Nie wszystkie dwuwektory można wygenerować jako pojedynczy produkt zewnętrzny. Dokładniej, dwuwektor, który można wyrazić jako produkt zewnętrzny, nazywa się prostym ; w maksymalnie trzech wymiarach wszystkie dwuwektory są proste, ale w wyższych wymiarach tak nie jest. Zewnętrzny iloczyn dwóch wektorów jest przemienny , więc b ∧ a jest negacją dwuwektora a ∧ b , co daje przeciwną orientację, a a ∧ a jest dwuwektorem zerowym.

Geometrycznie prosty dwuwektor może być interpretowany jako zorientowany segment płaszczyzny , podobnie jak wektory można traktować jako skierowane segmenty linii . Bivector ∧ b ma wielkość równą obszarze równoległoboku z krawędzi a i b , ma nastawienie płaszczyzny trwała przez i B , i ma orientację jest sens rotacji że dostosowania z b .

W kategoriach laika każda powierzchnia jest tym samym dwuwektorem, jeśli ma ten sam obszar, taką samą orientację i jest równoległa do tej samej płaszczyzny (patrz rysunek).

Historia

Dwuwektor został po raz pierwszy zdefiniowany w 1844 roku przez niemieckiego matematyka Hermanna Grassmanna w algebrze zewnętrznej jako wynik iloczynu zewnętrznego dwóch wektorów. Zaledwie rok wcześniej w Irlandii William Rowan Hamilton odkrył kwaterniony . Dopiero angielski matematyk William Kingdon Clifford w 1888 roku dodał produkt geometryczny do algebry Grassmanna, włączając w to idee zarówno Hamiltona, jak i Grassmanna, i założył algebrę Clifforda , dzięki czemu dwuwektor, jaki jest dziś znany, został w pełni zrozumiany.

Mniej więcej w tym czasie Josiah Willard Gibbs i Oliver Heaviside opracowali rachunek wektorowy , który zawierał oddzielne iloczyny krzyżowe i iloczyny skalarne pochodzące z mnożenia kwaternionów. Sukces rachunku wektorowego i książki Vector Analysis autorstwa Gibbsa i Wilsona spowodował, że spostrzeżenia Hamiltona i Clifforda były przez długi czas pomijane, ponieważ większość XX-wiecznej matematyki i fizyki była formułowana w terminach wektorowych. Gibbs używał wektorów, aby wypełnić rolę dwuwektorów w trzech wymiarach i używał „dwektora” do opisania niepowiązanej ilości, co czasami było kopiowane. Dzisiaj dwuwektor jest w dużej mierze przedmiotem badań w algebrze geometrycznej, algebrze Clifforda nad rzeczywistymi lub złożonymi przestrzeniami wektorowymi o formie kwadratowej . Jego odrodzenie kierował David Hestenes, który wraz z innymi zastosował algebrę geometryczną do szeregu nowych zastosowań w fizyce .

Pochodzenie

W tym artykule dwuwektor będzie rozpatrywany tylko w rzeczywistych algebrach geometrycznych. W praktyce nie stanowi to dużego ograniczenia, ponieważ wszystkie użyteczne zastosowania są wyciągane z takich algebr. O ile nie zaznaczono inaczej, wszystkie przykłady mają metrykę euklidesową, a więc dodatnio określoną formę kwadratową .

Algebra geometryczna i iloczyn geometryczny

Dwuwektor wynika z definicji iloczynu geometrycznego w przestrzeni wektorowej. Dla wektorów a , b i c iloczyn geometryczny na wektorach definiuje się następująco:

Łączność

${\ Displaystyle (\ mathbf {ab} ) \ mathbf {c} = \ mathbf {a} (\ mathbf {BC})}$

Dystrybucja lewa i prawa

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a} (\ mathbf {b} + \ mathbf {c} ) i = \ mathbf {ab} + \ mathbf {ac} \\ (\ mathbf {b} +\ mathbf {c} )\mathbf {a} &=\mathbf {ba} +\mathbf {ca} \end{wyrównany}}}$

Skurcz

${\ Displaystyle {\ mathbf {a}} ^ {2} = Q (\ mathbf {a} ) = \ epsilon _ {\ mathbf {a}} {\ po lewej | \ mathbf {a} \ po prawej |} ^ {2 }}$

Gdzie Q jest formą kwadratową, | | jest wielkością od i ε jest podpis metryczny . Dla przestrzeni z metryką euklidesową ϵ _a wynosi 1, więc można je pominąć, a warunek skrócenia przyjmuje _postać :

${\ Displaystyle {\ mathbf {a}} ^ {2} = {\ lewo | \ mathbf {a} \ prawo |} ^ {2}}$

Produkt do wnętrz

Z asocjatywności a ( ab ) = a ² b , a skalar razy b . Gdy b nie jest równoległe, a zatem nie jest skalarną wielokrotnością a , ab nie może być skalarem. Ale

${\ Displaystyle {\ Frac {1} {2}} (\ mathbf {ab} + \ mathbf {ba} ) = {\ Frac {1} {2}} \ lewo ((\ mathbf {a} + \ mathbf { b} )^{2}-\mathbf {a} ^{2}-\mathbf {b} ^{2}\right)}$

jest sumą skalarów, a więc skalarem. Z prawa cosinusów na trójkącie utworzonym przez wektory jego wartość wynosi | | | b | cos  θ , gdzie θ jest kątem między wektorami. Jest zatem identyczny z iloczynem wewnętrznym między dwoma wektorami i jest napisany w ten sam sposób,

${\ Displaystyle \ mathbf {a} \ cdot \ mathbf {b} = {\ Frac {1} {2}} (\ mathbf {ab} + \ mathbf {ba}).}$

Jest symetryczny, skalarny i może być użyty do określenia kąta między dwoma wektorami: w szczególności jeśli a i b są ortogonalne, iloczyn wynosi zero.

Produkt zewnętrzny

Tak jak iloczyn wewnętrzny może być sformułowany jako symetryczna część iloczynu geometrycznego innej ilości, wyrób zewnętrzny (czasami znany jako wyrób „klinowy” lub „postępowy”) może być sformułowany jako jego część antysymetryczna :

${\ Displaystyle \ mathbf {a} \ klin \ mathbf {b} = {\ Frac {1} {2}} (\ mathbf {ab} - \ mathbf {ba})}$

Jest antysymetryczna w a i b

${\ Displaystyle \ mathbf {b} \ klin \ mathbf {a} = {\ Frac {1} {2}} (\ mathbf {ba} - \ mathbf {ab}) = - {\ Frac {1} {2} }(\mathbf {ab} -\mathbf {ba} )=-\mathbf {a} \wedge \mathbf {b} }$

oraz przez dodanie:

${\ Displaystyle \ mathbf {a} \ cdot \ mathbf {b} + \ mathbf {a} \ klin \ mathbf {b} = {\ Frac {1} {2}} (\ mathbf {ab} + \ mathbf {ba } )+{\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=\mathbf {ab} }$

Oznacza to, że iloczyn geometryczny jest sumą symetrycznego iloczynu wewnętrznego i antysymetrycznego iloczynu zewnętrznego.

Aby zbadać naturę a ∧ b , rozważ wzór

${\ Displaystyle (\ mathbf {a} \ cdot \ mathbf {b} ) ^ {2} - (\ mathbf {a} \ klin \ mathbf {b}) ^ {2} = \ mathbf {a} ^ {2} \mathbf {b} ^{2},}$

który używając pitagorejskiej tożsamości trygonometrycznej daje wartość ( a ∧ b ) ²

${\ Displaystyle (\ mathbf {a} \ klin \ mathbf {b}) ^ {2} = (\ mathbf {a} \ cdot \ mathbf {b}) ^ {2} - \ mathbf {a} ^ {2} \mathbf {b} ^{2}=\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}(\cos ^{2}\theta - 1)=-\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}\sin ^{2}\theta }$

Przy ujemnym kwadracie nie może to być wielkość skalarna ani wektorowa, więc jest to nowy rodzaj obiektu, dwuwektor . Ma wielkość | | | b | | grzech  θ | , gdzie θ jest kątem między wektorami, a więc jest zerem dla wektorów równoległych.

Aby odróżnić je od wektorów, dwuwektory są tutaj napisane pogrubionymi literami, na przykład:

${\ Displaystyle \ mathbf {A} = \ mathbf {a} \ klin \ mathbf {b} =- \ mathbf {b} \ klin \ mathbf {a} \,}$

chociaż stosowane są inne konwencje, w szczególności wektory i dwuwektory są elementami algebry geometrycznej.

Nieruchomości

Przestrzeń ⋀ ² R ⁿ

Algebra wygenerowana przez iloczyn geometryczny to algebra geometryczna w przestrzeni wektorowej. Dla euklidesowej przestrzeni wektorowej jest to zapisane lub Cl _n ( R ), gdzie n jest wymiarem przestrzeni wektorowej R ⁿ . Cl _n ( R ) jest zarówno przestrzenią wektorową, jak i algebrą, generowaną przez wszystkie iloczyny pomiędzy wektorami w R ⁿ , a więc zawiera wszystkie wektory i dwuwektory. Dokładniej jako przestrzeń wektorowa zawiera wektory i dwuwektory jako podprzestrzenie liniowe , ale nie podalgebry (ponieważ iloczyn geometryczny dwóch wektorów nie jest na ogół innym wektorem). Przestrzeń wszystkich dwuwektorów jest zapisana ⋀ ² R ⁿ . ${\ Displaystyle {\ Mathcal {G}} _ {n}}$

Parzysta podalgebra

Podalgebra generowana przez dwuwektory jest parzystą podalgebrą algebry geometrycznej, zapisaną Cl⁺
_n( R ). Algebra ta wynika z uwzględnienia wszystkich iloczynów skalarów i dwuwektorów generowanych przez iloczyn geometryczny. Ma wymiar 2 ^{n −1} i zawiera ⋀ ² R ⁿ jako podprzestrzeń liniową o wymiarze 1/2n ( n − 1) ( liczba trójkątna ). W dwóch i trzech wymiarach podalgebra parzysta zawiera tylko skalary i dwuwektory, a każdy z nich jest szczególnie interesujący. W dwóch wymiarach równomierne podalgebrą jest izomorficzny z liczb zespolonych , C , podczas gdy na trzech jest izomorficzny w Quaternions , H . Mówiąc bardziej ogólnie, parzysta podalgebra może być używana do generowania obrotów w dowolnym wymiarze i może być generowana przez dwuwektory w algebrze.

Ogrom

Jak zauważono w poprzedniej sekcji, wielkość prostego dwuwektora, czyli takiego, który jest iloczynem zewnętrznym dwóch wektorów a i b , wynosi | | | b | sin θ , gdzie θ jest kątem między wektorami. Jest napisane | B |, gdzie B jest dwuwektorem.

W przypadku dwuwektorów ogólnych wielkość można obliczyć przyjmując normę dwuwektora rozpatrywanego jako wektor w przestrzeni ⋀ ² R ⁿ . Jeśli wielkość wynosi zero, to wszystkie składowe dwuwektora są zerowe, a dwuwektor jest dwuwektorem zerowym, który jako element algebry geometrycznej jest równy zeru skalarnemu.

Dwuwektory jednostkowe

Dwuwektor jednostkowy to taki, który ma wielkość jednostkową. Można go wyprowadzić z dowolnego niezerowego dwuwektora, dzieląc dwuwektor przez jego wielkość, czyli

${\ Displaystyle {\ Frac {\ mathbf {B}} {\ po lewej | \ mathbf {B} \ po prawej |}}.}$

Na szczególną uwagę zasługują dwuwektory jednostkowe utworzone z produktów o podstawie standardowej . Jeśli e _i i e _j są różnymi bazowymi wektorami, to iloczyn e _i ∧ e _j jest dwuwektorem. Ponieważ wektory są ortogonalne , jest to po prostu e _i e _j , zapisane e _ij , z jednostkową wielkością , ponieważ wektory są wektorami jednostkowymi . Zbiór wszystkich takich dwuwektorów stanowi bazę dla ⋀ ² R ⁿ . Na przykład w czterech wymiarach podstawą dla ⋀ ² R ⁴ jest ( e ₁ e ₂ , e ₁ e ₃ , e ₁ e ₄ , e ₂ e ₃ , e ₂ e ₄ , e ₃ e ₄ ) lub ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ).

Proste dwuwektory

Produktem zewnętrznym dwóch wektorów jest dwuwektor, ale nie wszystkie dwuwektory są produktami zewnętrznymi dwóch wektorów. Na przykład w czterech wymiarach dwuwektor

${\ Displaystyle \ mathbf {B} = \ mathbf {e} _ {1} \ klin \ mathbf {e} _ {2} + \ mathbf {e} _ {3} \ klin \ mathbf {e} _ {4} =\mathbf {e} _{1}\mathbf {e} _{2}+\mathbf {e} _{3}\mathbf {e} _{4}=\mathbf {e} _{12}+\ matematyka {e} _{34}}$

nie można zapisać jako iloczynu zewnętrznego dwóch wektorów. Dwuwektor, który można zapisać jako iloczyn zewnętrzny dwóch wektorów, jest prosty. W dwóch i trzech wymiarach wszystkie dwuwektory są proste, ale nie w czterech lub więcej wymiarach; w czterech wymiarach każdy dwuwektor to suma najwyżej dwóch produktów zewnętrznych. Dwuwektor ma rzeczywisty kwadrat wtedy i tylko wtedy, gdy jest prosty i tylko proste dwuwektory mogą być reprezentowane geometrycznie przez zorientowany obszar płaszczyzny.

Iloczyn dwóch dwuwektorów

Iloczyn geometryczny dwóch dwuwektorów A i B wynosi

${\ Displaystyle \ mathbf {A} \ mathbf {B} = \ mathbf {A} \ cdot \ mathbf {B} + \ mathbf {A} \ razy \ mathbf {B} + \ mathbf {A} \ klin \ mathbf { B} .}$

Ilość ⋅ B jest skalar cenione wnętrza produktu, przy ∧ B jest produkt w klasie zewnętrznej 4, który pojawia się na cztery lub więcej wymiarach. Wielkość A × B jest iloczynem komutatora o wartości dwuwektorowej , podanym przez

${\ Displaystyle \ mathbf {A} \ razy \ mathbf {B} = {\ Frac {1} {2}} (\ mathbf {AB} - \ mathbf {BA})}$

Przestrzeń dwuwektorów ⋀ ² R ⁿ jest algebrą Liego nad R , z iloczynem komutatora jako nawiasem Liego. Pełny iloczyn geometryczny dwuwektorów generuje parzystą podalgebrę.

Szczególnie interesujący jest produkt dwuwektora z samym sobą. Ponieważ iloczyn komutatora jest antysymetryczny, iloczyn upraszcza się do

${\ Displaystyle \ mathbf {A} \ mathbf {A} = \ mathbf {A} \ cdot \ mathbf {A} + \ mathbf {A} \ klin \ mathbf {A}.}$

Jeśli dwuwektor jest prosty, ostatnim wyrazem jest zero, a iloczynem jest skalar o wartości A ⋅ A , który można wykorzystać do sprawdzenia prostoty. W szczególności zewnętrzny produkt dwuwektorów istnieje tylko w czterech lub więcej wymiarach, więc wszystkie dwuwektory w dwóch i trzech wymiarach są proste.

Dwa wymiary

Podczas pracy ze współrzędnymi w algebrze geometrycznej zwykle zapisuje się wektory bazowe jako ( e ₁ , e ₂ , ...), konwencja, która będzie tutaj używana.

Wektora w czasie rzeczywistym dwuwymiarowego R ² mogą być zapisywane = ₁ e ₁ + ₂ E ₂ , gdzie ₁ i ₂ są liczbami rzeczywistymi, e ₁ a e ₂ są ortonormalne wektorów bazowych. Iloczyn geometryczny dwóch takich wektorów to

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a} \ mathbf {b} i = (a_ {1} \ mathbf {e} _ {1} + a_ {2} \ mathbf {e} _ {2}) (b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2})\\&=a_{1}b_{1}\mathbf {e} _{1} \mathbf {e} _{1}+a_{1}b_{2}\mathbf {e} _{1}\mathbf {e} _{2}+a_{2}b_{1}\mathbf {e} _{2}\mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\mathbf {e} _{2}\\&=a_{1}b_{ 1}+a_{2}b_{2}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}. \end{wyrównany}}}$

Można to podzielić na symetryczny, skalarny produkt wewnętrzny i antysymetryczny, dwuwektorowy produkt zewnętrzny:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {a} \ cdot \ mathbf {b} & = a_ {1} b_ {1} + a_ {2} b_ {2}, \ \ \ mathbf {a} \ klin \mathbf {b} &=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}=(a_{1} b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{wyrównany}}}$

Wszystkie dwuwektory w dwóch wymiarach mają tę postać, czyli wielokrotności dwuwektora e ₁ e ₂ , zapisanego e ₁₂ dla podkreślenia, że ​​jest to dwuwektor, a nie wektor. Wielkość e ₁₂ wynosi 1, z

${\ Displaystyle \ mathbf {e} _ {12} ^ {2} = -1,}$

więc nazywa się to dwuwektorem jednostkowym . Termin dwuwektor jednostkowy może być używany w innych wymiarach, ale jest zdefiniowany jednoznacznie (do znaku) tylko w dwóch wymiarach, a wszystkie dwuwektory są wielokrotnościami e ₁₂ . Najwyższym elementem algebry e ₁₂ jest również pseudoskalar, któremu nadano symbol i .

Liczby zespolone

Mając własności kwadratu ujemnego i wielkości jednostkowej, dwuwektor jednostkowy może być utożsamiany z jednostką urojoną z liczb zespolonych . Dwuwektory i skalary tworzą razem parzystą podalgebrę algebry geometrycznej, która jest izomorficzna z liczbami zespolonymi C . Parzysta podalgebra ma bazę (1, e ₁₂ ), cała algebra ma bazę (1, e ₁ , e ₂ , e ₁₂ ).

Liczby zespolone są zwykle utożsamiane z osiami współrzędnych i wektorami dwuwymiarowymi, co oznaczałoby powiązanie ich z elementami wektorowymi algebry geometrycznej. Nie ma sprzeczności w tym, jak dostać się z ogólnym wektora do liczby zespolonej oś musi być zidentyfikowany jako osi rzeczywistej, e ₁ głos. To mnoży się przez wszystkie wektory, aby wygenerować elementy parzystej podalgebry.

Wszystkie własności liczb zespolonych można wyprowadzić z dwuwektorów, ale dwa są szczególnie interesujące. Po pierwsze, tak jak w przypadku liczb zespolonych iloczyny dwuwektorów, a więc podalgebry parzyste są przemienne . Odnosi się to tylko do dwóch wymiarów, więc własności dwuwektora w dwóch wymiarach, które zależą od przemienności, zwykle nie uogólniają się na wyższe wymiary.

Po drugie można zapisać ogólny dwuwektor

${\ Displaystyle \ theta \ mathbf {e} _ {12} = ja \ theta,}$

gdzie θ jest liczbą rzeczywistą. Umieszczenie tego w szereg Taylora dla przekształcenia wykładniczego i użycie własności e ₁₂ ² = −1 daje dwuwektorową wersję wzoru Eulera ,

${\ Displaystyle e ^ {\ theta \ mathbf {e} _ {12}} = e ^ {i \ theta} = \ cos {\ theta} + i \ grzech {\ teta},}$

który po pomnożeniu przez dowolny wektor obraca go o kąt θ wokół początku:

${\ Displaystyle (x '\ mathbf {e} _ {1} + Y' \ mathbf {e} _ {2}) = (x \ mathbf {e} _ {1} + r \ mathbf {e} _ {2 })e^{i\theta }.}$

Iloczyn wektora z dwuwektorem w dwóch wymiarach jest antyprzemienny , więc wszystkie poniższe iloczyny generują ten sam obrót

${\ Displaystyle \ mathbf {v} '= \ mathbf {v} e ^ {i \ theta} = e ^ {-i \ theta} \ mathbf {v} = e ^ {\ Frac {-i \ teta} {2 }}\mathbf {v} e^{\frac {i\theta }{2}}.}$

Spośród nich ostatni produkt to ten, który uogólnia się na wyższe wymiary. Potrzebna ilość nazywana jest wirnikiem i jest oznaczona symbolem R , więc w dwóch wymiarach można zapisać wirnik obracający się o kąt θ

${\ Displaystyle R = e ^ {\ Frac {-i \ theta} {2}} = e ^ {\ Frac {- \ theta \ mathbf {e} _ {12}} {2}}}$

a rotacja, którą generuje, to

${\ Displaystyle \ mathbf {v} '= R \ mathbf {v} R ^ {-1}. \,}$

Trzy wymiary

W trzech wymiarach iloczyn geometryczny dwóch wektorów to

${\displaystyle {\zacznij {wyrównany}\mathbf {ab} &=(a_{1}\mathbf {e}_{1}+a_{2}\mathbf {e}_{2}+a_{3}\ mathbf {e} _{3})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3 })\\&=a_{1}b_{1}{\mathbf {e} _{1}}^{2}+a_{2}b_{2}{\mathbf {e} _{2}}^ {2}+a_{3}b_{3}{\mathbf {e} _{3}}^{2}+(a_{2}b_{3}-a_{3}b_{2})\mathbf { e} _{2}\mathbf {e} _{3}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{3}\mathbf {e} _ {1}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}}$

Można to podzielić na symetryczny, wyceniany skalarnie, produkt wewnętrzny i antysymetryczny, wyceniany dwuwektorowo, produkt zewnętrzny:

${\displaystyle {\zacznij {wyrównany}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\ \\mathbf {a} \wedge \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{23}+(a_{3}b_ {1}-a_{1}b_{3})\mathbf {e} _{31}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12 }.\end{wyrównany}}}$

W trzech wymiarach wszystkie dwuwektory są proste, a więc są efektem produktu zewnętrznego. Dwuwektory jednostkowe e ₂₃ , e ₃₁ i e ₁₂ tworzą bazę dla przestrzeni dwuwektorów ⋀ ² R ³ , która sama jest trójwymiarową przestrzenią liniową. Więc jeśli ogólny dwuwektor to:

${\ Displaystyle \ mathbf {A} = A_ {23} \ mathbf {e} _ {23} + A_ {31} \ mathbf {e} _ {31} + A_ {12} \ mathbf {e} _ {12} ,}$

można je dodawać jak wektory

${\ Displaystyle \ mathbf {A} + \ mathbf {B} = (A_ {23} + B_ {23}) \ mathbf {e} _ {23} + (A_ {31} + B_ {31}) \ mathbf { e} _{31}+(A_{12}+B_{12})\mathbf {e} _{12}.}$

natomiast po pomnożeniu dają następujące

${\ Displaystyle \ mathbf {A} \ mathbf {B} = -A_ {23} B_ {23} -A_ {31} B_ {31} -A_ {12} B_ {12} + (A_ {12} B_ {31) }-A_{31}B_{12})\mathbf {e} _{23}+(A_{23}B_{12}-A_{12}B_{23})\mathbf {e} _{31}+ (A_{31}B_{23}-A_{23}B_{31})\mathbf {e} _{12}}$

które można podzielić na symetryczne części skalarne i antysymetryczne dwuwektorowe w następujący sposób

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {A} \ cdot \ mathbf {B} & = - A_ {12} B_ {12} -A_ {31} B_ {31} -A_ {23} B_ {23} \\\mathbf {A} \times \mathbf {B} &=(A_{23}B_{31}-A_{31}B_{23})\mathbf {e} _{12}+(A_{12} B_{23}-A_{23}B_{12})\mathbf {e} _{13}+(A_{31}B_{12}-A_{12}B_{31})\mathbf {e} _{ 23}.\end{wyrównany}}}$

Produkt zewnętrzny dwóch dwuwektorów w trzech wymiarach wynosi zero.

Dwuwektor B można zapisać jako iloczyn jego wielkości i dwuwektora jednostkowego, więc zapis β dla | B | a wykorzystując szereg Taylora do przekształcenia wykładniczego można wykazać, że

${\ Displaystyle e ^ {\ mathbf {B} } = e ^ {\ beta {\ Frac {\ mathbf {B}} {\ beta}}} = \ cos {\ beta} + {\ Frac {\ mathbf {B } }{\beta }}\sin {\beta}.}$

To kolejna wersja wzoru Eulera, ale z ogólnym dwuwektorem w trzech wymiarach. W przeciwieństwie do dwóch wymiarów dwuwymiarowe nie są przemienne, więc własności zależne od przemienności nie mają zastosowania w trzech wymiarach. Na przykład ogólnie e ^{A + B} ≠ e ^A e ^B w trzech (lub więcej) wymiarach.

Pełna algebra geometryczna w trzech wymiarach Cl ₃ ( R ) ma bazę (1, e ₁ , e ₂ , e ₃ , e ₂₃ , e ₃₁ , e ₁₂ , e ₁₂₃ ). Element e ₁₂₃ jest trójwektorem i pseudoskalarem geometrii. Dwuwektory w trzech wymiarach są czasami utożsamiane z pseudowektorami, z którymi są powiązane, co omówiono poniżej .

Kwateryny

Dwuwektory nie są zamknięte pod iloczynem geometrycznym, ale parzysta podalgebra jest. W trzech wymiarach składa się ze wszystkich elementów skalarnych i dwuwektorowych algebry geometrycznej, więc element ogólny można zapisać na przykład a + A , gdzie a jest częścią skalarną, a A jest częścią dwuwektorową. Jest napisane Cl⁺
₃i ma podstawę (1, e ₂₃ , e ₃₁ , e ₁₂ ). Iloczynem dwóch ogólnych elementów podalgebry parzystej jest

${\ Displaystyle (a + \ mathbf {A} ) (b + \ mathbf {B} ) = ab + a \ mathbf {B} + b \ mathbf {A} + \ mathbf {A} \ cdot \ mathbf {B} + \ mathbf {A} \times \mathbf {B} .}$

Podalgebra parzysta, czyli algebra składająca się ze skalarów i dwuwektorów, jest izomorficzna z kwaternionymi , H . Można to zobaczyć porównując podstawę z podstawą kwaternionów lub z powyższego produktu, który jest identyczny z produktem kwaternionów, z wyjątkiem zmiany znaku, która odnosi się do iloczynów ujemnych w iloczynie dwuwektorowym wnętrza A ⋅ B . Inne właściwości kwaternionów mogą być podobnie powiązane lub wyprowadzone z algebry geometrycznej.

Sugeruje to, że zwykły podział kwaternionów na części skalarne i wektorowe byłby lepiej reprezentowany jako podział na części skalarne i dwuwektorowe; jeśli tak się stanie, iloczyn kwaternionowy jest tylko iloczynem geometrycznym. Odnosi również kwaterniony w trzech wymiarach do liczb zespolonych w dwóch, ponieważ każda z nich jest izomorficzna z parzystą podalgebrą wymiaru, związek, który uogólnia się na wyższe wymiary.

Wektor rotacji

Wektor obrotu, z reprezentacji obrotu osiowo-kątowego , jest kompaktowym sposobem przedstawiania obrotu w trzech wymiarach. W swojej najbardziej zwartej postaci składa się z wektora, iloczynu wektora jednostkowego ω , czyli osi obrotu o kącie obrotu (ze znakiem ) θ , tak że wartość całkowitego wektora obrotu θω jest równa (bez znaku) kąt obrotu.

Kwaternion związany z rotacją to

${\ Displaystyle q = \ lewo (\ cos \ lewo ({\ Frac {\ theta} {2}} \ prawej), \ omega \ sin \ lewo ({\ Frac {\ theta} {2}} \ po prawej) \ Prawidłowy)}$

W algebrze geometrycznej obrót jest reprezentowany przez dwuwektor. Widać to w jego stosunku do kwaternionów. Niech Ω będzie dwuwektorem jednostkowym w płaszczyźnie obrotu, a θ będzie kątem obrotu . Wtedy dwuwektorem obrotu jest Ω θ . Kwaternion ściśle odpowiada wykładnikowi połowy dwuwektora Ω θ . Oznacza to, że składniki kwaternionów odpowiadają częściom skalarnym i dwuwektorowym następującego wyrażenia:

Wykładniczy można zdefiniować w kategoriach jego szeregu potęgowego i łatwo oszacować na podstawie faktu, że Ω do kwadratu wynosi -1.

Tak więc rotacje mogą być reprezentowane przez dwuwektory. Tak jak kwaterniony są elementami algebry geometrycznej, są one powiązane przez odwzorowanie wykładnicze w tej algebrze.

Wirniki

Dwuwektor Ω θ generuje obrót przez mapę wykładniczą. Wygenerowane elementy parzyste obracają wektor ogólny w trzech wymiarach w taki sam sposób jak kwaterniony:

Podobnie jak w dwóch wymiarach, wielkość e ^{- Ω θ /2} nazywana jest wirnikiem i zapisywana R . Wielkość e ^{Ω θ /2} wynosi wtedy R ⁻¹ , a generują one obroty jako

Jest to identyczne z dwoma wymiarami, z wyjątkiem tego, że wirniki są czterowymiarowymi obiektami izomorficznymi do kwaternionów. Można to uogólnić na wszystkie wymiary, z wirnikami, elementami parzystej podalgebry o jednostkowej wielkości, generowanymi przez mapę wykładniczą z dwuwektorów. Tworzą podwójną osłonę nad grupą rotacyjną, więc wirniki R i − R reprezentują ten sam obrót.

Matryce

Dwuwektory są macierzami izomorficznymi do skośnie symetrycznych ; dwuwektor ogólny B ₂₃ e ₂₃ + B ₃₁ e ₃₁ + B ₁₂ e ₁₂ mapuje do macierzy

${\ Displaystyle M_ {B} = {\ zacząć {pmatrix} 0 i B_ {12} i B_ {31} \ \-B_ {12} i 0 i B_ {23} \ \ B_ {31} i B_ {23} i 0 \ koniec {pmacierz}}.}$

To pomnożone przez wektory po obu stronach daje ten sam wektor jako iloczyn wektora i dwuwektora minus iloczyn zewnętrzny; przykładem jest tensor prędkości kątowej .

Macierze skośnie symetryczne generują macierze ortogonalne z wyznacznikiem 1 poprzez mapę wykładniczą. W szczególności wykładnik bivector związanych z obrotem jest macierz obrotu , czyli macierz obrotu M _R podane wyżej macierz antysymetryczna jest

${\ Displaystyle M_ {R} = e ^ {M_ {B}}.}$

Obrót opisany przez M _R jest taki sam, jak ten opisany przez wirnik R podany przez

${\ Displaystyle R = e ^ {\ Frac {B} {2}}}$

a macierz M _R można również obliczyć bezpośrednio z wirnika R :

${\ Displaystyle M_ {R} = {\ zacząć {pmatrix} (R \ mathbf {e} _ {1} R ^ {-1}) \ cdot \ mathbf {e} _ {1} i (R \ mathbf {e} } _{2}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _ {1}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{2}R^{- 1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{2}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e } _{3}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{3}\end{pmatrix}}.}$

Dwuwektory są powiązane z wartościami własnymi macierzy rotacji. Mając macierz rotacji M, wartości własne można obliczyć, rozwiązując równanie charakterystyczne dla tej macierzy 0 = det( M − λ I ) . Według podstawowego twierdzenia algebry ma to trzy pierwiastki (z których tylko jeden jest rzeczywisty, ponieważ istnieje tylko jeden wektor własny, tj. oś obrotu). Pozostałe korzenie muszą być złożoną parą sprzężoną. Mają jednostkę wielkości, czyli logarytmy czysto urojone, równe wielkości dwuwektora związanego z obrotem, który jest jednocześnie kątem obrotu. Wektory własne związane ze złożonymi wartościami własnymi znajdują się w płaszczyźnie dwuwektora, więc iloczyn zewnętrzny dwóch nierównoległych wektorów własnych daje w wyniku dwuwektor (lub jego wielokrotność).

Wektory osiowe

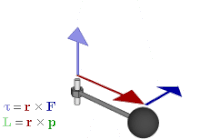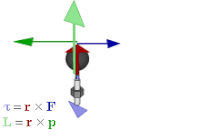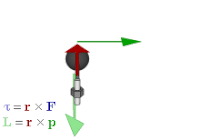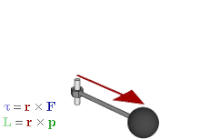
Wektor obrotu jest przykładem wektora osiowego . Wektory osiowe lub pseudowektory to wektory ze specjalną cechą polegającą na tym, że ich współrzędne ulegają zmianie znaku w stosunku do zwykłych wektorów (zwanych również „wektorami biegunowymi”) w wyniku odwrócenia przez początek, odbicie w płaszczyźnie lub inną transformację liniową odwracającą orientację . Przykładami są wielkości takie jak moment obrotowy , moment pędu i wektorowe pola magnetyczne . Wielkości, które wykorzystywałyby wektory osiowe w algebrze wektorowej są poprawnie reprezentowane przez dwuwektory w algebrze geometrycznej. Dokładniej, jeśli wybrano orientację podstawową, wektory osiowe są naturalnie identyfikowane ze zwykłymi wektorami; Hodge podwójnego otrzymuje się następnie izomorfizm między osiowymi wektorów i bivectors, więc każdy wektor osiowego związane z bivector i vice versa; to jest

${\ Displaystyle \ mathbf {A} =* \ mathbf {a} \,, \ quad \ mathbf {a} = * \ mathbf {A}}$

gdzie ∗ oznacza dual Hodge'a. Zauważ, że jeśli podstawowa orientacja jest odwrócona przez inwersję przez początek, zarówno identyfikacja wektorów osiowych ze zwykłymi wektorami, jak i znakiem podwójnej zmiany Hodge'a, ale dwuwektory się nie poruszają. Alternatywnie, używając jednostki pseudoskalarnej w Cl ₃ ( R ), i = e ₁ e ₂ e ₃ daje

${\ Displaystyle \ mathbf {A} = \ mathbf {a} ja \ , \ quad \ mathbf {a} = - \ mathbf {A} ja.}$

Jest to łatwiejsze w użyciu, ponieważ produkt jest tylko produktem geometrycznym. Jest jednak antysymetryczna, ponieważ (jak w dwóch wymiarach) jednostka pseudoskalarna i kwadrat do -1, więc w jednym z produktów potrzebna jest ujemna wartość.

Ta zależność rozciąga się na operacje takie jak iloczyn wektorowy o wartościach krzyżowych i iloczyn dwuwektorowy o wartości zewnętrznej, ponieważ zapisane jako wyznaczniki są obliczane w ten sam sposób:

${\ Displaystyle \ mathbf {a} \ razy \ mathbf {b} = {\ zacząć {vmatrix} \ mathbf {e} _ {1} i \ mathbf {e} _ {2} i \ mathbf {e} _ {3 }\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\,,\quad \mathbf {a} \wedge \mathbf { b} ={\begin{vmatrix}\mathbf {e} _{23}&\mathbf {e} _{31}&\mathbf {e} _{12}\\a_{1}&a_{2}&a_{ 3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\ ,}$

więc są spokrewnione przez Hodge'a dual:

${\ Displaystyle {* (\ mathbf {a} \ klin \ mathbf {b} )} = \ mathbf {a \ razy b} \,, \ quad {* (\ mathbf {a \ razy b} )} = \ mathbf {a} \wedge \mathbf {b} .}$

Dwuwektory mają wiele zalet w porównaniu z wektorami osiowymi. Lepiej rozróżniają wektory osiowe i biegunowe, czyli reprezentowane przez nie wielkości, dzięki czemu jest jaśniejsze, jakie operacje są dozwolone i jakie są ich wyniki. Na przykład iloczyn wewnętrzny wektora biegunowego i wektora osiowego wynikający z iloczynu poprzecznego w iloczynie potrójnym powinien dać pseudoskalar , wynik, który jest bardziej oczywisty, jeśli obliczenie jest sformułowane jako iloczyn zewnętrzny wektora i dwuwektora. Uogólniają się na inne wymiary; w szczególności dwuwektory mogą być używane do opisu wielkości takich jak moment obrotowy i moment pędu w dwóch jak i trzech wymiarach. Ponadto pod wieloma względami ściśle dopasowują się do intuicji geometrycznej, jak widać w następnej sekcji.

Interpretacja geometryczna

Jak sugeruje ich nazwa i nazwa algebry, jedną z atrakcji dwuwektorów jest to, że mają naturalną interpretację geometryczną. Można to opisać w dowolnym wymiarze, ale najlepiej jest to zrobić w trzech, gdzie można narysować paralele z bardziej znanymi obiektami, przed zastosowaniem do wyższych wymiarów. W dwóch wymiarach interpretacja geometryczna jest banalna, ponieważ przestrzeń jest dwuwymiarowa, a więc ma tylko jedną płaszczyznę, a wszystkie dwuwektory są z nią związane, różniąc się jedynie współczynnikiem skali.

Wszystkie dwuwektory można interpretować jako płaszczyzny , a dokładniej jako skierowane odcinki płaszczyzny. W trzech wymiarach istnieją trzy własności dwuwektora, które można zinterpretować geometrycznie:

• Ułożenie płaszczyzny w przestrzeni, a dokładnie położenie płaszczyzny (lub alternatywnie obrót , orientacja geometryczna lub nachylenie płaszczyzny), związane jest ze stosunkiem składowych dwuwektorowych. W szczególności trzy Podstawa bivectors, e ₂₃ , e ₃₁ i e ₁₂ , lub skalarnych wielokrotności z nich są związane z yz -plane, zx -plane i XY -plane odpowiednio.
• Wielkość z bivector wiąże się z obszaru segmentu samolotu. Obszar nie ma określonego kształtu, więc można użyć dowolnego kształtu. Można go nawet przedstawić na inne sposoby, na przykład za pomocą miary kątowej. Ale jeśli wektory są interpretowane jako długości, dwuwektor jest zwykle interpretowany jako obszar o tych samych jednostkach, w następujący sposób.
• Podobnie jak kierunek wektora, płaszczyzna powiązana z dwuwektorem ma kierunek, krążenie lub kierunek obrotu w płaszczyźnie, który przyjmuje dwie wartości widziane jako zgodne z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara , patrząc z punktu widzenia nie w płaszczyźnie. Wiąże się to ze zmianą znaku w dwuwektorze, to znaczy w przypadku odwrócenia kierunku dwuwektor zostaje zanegowany. Alternatywnie, jeśli dwa dwuwektory mają tę samą postawę i wielkość, ale przeciwne kierunki, to jeden jest negatywem drugiego.
• Jeśli wyobrazimy sobie jako równoległobok, z początkiem wektorów na 0, to obszar ze znakiem jest wyznacznikiem współrzędnych kartezjańskich wektorów ( a _x b _y − b _x a _y ).

W trzech wymiarach wszystkie dwuwektory mogą być generowane przez iloczyn zewnętrzny dwóch wektorów. Jeśli dwuwektor B = a ∧ b to wielkość B wynosi

${\ Displaystyle \ lewo | \ mathbf {B} \ prawo | = \ lewo | \ mathbf {a} \ prawo | \ lewo | \ mathbf {b} \ prawo | \ grzech {\ theta}}$

gdzie θ jest kątem między wektorami. Jest to obszar równoległoboku z krawędziami a i b , jak pokazano na diagramie. Jedna z interpretacji jest taka, że ​​obszar jest wymiatany przez b, gdy porusza się wzdłuż a . Produkt zewnątrz jest antysymetryczna, to odwrócenie kolejności i B , aby w ruch wzdłuż b wyników w bivector do kierunku przeciwnym jest ujemny w stosunku do pierwszego. Płaszczyzna dwuwektora a ∧ b zawiera zarówno a, jak i b, więc oba są równoległe do płaszczyzny.

Dwuwektory i wektory osiowe są powiązane przez Hodge dual . W rzeczywistej przestrzeni wektorowej Hodge dual odnosi podprzestrzeń do jej dopełnienia ortogonalnego , więc jeśli dwuwektor jest reprezentowany przez płaszczyznę, to wektor osiowy z nim związany jest po prostu normalną do powierzchni tej płaszczyzny . Płaszczyzna ma dwie normalne, po jednej z każdej strony, co daje dwie możliwe orientacje płaszczyzny i dwuwektora.

Odnosi się przekrój produkt do wyrobu zewnętrznych . Może być również używany do reprezentowania wielkości fizycznych, takich jak moment obrotowy i moment pędu . W algebrze wektorowej są one zwykle reprezentowane przez wektory prostopadłe do płaszczyzny siły , pędu liniowego lub przemieszczenia, z których są obliczane. Ale jeśli zamiast tego używany jest dwuwektor, płaszczyzna jest płaszczyzną dwuwektora, więc jest to bardziej naturalny sposób przedstawiania wielkości i sposobu ich działania. Również w przeciwieństwie do reprezentacji wektorowej uogólnia się na inne wymiary.

Iloczyn dwóch dwuwektorów ma interpretację geometryczną. Dla niezerowych dwuwektorów A i B iloczyn można podzielić na części symetryczne i antysymetryczne w następujący sposób:

${\ Displaystyle \ mathbf {AB} = \ mathbf {A} \ cdot \ mathbf {B} + \ mathbf {A} \ razy \ mathbf {B}.}$

Podobnie jak wektory, mają one wielkości | A ⋅ B | = | | | B | cos θ i | A × B | = | | | B | sin θ , gdzie θ jest kątem między płaszczyznami. W trzech wymiarach jest taki sam, jak kąt między wektorami normalnymi dualnymi do płaszczyzn, i uogólnia się do pewnego stopnia w wyższych wymiarach.

Dwuwektory można dodawać razem jako obszary. Biorąc pod uwagę dwie niezerowe bivectors B i C w trzech wymiarach jest to zawsze możliwe, aby znaleźć wektor, który jest zawarty w obu, do powiedzenia, więc bivectors można zapisać jako produkty zewnętrznych związanych :

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {B} & = \ mathbf {a} \ klin \ mathbf {b} \ \ \ mathbf {C} & = \ mathbf {a} \ klin \ mathbf {c} \ koniec{wyrównany}}}$

Można to zinterpretować geometrycznie, jak widać na diagramie: dwa obszary sumują się, dając trzecią, przy czym trzy obszary tworzą ściany pryzmatu z a , b , c i b + c jako krawędziami. Odpowiada to dwóm sposobom obliczania powierzchni przy użyciu rozdzielności produktu zewnętrznego:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {B} + \ mathbf {C} & = \ mathbf {a} \ klin \ mathbf {b} + \ mathbf {a} \ klin \ mathbf {c} \ \ & =\mathbf {a} \wedge (\mathbf {b} +\mathbf {c} ).\end{wyrównany}}}$

Działa to tylko w trzech wymiarach, ponieważ jest to jedyny wymiar, w którym musi istnieć wektor równoległy do ​​obu dwuwektorów. W wyższych wymiarach dwuwektory na ogół nie są związane z jedną płaszczyzną, a jeśli są (proste dwuwektory), dwa dwuwektory mogą nie mieć wspólnego wektora, a więc sumują się do nieprostego dwuwektora.

Cztery wymiary

W czterech wymiarach bazowymi elementami przestrzeni ⋀ ² R ⁴ dwuwektorów są ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ), więc ogólny dwuwektor ma postać

${\ Displaystyle \ mathbf {A} = a_ {12} \ mathbf {e} _ {12} + a_ {13} \ mathbf {e} _ {13} + a_ {14} \ mathbf {e} _ {14} +a_{23}\mathbf {e} _{23}+a_{24}\mathbf {e} _{24}+a_{34}\mathbf {e} _{34}.}$

Ortogonalność

W czterech wymiarach podwójny Hodge'a dwuwektora jest dwuwektorem, a przestrzeń ⋀ ² R ⁴ jest do siebie podwójna. Wektory normalne nie są unikalne, zamiast tego każda płaszczyzna jest ortogonalna do wszystkich wektorów w swojej przestrzeni podwójnej Hodge'a. Można to wykorzystać do podzielenia dwuwektorów na dwie „połówki” w następujący sposób. Mamy trzy pary dwuwektorów ortogonalnych: ( e ₁₂ , e ₃₄ ), ( e ₁₃ , e ₂₄ ) i ( e ₁₄ , e ₂₃ ). Istnieją cztery różne sposoby wybrania jednego dwuwektora z każdej z pierwszych dwóch par, a po wybraniu tych dwóch pierwszych ich suma daje trzeci dwuwektor z drugiej pary. Na przykład, ( e ₁₂ , e ₁₃ , e ₁₄ ) i ( E ₂₃ , E ₂₄ , e ₃₄ ).

Proste dwuwektory w 4D

W czterech wymiarach dwuwektory są generowane przez iloczyn zewnętrzny wektorów w R ⁴ , ale z jedną istotną różnicą w stosunku do R ³ i R ² . W czterech wymiarach nie wszystkie dwuwektory są proste. Istnieje bivectors takich jak e ₁₂ + E ₃₄ , które nie mogą być generowane przez zewnętrzne dwóch wektorów. Oznacza to również, że nie mają rzeczywistego, czyli skalarnego, kwadratu. W tym przypadku

${\ Displaystyle (\ mathbf {e} _ {12} + \ mathbf {e} _ {34}) ^ {2} = \ mathbf {e} _ {12} \ mathbf {e} _ {12} + \ mathbf {e} _{12}\mathbf {e} _{34}+\mathbf {e} _{34}\mathbf {e} _{12}+\mathbf {e} _{34}\mathbf {e} _{34}=-2+2\mathbf {e} _{1234}.}$

Element e ₁₂₃₄ jest pseudoskalarem w Cl ₄ , różnym od skalara, więc kwadrat jest nieskalarny.

Wszystkie dwuwektory w czterech wymiarach można wygenerować przy użyciu maksymalnie dwóch produktów zewnętrznych i czterech wektorów. Powyższy dwuwektor można zapisać jako

${\ Displaystyle \ mathbf {e} _ {12} + \ mathbf {e} _ {34} = \ mathbf {e} _ {1} \ klin \ mathbf {e} _ {2} + \ mathbf {e} _ {3}\wedge \mathbf {e} _{4}.}$

Podobnie każdy dwuwektor można zapisać jako sumę dwóch prostych dwuwektorów. W tym celu warto wybrać dwa dwuwektory ortogonalne i zawsze jest to możliwe. Co więcej, w przypadku dwuwektora generycznego wybór prostych dwuwektorów jest unikalny, co oznacza, że ​​istnieje tylko jeden sposób rozkładu na dwuwektory ortogonalne; jedynym wyjątkiem jest sytuacja, gdy dwa ortogonalne dwuwektory mają równe wielkości (jak w powyższym przykładzie): w tym przypadku rozkład nie jest niepowtarzalny. Rozkład jest zawsze wyjątkowy w przypadku prostych dwuwektorów, z dodatkową premią, że jedna z części ortogonalnych wynosi zero.

Obroty w R ⁴

Tak jak w trójwymiarze dwuwektory w czterowymiarze generują rotacje poprzez mapę wykładniczą i wszystkie rotacje mogą być generowane w ten sposób. Podobnie jak w trzech wymiarach, jeśli B jest dwuwektorem, to wirnik R jest e ^{B /2} i obroty są generowane w ten sam sposób:

${\ Displaystyle v '= RvR ^ {-1}. \,}$

Generowane rotacje są jednak bardziej złożone. Można je podzielić na następujące kategorie:

proste obroty to takie, które ustalają płaszczyznę w 4D i obracają się o kąt „wokół” tej płaszczyzny.

podwójne obroty mają tylko jeden stały punkt, początek i obracają się o dwa kąty wokół dwóch prostopadłych płaszczyzn. Ogólnie kąty są różne, a płaszczyzny są jednoznacznie określone

rotacje izokliniczne są rotacjami podwójnymi, w których kąty obrotu są równe. W tym przypadku płaszczyzny, wokół których następuje rotacja, nie są unikalne.

Są one generowane przez dwuwektory w prosty sposób. Proste rotacje są generowane przez proste dwuwektory, przy czym stała płaszczyzna jest podwójna lub prostopadła do płaszczyzny dwuwektora. Można powiedzieć, że obrót odbywa się wokół tej płaszczyzny, w płaszczyźnie dwuwektora. Wszystkie inne dwuwektory generują podwójne rotacje, przy czym dwa kąty obrotu są równe wielkościom dwóch prostych dwuwektorów, z których składa się dwuwektor nieprosty. Rotacje izokliniczne powstają, gdy te wielkości są równe, w którym to przypadku rozkład na dwa proste dwuwektory nie jest wyjątkowy.

Dwuwektory na ogół nie dojeżdżają, ale jednym wyjątkiem są dwuwektory ortogonalne i ich wykładniki. Więc jeśli dwuwektor B = B ₁ + B ₂ , gdzie B ₁ i B ₂ są prostopadłymi prostymi dwuwektorami, jest używany do wygenerowania rotacji, rozkłada się na dwa proste rotacje, które przechodzą w następujący sposób:

${\ Displaystyle R = e ^ {\ Frac {\ mathbf {B} _ {1} + \ mathbf {B} _ {2}} {2}} = e ^ {\ Frac {\ mathbf {B} _ {1 }}{2}}e^{\frac {\mathbf {B} _{2}}{2}}=e^{\frac {\mathbf {B} _{2}}{2}}e^{ \frac {\mathbf {B} _{1}}{2}}}$

Zawsze jest to możliwe, ponieważ wszystkie dwuwektory można wyrazić jako sumy dwuwektorów ortogonalnych.

Rotacje czasoprzestrzeni

Czasoprzestrzeń to matematyczny model naszego wszechświata, używany w szczególnej teorii względności. Składa się z trzech wymiarów przestrzennych i jednego wymiaru czasowego połączonych w pojedynczą czterowymiarową przestrzeń. Opisuje się ją naturalnie za pomocą algebry geometrycznej i dwuwektorów, przy czym metryka euklidesowa została zastąpiona metryką Minkowskiego . Ta algebra jest identyczna z algebrą przestrzeni euklidesowej, z wyjątkiem zmiany sygnatury , więc

${\ Displaystyle {\ mathbf {e} _ {i}} ^ {2} = {\ zacząć {przypadki} 1, i i = 1,2, 3 \ \ 1, & i = 4 \ koniec {przypadki}}}$

(Zauważ, że kolejność i indeksy powyżej nie są uniwersalne – tutaj e ₄ jest wymiarem czasopodobnym). Algebra geometryczna to Cl _3,1 ( R ), a podprzestrzeń dwuwektorów to ⋀ ² R ^3,1 .

Proste dwuwektory są dwojakiego rodzaju. Proste dwuwektory e ₂₃ , e ₃₁ i e ₁₂ mają ujemne kwadraty i obejmują dwuwektory trójwymiarowej podprzestrzeni odpowiadającej przestrzeni euklidesowej R ³ . Te dwuwektory generują zwykłe rotacje w R ³ .

Proste bivectors e ₁₄ , e ₂₄ i E ₃₄ ma dodatnie pola jak i płaszczyzny obejmują wymiaru przestrzeni i do wymiaru czasu. Generują one również obroty na mapie wykładniczej, ale zamiast funkcji trygonometrycznych potrzebne są funkcje hiperboliczne, które generują wirnik w następujący sposób:

${\ Displaystyle e ^ {\ Frac {{\ boldsymbol {\ Omega}} \ theta} {2}} = \ cosh \ lewo ({\ Frac {\ theta} {2}} \ po prawej) + {\ boldsymbol {\ Omega }}\sinh \left({\frac {\theta }{2}}\right),}$

gdzie Ω jest dwuwektorem ( e ₁₄ itd.), identyfikowanym za pomocą metryki z antysymetryczną transformacją liniową R ^3,1 . Są to wzmocnienia Lorentza , wyrażone w szczególnie zwarty sposób, przy użyciu tego samego rodzaju algebry, co w R ³ i R ⁴ .

Ogólnie wszystkie rotacje czasoprzestrzeni są generowane z dwuwektorów poprzez mapę wykładniczą, czyli ogólny wirnik generowany przez dwuwektor A ma postać

${\ Displaystyle R = e ^ {\ Frac {\ mathbf {A} } {2}}.}$

Zbiór wszystkich rotacji w czasoprzestrzeni z grupy Lorentza i z nich można wydedukować większość konsekwencji szczególnej teorii względności. Bardziej ogólnie pokazuje to, jak transformacje w przestrzeni euklidesowej i czasoprzestrzeni można opisać za pomocą tego samego rodzaju algebry.

równania Maxwella

(Uwaga: w tej sekcji tradycyjne trójwektory są oznaczone liniami nad symbolami, a wektor czasoprzestrzeni i dwuwektory pogrubionymi symbolami, przy czym wektory J i A są wyjątkowo pisane wielkimi literami)

Równania Maxwella są używane w fizyce do opisu relacji między polami elektrycznymi i magnetycznymi . Zwykle podane jako cztery równania różniczkowe mają szczególnie zwartą postać, gdy pola są wyrażone jako dwuwektor czasoprzestrzenny z ⋀ ² R ^3,1 . Jeśli pola elektryczne i magnetyczne w R ³ to E i B, to dwuwektor elektromagnetyczny to

${\ Displaystyle \ mathbf {F} = {\ Frac {1} {c}} {\ overline {E}} \ mathbf {e} _ {4}+ {\ overline {B}} \ mathbf {e} _ { 123},}$

gdzie e ₄ jest znowu wektorem bazowym wymiaru czasopodobnego, a c jest prędkością światła . Iloczyn B e ₁₂₃ daje dwuwektor, który jest dualny Hodge'a do B w trzech wymiarach, jak omówiono powyżej , podczas gdy E e ₄ jako iloczyn wektorów ortogonalnych ma również wartość dwuwektorową. Jako całość jest to tensor elektromagnetyczny wyrażony bardziej zwięźle jako dwuwektor i jest używany w następujący sposób. Najpierw jest powiązany z 4-prądowym J , wielkością wektorową podaną przez

${\ Displaystyle \ mathbf {J} = {\ overline {j}} + c \ rho \ mathbf {e} _ {4}}$

gdzie j jest gęstością prądu, a ρ jest gęstością ładunku . Są one powiązane operatorem różniczkowym ∂, którym jest

${\ Displaystyle \ częściowy = \ nabla - \ mathbf {e} _ {4} {\ Frac {1} {c}} {\ Frac {\ częściowy} {\ częściowy t}}.}$

Operator ∇ jest operatorem różniczkowym w algebrze geometrycznej, działającym na wymiarach przestrzeni i podanym przez ∇ M = ∇⋅ M + ∇∧ M . Gdy stosuje się wektory ∇⋅ M jest rozbieżność i ∇∧ M jest zwijanie ale z bivector niż rezultacie wektor, który ma podwójne w trzech wymiarach do zawinięcia. Dla ogólnej wielkości M działają one jako operatory różniczkowe obniżające i podnoszące. W szczególności, jeśli M jest skalarem, to ten operator jest po prostu gradientem i można go traktować jako geometryczny operator algebraiczny del .

Razem można je wykorzystać do uzyskania szczególnie zwartej formy równań Maxwella ze źródłami:

${\ Displaystyle \ częściowy \ mathbf {F} = \ mathbf {J}.}$

To równanie, po rozłożeniu zgodnie z algebrą geometryczną, przy użyciu iloczynów geometrycznych, które mają zarówno efekt podnoszenia, jak i obniżania oceny, jest równoważne czterem równaniom Maxwella. Jest to również związane z czteropotencjałem elektromagnetycznym , wektorem A podanym przez

${\ Displaystyle \ mathbf {A} = {\ overline {A}} + {\ Frac {1} {c}} V \ mathbf {e} _ {4}}$

gdzie A jest wektorem potencjału magnetycznego, a V jest potencjałem elektrycznym. Jest to związane z dwuwektorem elektromagnetycznym w następujący sposób

${\ Displaystyle \ częściowy \ mathbf {A} =- \ mathbf {F},}$

używając tego samego operatora różniczkowego ∂.

Wyższe wymiary

Jak sugerowano we wcześniejszych rozdziałach, wiele algebr geometrycznych dobrze uogólnia się na wyższe wymiary. Algebra geometryczna dla przestrzeni rzeczywistej R ⁿ to Cl _n ( R ), a podprzestrzeń dwuwektorów to ⋀ ² R ⁿ .

Liczba prostych dwuwektorów potrzebnych do utworzenia ogólnego dwuwektora rośnie wraz z wymiarem, więc dla n nieparzystych jest to ( n − 1) / 2 , dla n parzyste jest to n / 2 . Tak więc dla czterech i pięciu wymiarów potrzebne są tylko dwa proste dwuwektory, ale trzy są wymagane dla sześciu i siedmiu wymiarów. Na przykład w sześciu wymiarach ze standardową podstawą ( e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ ) dwuwektor

${\ Displaystyle \ mathbf {e} _ {12} + \ mathbf {e} _ {34} + \ mathbf {e} _ {56}}$

to suma trzech prostych dwuwektorów, ale nie mniej. Tak jak w czterech wymiarach, dla tej sumy zawsze można znaleźć proste dwuwektory ortogonalne.

Obroty w wyższych wymiarach

Ponieważ w trzech i czterech wymiarach wirniki są generowane przez mapę wykładniczą, więc

${\ Displaystyle e ^ {\ Frac {\ mathbf {B} } {2}}}$

to wirnik generowany przez dwuwektor B . Obroty proste, które odbywają się w płaszczyźnie obrotu wokół stałej łopatki o wymiarze ( n − 2), generowane są przez proste dwuwektory, podczas gdy pozostałe dwuwektory generują bardziej złożone rotacje, które można opisać w kategoriach prostych dwuwektorów, których są sumami, każdy związany z płaszczyzną obrotu. Wszystkie dwuwektory można wyrazić jako sumę prostych dwuwektorów ortogonalnych i przemiennych, więc rotacje można zawsze rozłożyć na zbiór obrotów przemiennych wokół płaszczyzn powiązanych z tymi dwuwektorami. Grupa wirników w n wymiarach to grupa spinowa Spin( n ).

Godną uwagi cechą, związaną z liczbą prostych dwuwektorów, a więc płaszczyzn obrotu, jest to, że w nieparzystych wymiarach każdy obrót ma stałą oś – mylące jest nazywanie tego osią obrotu, ponieważ w wyższych wymiarach obrót odbywa się w wielu płaszczyznach ortogonalnych do niego. Jest to związane z dwuwektorami, ponieważ dwuwektory w nieparzystych wymiarach rozkładają się na taką samą liczbę dwuwektorów, jak w parzystym wymiarze poniżej, więc mają taką samą liczbę płaszczyzn, ale jeden dodatkowy wymiar. Ponieważ każda płaszczyzna generuje obroty w dwóch wymiarach w nieparzystych wymiarach, musi istnieć jeden wymiar, czyli oś, która nie jest obracana.

Dwuwektory są również powiązane z macierzą rotacji w n wymiarach. Podobnie jak w trzech wymiarach, równanie charakterystyczne macierzy można rozwiązać, aby znaleźć wartości własne . W nieparzystych wymiarach ma jeden prawdziwy pierwiastek, z wektorem własnym stałą oś, aw parzystych wymiarach nie ma prawdziwych pierwiastków, więc albo wszystkie albo wszystkie oprócz jednego z pierwiastków są złożonymi parami sprzężonymi. Każda para jest powiązana z prostym składnikiem dwuwektora związanego z obrotem. W szczególności logarytm każdej pary wynosi ± wielkość, podczas gdy wektory własne generowane z korzeni są równoległe do dwuwektora i mogą być użyte do wygenerowania dwuwektora. Ogólnie wartości własne i dwuwektory są unikalne, a zbiór wartości własnych daje pełny rozkład na proste dwuwektory; jeśli korzenie się powtarzają, to rozkład dwuwektora na proste dwuwektory nie jest wyjątkowy.

Geometria rzutowa

Algebrę geometryczną można zastosować do geometrii rzutowej w prosty sposób. Zastosowana algebra geometryczna to Cl _n ( R ), n ≥ 3 , algebra rzeczywistej przestrzeni wektorowej R ⁿ . Służy do opisu obiektów w rzeczywistej przestrzeni rzutowej RP ^{n −1} . Niezerowe wektory w Cl _n ( R ) lub R ⁿ są powiązane z punktami w przestrzeni rzutowej, więc wektory, które różnią się tylko współczynnikiem skali, więc ich iloczyn zewnętrzny wynosi zero, mapują się do tego samego punktu. Niezerowe dwuwektory proste w ⋀ ² R ⁿ reprezentują linie w RP ^{n -1} , przy czym dwuwektory różnią się tylko (dodatnim lub ujemnym) współczynnikiem skali reprezentującym tę samą linię.

Opis geometrii rzutowej można skonstruować w algebrze geometrycznej za pomocą podstawowych operacji. Na przykład, biorąc pod uwagę dwie odrębne punkty RP ^{n -1} reprezentowane przez wektory i b linii zawierających je podaje się w ∧ b (lub b ∧ ). Dwie proste przecinają się w punkcie, jeśli A ∧ B = 0 dla ich dwuwektorów A i B . Ten punkt jest podany przez wektor

${\ Displaystyle \ mathbf {p} = \ mathbf {A} \ Lor \ mathbf {B} = (\ mathbf {A} \ razy \ mathbf {B}) J ^ {-1}.}$

Operacja "∨" jest spotkaniem, które można zdefiniować jak powyżej w odniesieniu do złączenia, J = A ∧ B dla niezerowego A ∧ B . Korzystając z tych operacji, geometrię rzutową można sformułować w kategoriach algebry geometrycznej. Na przykład, mając trzeci (niezerowy) dwuwektor C, punkt p leży na prostej podanej przez C wtedy i tylko wtedy, gdy

${\ Displaystyle \ mathbf {p} \ ziemia \ mathbf {C} = 0.}$

Zatem warunkiem współliniowości linii podanych przez A , B i C jest

${\ Displaystyle (\ mathbf {A} \ Lor \ mathbf {B} ) \ ziemi \ mathbf {C} = 0}$

co w Cl ₃ ( R ) i RP ² upraszcza się do

${\ Displaystyle \ langle \ mathbf {ABC} \ rangle = 0}$

gdzie nawiasy kątowe oznaczają skalarną część iloczynu geometrycznego. W ten sam sposób wszystkie operacje w przestrzeni rzutowej można zapisać w kategoriach algebry geometrycznej, z dwuwektorami reprezentującymi linie ogólne w przestrzeni rzutowej, tak więc całą geometrię można opracować za pomocą algebry geometrycznej.

Tensory i macierze

Jak wspomniano powyżej, dwuwektor można zapisać jako macierz skośno-symetryczną, która poprzez mapę wykładniczą generuje macierz rotacji opisującą ten sam obrót co wirnik, również generowaną przez mapę wykładniczą, ale zastosowaną do wektora. Ale jest również używany z innymi dwuwektorami, takimi jak tensor prędkości kątowej i tensor elektromagnetyczny , odpowiednio macierz skośno-symetryczna 3×3 i 4×4 lub tensor.

Dwuwektory rzeczywiste w ⋀ ² R ⁿ są izomorficzne z macierzami skośnie symetrycznymi n × n lub alternatywnie z antysymetrycznymi tensorami stopnia 2 na R ⁿ . Chociaż dwuwektory są izomorficzne z wektorami (poprzez dualność) w trzech wymiarach, mogą być reprezentowane przez macierze skośno-symetryczne w dowolnym wymiarze. Jest to przydatne do powiązania dwuwektorów z problemami opisywanymi przez macierze, dzięki czemu można je ponownie rzutować na dwuwektory, mając interpretację geometryczną, a następnie często łatwiej rozwiązywać lub powiązać geometrycznie z innymi problemami dwuwektorowymi.

Mówiąc bardziej ogólnie, każda rzeczywista algebra geometryczna jest izomorficzna z algebrą macierzową . Zawierają one dwuwektory jako podprzestrzeń, choć często w sposób mało użyteczny. Macierze te są głównie interesujące jako sposób klasyfikacji algebr Clifforda.

Zobacz też

• Wielowektorowy
• Algebra wieloliniowa

Uwagi

Ogólne odniesienia

• Lew Dorst; Daniela Fontijne'a; Stephena Manna (2009). „§ 2.3.3 Wizualizacja dwuwektorów” . Algebra geometryczna dla informatyki: obiektowe podejście do geometrii (2nd ed.). Morgana Kaufmanna. P. 31 i następne . Numer ISBN 978-0-12-374942-0.
• Whitney, Hassler (1957). Teoria integracji geometrycznej . Princeton: Wydawnictwo Uniwersytetu Princeton . Numer ISBN 978-0-486-44583-0.

• Lounesto, Pertti (2001). Algebry i spinory Clifforda . Cambridge: Wydawnictwo Uniwersytetu Cambridge . Numer ISBN 978-0-521-00551-7.

• Chrisa Dorana i Anthony'ego Lasenby'ego (2003). „§ 1.6 Produkt zewnętrzny” . Algebra geometryczna dla fizyków . Cambridge: Wydawnictwo Uniwersytetu Cambridge . P. 11 i nast . Numer ISBN 978-0-521-71595-9.