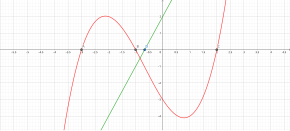
Twierdzenie Rolle'a - Rolle's theorem
| Część serii artykułów o |
| Rachunek różniczkowy |
|---|

W rachunku , twierdzenie rolle'a lub lemat Rolle w zasadzie stanowi, że każdy rzeczywista różniczkowalną funkcją że osiąga takie same wartości w dwóch różnych punktach musi mieć co najmniej jeden stacjonarny punkt gdzieś między nimi, to jest punkt, w którym pierwsza pochodna (nachylenie styczna do wykresu funkcji) wynosi zero. Twierdzenie nosi imię Michela Rolle'a .
Standardowa wersja twierdzenia
W przypadku rzeczywistego -valued funkcja f jest ciągłą w odpowiednim przedziale zamkniętym [ , b ] , różniczkowalną w przedziale otwartym ( , b ) i f ( ) = f ( b ) , po czym istnieje co najmniej jeden c w przedział otwarty ( a , b ) taki, że
- .
Ta wersja twierdzenia Rolle'a służy do udowodnienia twierdzenia o wartości średniej , którego twierdzenie Rolle'a jest rzeczywiście przypadkiem szczególnym. Jest to również podstawa dowodu twierdzenia Taylora .
Historia
Chociaż twierdzenie nosi imię Michela Rolle'a , dowód Rolle'a z 1691 r. obejmował tylko przypadek funkcji wielomianowych. Jego dowód nie wykorzystywał metod rachunku różniczkowego , które w tamtym momencie swojego życia uważał za błędne. Twierdzenie to zostało po raz pierwszy udowodnione przez Cauchy'ego w 1823 jako następstwo dowodu twierdzenia o wartości średniej . Nazwa „Twierdzenie Rolle'a” została po raz pierwszy użyta przez Moritza Wilhelma Drobischa z Niemiec w 1834 roku i przez Giusto Bellavitisa z Włoch w 1846 roku.
Przykłady
Pierwszy przykład
Dla promienia r > 0 rozważ funkcję
Jego wykres to górny półokrąg wyśrodkowany na początku. Funkcja ta jest ciągła na przedział zamkniętą [- r , R ] i różniczkowalną w przedziale otwartym (- r , r ) , ale nie różniczkowalną w końcowych - R i R . Ponieważ f (− r ) = f ( r ) , twierdzenie Rolle'a ma zastosowanie i rzeczywiście istnieje punkt, w którym pochodna f wynosi zero. Zauważ, że twierdzenie ma zastosowanie nawet wtedy, gdy funkcja nie może być zróżnicowana w punktach końcowych, ponieważ wymaga tylko, aby funkcja była różniczkowalna w otwartym przedziale.
Drugi przykład
Jeżeli różniczkowalność nie powiedzie się w wewnętrznym punkcie przedziału, wniosek z twierdzenia Rolle'a może się nie sprawdzić. Rozważ funkcję wartości bezwzględnej
Wtedy f (−1) = f (1) , ale nie ma c między -1 a 1, dla którego f ′( c ) wynosi zero. Dzieje się tak, ponieważ ta funkcja, chociaż ciągła, nie jest różniczkowalna przy x = 0 . Zauważ, że pochodna f zmienia swój znak przy x = 0 , ale bez osiągnięcia wartości 0. Twierdzenia nie można zastosować do tej funkcji, ponieważ nie spełnia warunku, że funkcja musi być różniczkowalna dla każdego x w przedziale otwartym. Jednakże, gdy wymóg różniczkowalności zostanie usunięty z twierdzenia Rolle'a, f nadal będzie miało krytyczną liczbę w otwartym przedziale ( a , b ) , ale może nie dać tangensa poziomego (jak w przypadku wartości bezwzględnej przedstawionej na wykresie ).
Uogólnienie
Drugi przykład ilustruje następujące uogólnienie twierdzenia Rolle'a:
Rozważmy funkcję ciągłą o wartościach rzeczywistych f na przedziale domkniętym [ a , b ] z f ( a ) = f ( b ) . Jeśli dla każdego x w otwartym przedziale ( a , b ) granica po prawej stronie
i limit lewej ręki
istnieją w rozszerzonej prostej rzeczywistej [−∞, ∞] , to istnieje pewna liczba c w otwartym przedziale ( a , b ) taka, że jedna z dwóch granic
jest ≥ 0, a druga ≤ 0 (w rozszerzonej linii rzeczywistej). Jeśli granice prawo- i lewostronne zgadzają się dla każdego x , to zgadzają się w szczególności dla c , stąd pochodna f istnieje w c i jest równa zeru.
Uwagi
- Jeśli f jest wypukłe lub wklęsłe, to pochodne prawo- i lewoskrętne istnieją w każdym punkcie wewnętrznym, stąd powyższe granice istnieją i są liczbami rzeczywistymi.
- Ta uogólniona wersja twierdzenia wystarcza do udowodnienia wypukłości, gdy pochodne jednostronne rosną monotonicznie :
Dowód wersji uogólnionej
Ponieważ dowód dla standardowej wersji twierdzenia Rolle'a i uogólnienie są bardzo podobne, dowodzimy uogólnienia.
Idea dowodu dowodzić, że jeśli f ( ) = f ( b ) , a następnie f musi osiągnąć albo maksymalną lub minimalną gdzieś pomiędzy i B , przykładowo co c , a funkcja może zmieniać przed wzrostem do zmniejszania ( lub odwrotnie) w c . W szczególności, jeśli pochodna istnieje, musi wynosić zero w c .
Z założenia, f jest ciągłe na [ a , b ] , a twierdzenie o wartości ekstremalnej osiąga zarówno maksimum jak i minimum w [ a , b ] . Jeśli oba są osiągnięte w punktach końcowych [ a , b ] , to f jest stałe w [ a , b ] , a więc pochodna f wynosi zero w każdym punkcie w ( a , b ) .
Przyjmijmy wówczas, że maksymalna uzyskuje się przy wewnętrznym punkcie C o ( , b ) (argument do minimum jest bardzo podobne, to pod uwagę - F ). Powyższe granice prawej i lewej strony zbadamy osobno.
Dla rzeczywistego h takiego , że c + h jest w [ a , b ] , wartość f ( c + h ) jest mniejsza lub równa f ( c ) , ponieważ f osiąga maksimum w c . Dlatego dla każdego h > 0 ,
W związku z tym
gdzie granica istnieje z założenia, może wynosić minus nieskończoność.
Podobnie, dla każdego h < 0 nierówność się odwraca, ponieważ mianownik jest teraz ujemny i otrzymujemy
W związku z tym
gdzie granica może być plus nieskończoność.
Wreszcie, gdy powyższe granice prawej i lewej strony zgadzają się (w szczególności, gdy f jest różniczkowalne), to pochodna f w c musi wynosić zero.
(Alternatywnie możemy bezpośrednio zastosować twierdzenie Fermata o punkcie stacjonarnym ).
Uogólnienie na wyższe pochodne
Możemy również uogólnić twierdzenie Rolle'a, wymagając, aby f miało więcej punktów o równych wartościach i większej regularności. Załóżmy, że…
- funkcja f jest n − 1 razy różniczkowalna w sposób ciągły na przedziale domkniętym [ a , b ] a n- ta pochodna istnieje na przedziale otwartym ( a , b ) , oraz
- istnieje n przedziałów podanych przez a 1 < b 1 ≤ a 2 < b 2 ≤ … ≤ a n < b n w [ a , b ] takie, że f ( a k ) = f ( b k ) dla każdego k od 1 do n .
Wtedy istnieje liczba c w ( a , b ) taka, że n- ta pochodna f w c wynosi zero.
Wymagania dotyczące n- tej pochodnej f można osłabić, jak w powyższym uogólnieniu, podając odpowiednie (być może słabsze) twierdzenia dla prawych i lewych granic zdefiniowanych powyżej z f ( n − 1) zamiast f .
W szczególności ta wersja twierdzenia zakłada, że jeśli funkcja wystarczająco różniczkowalna ma n pierwiastków (a więc mają tę samą wartość, czyli 0), to istnieje wewnętrzny punkt, w którym f ( n − 1) znika.
Dowód
Dowód wykorzystuje indukcję matematyczną . Przypadek n = 1 jest po prostu standardową wersją twierdzenia Rolle'a. Dla n > 1 przyjmij hipotezę indukcyjną, że uogólnienie jest prawdziwe dla n − 1 . Chcemy to udowodnić dla n . Załóżmy, że funkcja f spełnia hipotezy twierdzenia. Przy standardowym tw Rolka jest dla każdej liczby całkowitej K od 1 do n , istnieje c, k na wolnym odstępie ( a k , b k ) , tak że F "( C k ) = 0 . Zatem pierwsza pochodna spełnia założenia na n − 1 przedziałach domkniętych [ c 1 , c 2 ], …, [ c n − 1 , c n ] . Zgodnie z hipotezą indukcyjną istnieje c takie, że ( n − 1) pierwsza pochodna f ′ w c wynosi zero.
Uogólnienia na inne dziedziny
Twierdzenie Rolle'a jest własnością funkcji różniczkowalnych nad liczbami rzeczywistymi, które są polem uporządkowanym . Jako taki, nie uogólnia na inne pola , ale następujący wniosek tak: jeśli wielomian rzeczywisty (ma wszystkie swoje pierwiastki) po liczbach rzeczywistych, to jego pochodna również. Tę właściwość można nazwać właściwością pola Własność Rolle'a . Pola bardziej ogólne nie zawsze mają funkcje różniczkowalne, ale zawsze mają wielomiany, które można różnicować symbolicznie. Podobnie, bardziej ogólne pola mogą nie mieć porządku, ale istnieje pojęcie pierwiastka wielomianu leżącego w polu.
Zatem twierdzenie Rolle'a pokazuje, że liczby rzeczywiste mają własność Rolle'a. Każde pole algebraicznie domknięte, takie jak liczby zespolone, ma własność Rolle'a. Jednak liczby wymierne nie są – na przykład x 3 − x = x ( x − 1)( x + 1) rozkładają się na czynniki wymierne , ale ich pochodna,
nie. Pytanie, które pola spełniają własność Rolle'a, zostało postawione w ( Kaplansky 1972 ). W przypadku pól skończonych odpowiedź brzmi, że tylko F 2 i F 4 mają własność Rolle'a.
W przypadku wersji złożonej zobacz indeks Voorhoeve .
Zobacz też
- Twierdzenie o wartości średniej
- Twierdzenie o wartości pośredniej
- Interpolacja liniowa
- Twierdzenie Gaussa-Lucasa
Bibliografia
Dalsza lektura
- Leithold, Louis (1972). Rachunek z geometrią analityczną (2nd ed.). Nowy Jork: Harper & Row. s. 201–207. Numer ISBN 0-06-043959-9.
- Taylor, Angus E. (1955). Rachunek zaawansowany . Boston: Ginn i Spółka. s. 30–37.


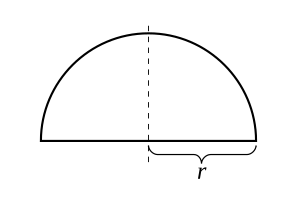
![f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7ef1f348169f09e9db96b68d4b2e73d5f43c156)

![f(x)=|x|,\qquad x\in [-1,1].](https://wikimedia.org/api/rest_v1/media/math/render/svg/106570318bb857ac95a60c075c30a0f40dde84fe)