Ścieżki cząstek w rozwiązaniu Schwarzschilda równań pola Einsteina
W ogólnym wzgl , geodezyjne Schwarzschilda opisu ruchu cząsteczek testowych w polu grawitacyjnym centralnej masy stałej , która, ruchu w Schwarzschilda metryki. Schwarzschilda geodezyjne były decydujące w walidacji Einsteina teorii względności . Na przykład dostarczają dokładnych prognoz anomalnej precesji planet w Układzie Słonecznym i odchylania światła przez grawitację.

Geodezja Schwarzschilda dotyczy tylko ruchu cząstek o masach tak małych, że niewiele wnoszą do pola grawitacyjnego. Są one jednak bardzo dokładne w wielu scenariuszach astrofizycznych, pod warunkiem, że jest wielokrotnie mniejsza niż masa centralna , np. dla planet krążących wokół Słońca. Geodezja Schwarzschilda jest również dobrym przybliżeniem względnego ruchu dwóch ciał o dowolnej masie, pod warunkiem, że masa Schwarzschilda jest równa sumie dwóch indywidualnych mas i . Jest to ważne w przewidywaniu ruchu gwiazd podwójnych w ogólnej teorii względności.





Kontekst historyczny
Metryka Schwarzschilda została nazwana na cześć jej odkrywcy Karla Schwarzschilda , który znalazł rozwiązanie w 1915 roku, zaledwie około miesiąc po opublikowaniu ogólnej teorii względności Einsteina. Było to pierwsze dokładne rozwiązanie równań pola Einsteina inne niż rozwiązanie trywialnej płaskiej przestrzeni .
W 1931 roku Yusuke Hagihara opublikował artykuł pokazujący, że trajektorię cząstki testowej w metryce Schwarzschilda można wyrazić za pomocą funkcji eliptycznych .
Metryka Schwarzschilda
Dokładnym rozwiązaniem równań pola Einsteina jest metryka Schwarzschilda , która odpowiada zewnętrznemu polu grawitacyjnemu nienaładowanego, nie obracającego się, sferycznie symetrycznego ciała masowego . Rozwiązanie Schwarzschilda można zapisać jako


gdzie
-
 to właściwy czas (czas mierzony przez zegar poruszający się z cząsteczką) w sekundach,
to właściwy czas (czas mierzony przez zegar poruszający się z cząsteczką) w sekundach,
-
 to prędkość światła w metrach na sekundę,
to prędkość światła w metrach na sekundę,
-
 jest współrzędną czasową (czas mierzony przez zegar stacjonarny w nieskończoności) w sekundach,
jest współrzędną czasową (czas mierzony przez zegar stacjonarny w nieskończoności) w sekundach,
-
 jest współrzędną promieniową (obwód okręgu o środku gwiazdy podzielony przez ) w metrach,
jest współrzędną promieniową (obwód okręgu o środku gwiazdy podzielony przez ) w metrach,
-
 to colatitude (kąt od północy) w radianach,
to colatitude (kąt od północy) w radianach,
-
 to długość geograficzna w radianach i
to długość geograficzna w radianach i
-
 to promień Schwarzschilda masywnego ciała (w metrach), który jest związany z jego masą przez
to promień Schwarzschilda masywnego ciała (w metrach), który jest związany z jego masą przez


- gdzie jest stała grawitacyjna . Klasyczna teoria grawitacji Newtona jest odtwarzana w granicy, gdy stosunek dochodzi do zera. W tym limicie metryka powraca do wartości określonej przez szczególną teorię względności .


W praktyce stosunek ten jest prawie zawsze bardzo mały. Na przykład promień Schwarzschilda Ziemi wynosi około 9 mm ( 3 ⁄ 8 cali); na powierzchni Ziemi poprawki do grawitacji newtonowskiej są tylko jedną częścią na miliard. Promień Schwarzschilda Słońca jest znacznie większy, około 2953 metrów, ale na jego powierzchni stosunek ten wynosi około 4 części na milion. Biały karzeł gwiazda jest znacznie gęstsza, ale nawet tutaj wskaźnik na jej powierzchni wynosi około 250 części na milion. Stosunek ten staje się duży dopiero w pobliżu bardzo gęstych obiektów, takich jak gwiazdy neutronowe (gdzie stosunek wynosi około 50%) i czarne dziury .


Orbity cząstek testowych

Porównanie orbity cząstki testowej w czasoprzestrzeni Newtona (po lewej) i Schwarzschilda (po prawej); zwróć uwagę na
precesję absydową po prawej stronie.
Możemy uprościć problem, używając symetrii, aby wyeliminować jedną zmienną z rozważań. Ponieważ metryka Schwarzschilda jest symetryczna względem , każda geodezja, która zaczyna się poruszać w tej płaszczyźnie, pozostanie w tej płaszczyźnie przez czas nieokreślony (płaszczyzna jest całkowicie geodezyjna ). Dlatego orientujemy układ współrzędnych tak, aby orbita cząstki leżała w tej płaszczyźnie, i ustalamy współrzędną tak, aby metryka (tej płaszczyzny) była uproszczona do




Można zidentyfikować dwie stałe ruchu (wartości, które nie zmieniają się w odpowiednim czasie ) (por. wyprowadzenie podane poniżej ). Jedna to całkowita energia :



a drugi to specyficzny moment pędu :

gdzie L jest całkowitym momentem pędu dwóch ciał i jest masą zredukowaną . Kiedy zmniejszona masa jest w przybliżeniu równa . Czasami zakłada się, że . W przypadku planety Merkury to uproszczenie wprowadza błąd ponad dwukrotnie większy niż efekt relatywistyczny. Przy omawianiu geodezji można uznać za fikcyjne, a ważne są stałe i . Aby objąć wszystkie możliwe geodezyjne, należy rozważyć przypadki, w których jest nieskończona (podając trajektorie fotonów ) lub urojona (dla geodezji tachionicznej ). Dla przypadku fotonicznego musimy również podać liczbę odpowiadającą stosunkowi dwóch stałych, a mianowicie , która może być zerowa lub niezerowa liczba rzeczywista.









Podstawiając te stałe do definicji metryki Schwarzschilda

daje równanie ruchu dla promienia w funkcji czasu właściwego :


Formalnym rozwiązaniem tego jest:

Zauważ, że pierwiastek kwadratowy będzie urojony dla geodezji tachionicznej.
Używając relacji znajdującej się wyżej między i , możemy również napisać



Ponieważ asymptotycznie całka jest odwrotnie proporcjonalna do , pokazuje to, że w układzie odniesienia, jeśli zbliża się , robi to wykładniczo, nigdy go nie osiągając. Jednak w funkcji , osiąga .







Powyższe rozwiązania są ważne, gdy całka jest skończona, ale rozwiązanie całkowite może obejmować dwie lub nieskończoność części, z których każda jest opisana przez całkę, ale z naprzemiennymi znakami pierwiastka kwadratowego.
Kiedy i , możemy rozwiązać i jednoznacznie:





oraz dla geodezji fotonicznej ( ) z zerowym momentem pędu


(Chociaż właściwy czas jest trywialny w przypadku fotoniki, można zdefiniować parametr afiniczny i wtedy rozwiązaniem równania geodezyjnego jest .)


Innym rozwiązywalnym przypadkiem jest ten, w którym i i są stałe. W objętości, w której to daje na właściwy czas





Jest to bliskie rozwiązaniom z małymi i pozytywnymi. Poza tym rozwiązanie to tachyonic i „właściwy czas” to przestrzeń, jak:




Jest to zbliżone do innych rozwiązań tachionicznych z małym i ujemnym. Stała tachioniczna geodezyjna na zewnątrz nie jest kontynuowana przez stałą geodezyjną wewnątrz , ale raczej kontynuuje się w „równoległym regionie zewnętrznym” (patrz współrzędne Kruskal-Szekeres ). Inne rozwiązania tachioniczne mogą wejść do czarnej dziury i ponownie wyjść do równoległego obszaru zewnętrznego. Stałe t rozwiązanie wewnątrz horyzontu zdarzeń ( ) jest kontynuowane przez stałe t rozwiązanie w białej dziurze .






Gdy moment pędu nie jest zerowy, możemy zastąpić zależność od właściwego czasu zależnością od kąta, korzystając z definicji


co daje równanie orbity

gdzie dla zwięzłości dwie skale długości oraz , zostały zdefiniowane przez



Zauważ, że w przypadku tachionicznym będzie wyimaginowany i rzeczywisty lub nieskończony.


To samo równanie można również wyprowadzić za pomocą podejścia Lagrange'a lub równania Hamiltona-Jacobiego (patrz poniżej ). Rozwiązaniem równania orbity jest

Można to wyrazić za pomocą funkcji eliptycznej Weierstrassa .

Prędkości lokalne i opóźnione
Inaczej niż w mechanice, we współrzędnych Schwarzschilda a nie promieniowe i poprzeczne elementy miejscowego prędkości (w odniesieniu do nieruchomego obserwatora) zamiast dają elementy o celerity które są związane przez







dla promieniowego i

dla poprzecznej składowej ruchu, z . Księgowy współrzędnych daleko od miejsca zdarzenia obserwuje prędkość opóźnioną shapiro , która jest określona zależnością


-
 i .
i .
W formularzu można również umieścić współczynnik dylatacji czasu między księgowym a poruszającą się próbką

gdzie licznik to grawitacja, a mianownik to kinematyczna składowa dylatacji czasu. Dla cząstki opadającej z nieskończoności lewy czynnik jest równy prawemu czynnikowi, ponieważ prędkość opadania odpowiada w tym przypadku prędkości ucieczki .


Dwie stałe: moment pędu i całkowita energia badanej cząstki o masie są wyrażone w




oraz

gdzie

oraz

Dla masywnych cząstek testowych jest to czynnik Lorentza i jest to właściwy czas, podczas gdy dla cząstek bezmasowych, takich jak fotony, jest ustawiony i pełni rolę parametru afinicznego. Jeśli cząstka bezmasowymi jest zastąpiony i z , gdzie jest stałą Plancka , a lokalnie obserwowana częstotliwości.












Dokładne rozwiązanie za pomocą funkcji eliptycznych
Podstawowe równanie orbity jest łatwiejsze do rozwiązania, jeśli jest wyrażone w postaci promienia odwrotnego 

Prawa strona tego równania to wielomian sześcienny , który ma trzy pierwiastki , oznaczane tutaj jako u 1 , u 2 , i u 3

Suma tych trzech pierwiastków równy współczynnik U 2 termin

Wielomian sześcienny o współczynnikach rzeczywistych może mieć albo trzy pierwiastki rzeczywiste, albo jeden pierwiastek rzeczywisty i dwa złożone pierwiastki sprzężone . Jeśli wszystkie trzy pierwiastki są liczbami rzeczywistymi , pierwiastki są oznaczone tak , że u 1 < u 2 < u 3 . Jeśli zamiast tego istnieje tylko jeden prawdziwy pierwiastek, oznaczamy go jako u 3 ; złożone sprzężone korzenie są oznaczone jako u 1 i u 2 . Stosując regułę znaków Kartezjusza , może istnieć co najwyżej jeden pierwiastek ujemny; u 1 jest ujemne wtedy i tylko wtedy, gdy b < a . Jak omówiono poniżej, pierwiastki są przydatne w określaniu typów możliwych orbit.
Biorąc pod uwagę to oznakowanie pierwiastków, rozwiązaniem podstawowego równania orbitalnego jest

gdzie sn reprezentuje funkcję sinus amplitudinus (jedna z funkcji eliptycznych Jacobiego ), a δ jest stałą całkowania odzwierciedlającą pozycję początkową. Moduł eliptyczny k tej funkcji eliptycznej jest określony wzorem

Granica Newtona
Aby uzyskać rozwiązanie newtonowskie dla orbit planet, należy przyjąć granicę, ponieważ promień Schwarzschilda r s zbliża się do zera. W tym przypadku, trzeci korzenia u 3 staje się grubsza , i znacznie większe niż ù 1 OR ù 2 . Dlatego moduł k dąży do zera; w tej granicy sn staje się trygonometryczną funkcją sinus

Zgodnie z rozwiązaniami Newtona dotyczącymi ruchów planet, wzór ten opisuje ogniskową stożkową mimośrodu e

Jeśli u 1 jest dodatnią liczbą rzeczywistą, to orbita jest elipsą, gdzie u 1 i u 2 oznaczają odpowiednio odległości najdalszego i najbliższego podejścia. Jeśli u 1 jest zerem lub ujemną liczbą rzeczywistą, orbita jest odpowiednio parabolą lub hiperbolą . W tych dwóch ostatnich przypadkach u 2 reprezentuje odległość najbliższego zbliżenia; ponieważ orbita zbliża się do nieskończoności ( u = 0), nie ma odległości najdalszego podejścia.
Korzenie i przegląd możliwych orbit
Pierwiastek reprezentuje punkt orbity, w którym znika pochodna, czyli gdzie . W takim punkcie zwrotnym u osiąga maksimum, minimum lub punkt przegięcia w zależności od wartości drugiej pochodnej, która jest wyrażona wzorem

![{\ Displaystyle {\ Frac {d ^ {2} u} {d \ Varphi ^ {2}}} = {\ Frac {R_ {\ RM {s}}} {2}} \ lewo [\ lewo (u- u_{2}\right)\left(u-u_{3}\right)+\left(u-u_{1}\right)\left(u-u_{3}\right)+\left(u- u_{1}\prawo)\lewo(u-u_{2}\prawo)\prawo]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbff935c41511467f9e16003f2e913b861a3216b)
Jeśli wszystkie trzy pierwiastki są różnymi liczbami rzeczywistymi, druga pochodna jest dodatnia, ujemna i dodatnia przy u 1 , u 2 i u 3 . Wynika z tego, że wykres u w funkcji φ może albo oscylować między u 1 i u 2 , albo oddalać się od u 3 w kierunku nieskończoności (co odpowiada r dążącemu do zera). Jeśli u 1 jest ujemne, faktycznie wystąpi tylko część „oscylacji”. Odpowiada to cząstce wychodzącej z nieskończoności, zbliżającej się do masy centralnej, a następnie oddalającej się ponownie w kierunku nieskończoności, podobnie jak trajektoria hiperboliczna w rozwiązaniu klasycznym.
Jeśli cząstka ma odpowiednią ilość energii dla swojego momentu pędu, u 2 i u 3 połączą się. W tym przypadku istnieją trzy rozwiązania. Orbita może kręcić się spiralnie do , zbliżając się do tego promienia jako (asymptotycznie) malejący wykładniczy w φ, τ lub t . Albo można mieć orbitę kołową o tym promieniu. Albo można mieć orbitę, która opada spiralnie od tego promienia do punktu centralnego. Promień, o którym mowa, nazywa się promieniem wewnętrznym i wynosi od do 3 razy r s . Orbita kołowa powstaje również wtedy, gdy u 2 jest równe u 1 i nazywa się to promieniem zewnętrznym. Te różne typy orbit omówiono poniżej.


Jeśli cząstka dociera do masy centralnej z wystarczającą energią i wystarczająco małym momentem pędu, to tylko u 1 będzie rzeczywiste. Odpowiada to cząsteczce wpadającej do czarnej dziury. Orbita skręca się spiralnie ze skończoną zmianą φ.
Precesja orbit
Funkcja sn i jej kwadrat sn 2 mają okresy odpowiednio 4 K i 2 K , gdzie K jest określone równaniem

Dlatego zmiana φ o jedną oscylację u (lub równoważnie jedną oscylację r ) jest równa

W granicy klasycznej u 3 zbliża się i jest znacznie większe niż u 1 lub u 2 . Stąd k 2 jest w przybliżeniu


Z tych samych powodów mianownik Δφ wynosi w przybliżeniu

Ponieważ moduł k jest bliski zeru, okres K można rozszerzyć w potęgach k ; do najniższego rzędu ta ekspansja ustępuje

Podstawienie tych przybliżeń do wzoru na daje wzór na posuw kątowy na oscylację promieniową

W przypadku orbity eliptycznej u 1 i u 2 reprezentują odpowiednio odwrotności najdłuższej i najkrótszej odległości. Można je wyrazić w postaci półosi wielkiej elipsy A i jej mimośrodu orbitalnego e ,

dający

Podstawiając definicję r s otrzymujemy końcowe równanie

Uginanie światła pod wpływem grawitacji
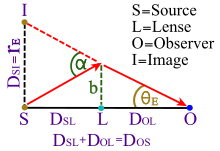
Schemat soczewkowania grawitacyjnego przez kompaktowy korpus
W granicy, gdy masa cząstki m zbliża się do zera (lub, równoważnie, jeśli światło zmierza bezpośrednio w kierunku masy centralnej, gdy skala długości a zbliża się do nieskończoności), równanie orbity staje się

Rozwijając się w potęgach , wiodący wyraz porządku w tym wzorze daje przybliżone odchylenie kątowe δ φ dla bezmasowej cząstki przychodzącej z nieskończoności i wychodzącej z powrotem do nieskończoności:


Tutaj b jest parametrem uderzenia , nieco większym niż odległość najbliższego podejścia , r 3 :

Chociaż ten wzór jest przybliżony, jest dokładny dla większości pomiarów soczewkowania grawitacyjnego , ze względu na mały stosunek . W przypadku światła padającego na powierzchnię Słońca przybliżone odchylenie kątowe wynosi około 1,75 sekundy kątowej , czyli około jednej milionowej części okręgu.

Gdy pakiet fal świetlnych (lub jego kwant, foton) przemieszcza się po odchylonej ścieżce, która jest przewidywana przez zginanie światła, jego funkcja falowa nadal oddziałuje z zakrzywioną geometrią czasoprzestrzeni wokół geodezji i ulega zniekształceniu. Poinformowano, że zniekształcenie jest znaczące w stosunku do poziomu, który można zmierzyć.
Związek z fizyką Newtona
Efektywna promieniowa energia potencjalna
Wyprowadzone powyżej równanie ruchu dla cząstki

można przepisać używając definicji promienia Schwarzschilda r s as
![{\ Displaystyle {\ Frac {1} {2}} m \ lewo ({\ Frac {dr} {d \ tau}} \ prawej) ^ {2} = \ lewo [{\ Frac {E ^ {2}} {2mc^{2}}}-{\frac {1}{2}}mc^{2}\right]+{\frac {GMm}{r}}-{\frac {L^{2}}{ 2\mu r^{2}}}+{\frac {G(M+m)L^{2}}{c^{2}\mu r^{3}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78fa7da802311c62479b99d4078fbaef08a0dbf0)
co jest równoważne cząstce poruszającej się w jednowymiarowym potencjale efektywnym

Pierwsze dwa terminy są dobrze znanymi energiami klasycznymi, pierwszy to przyciągająca newtonowska energia potencjalna grawitacji, a drugi odpowiada odpychającej „odśrodkowej” energii potencjalnej ; jednak trzeci termin to atrakcyjna energia, unikalna dla ogólnej teorii względności . Jak pokazano poniżej i gdzie indziej , ta odwrotna energia sześcienna powoduje stopniową precesję orbit eliptycznych o kąt δφ na obrót

gdzie A to wielka półoś, a e to mimośród.
Trzeci człon jest atrakcyjny i dominuje przy małych wartościach r , dając krytyczny promień wewnętrzny r wewnętrzny, przy którym cząstka jest nieuchronnie przyciągana do środka do r = 0; Ten wewnętrzny promień jest funkcją momentu pędu tych cząstek na jednostkę masy lub równoważnie skala długości określonej powyżej.
Orbity kołowe i ich stabilność
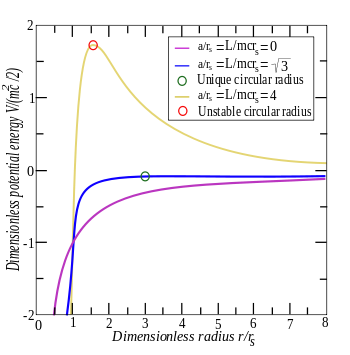
Efektywny potencjał promieniowy dla różnych momentów kątowych. Przy małych promieniach energia gwałtownie spada, powodując nieuchronne przyciąganie cząstki do środka do
r = 0. Jednak gdy znormalizowany moment pędu jest równy pierwiastkowi kwadratowemu z trzech, możliwa jest metastabilna orbita kołowa przy promieniu zaznaczonym zielonym kółkiem . Przy wyższych momentach pędu występuje znaczna bariera odśrodkowa (krzywa pomarańczowa) i niestabilny promień wewnętrzny, zaznaczony na czerwono.

Potencjał efektywny V można przepisać na podstawie długości .

![{\ Displaystyle V (r) = {\ Frac {\ mu c ^ {2}} {2}} \ lewo [- {\ Frac {r_ {\ rm {s}}} {r}} + {\ Frac { a^{2}}{r^{2}}}-{\frac {r_{\rm {s}}a^{2}}{r^{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/532ca22c56a1612492c5e868274d9257f0eba729)
Orbity kołowe są możliwe, gdy efektywna siła wynosi zero
![{\ Displaystyle F = - {\ Frac {dV} {dr}} = - {\ Frac {\ mu c ^ {2}} {2r ^ {4}}} \ lewo [r_ {\ rm {s}} r ^{2}-2a^{2}r+3r_{\rm {s}}a^{2}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/417d63a6c334cbf801d43b95f97d09f8b58ebd7b)
tzn. gdy dwie siły przyciągania — grawitacja newtonowska (pierwszy element) i przyciąganie charakterystyczne dla ogólnej teorii względności (trzeci element) — są dokładnie zrównoważone przez odpychającą siłę odśrodkową (drugi element). Istnieją dwa promienie, przy których może nastąpić to równoważenie, oznaczone tutaj jako r wewnętrzny i r zewnętrzny
![{\ Displaystyle {\ zacząć {wyrównany} r_ {\ tekst {zewnętrzny}} i = {\ Frac {a ^ {2}} {r_ {\ rm {s}}}} \ lewo (1 + {\ sqrt {1 -{\frac {3r_{\rm {s}}^{2}}{a^{2}}}}\right)\\[3pt]r_{\text{wewnętrzna}}&={\frac { a^{2}}{r_{\rm {s}}}}\left(1-{\sqrt {1-{\frac {3r_{\rm {s}}^{2}}{a^{2 }}}}}\right)={\frac {3a^{2}}{r_{\text{zewnętrzny}}}}\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52992e7a17eae29b6c05d60f99a6bd2d9af795bc)
które uzyskuje się za pomocą wzoru kwadratowego . Wewnętrzny promień r wewnętrzny jest niestabilny, ponieważ przyciągająca trzecia siła wzmacnia się znacznie szybciej niż pozostałe dwie siły, gdy r staje się małe; jeśli cząstka ześlizguje się nieco do wewnątrz z r wewnętrznego (gdzie wszystkie trzy siły są w równowadze), trzecia siła dominuje nad pozostałymi dwoma i przyciąga cząstkę nieubłaganie do środka do r = 0. Jednak na zewnętrznym promieniu orbity kołowe są stabilne; trzeci wyraz jest mniej ważny, a system zachowuje się bardziej jak nierelatywistyczny problem Keplera .
Gdy a jest znacznie większe niż r s (przypadek klasyczny), wzory te stają się w przybliżeniu
![{\ Displaystyle {\ zacząć {wyrównany} r_ {\ tekst {zewnętrzny}} i \ około {\ Frac {2a ^ {2}} {r_ {\ rm {s}}}} \ \ [3 pkt] r_ {\ tekst {wewnętrzny}} i około {\frac {3}{2}}r_{\rm {s}}\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df56aeae454867cb6038bbf8a624a9b34d171a92)
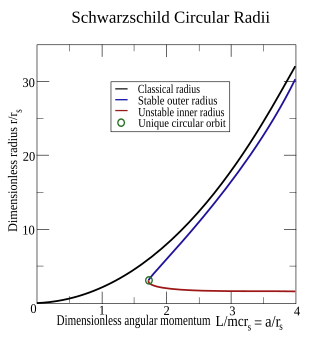
Stabilne i niestabilne promienie są wykreślane w zależności od znormalizowanego momentu pędu odpowiednio w kolorze niebieskim i czerwonym. Krzywe te spotykają się na unikalnej orbicie kołowej (zielone kółko), gdy znormalizowany moment pędu jest równy pierwiastkowi kwadratowemu z trzech. Dla porównania, klasyczny promień przewidywany na podstawie
przyspieszenia dośrodkowego i prawa grawitacji Newtona zaznaczono na czarno.
Podstawienie definicji a i r s na r zewnętrzne daje klasyczny wzór na cząstkę o masie m krążącą wokół ciała o masie M .

gdzie ω φ jest orbitalną prędkością kątową cząstki. Wzór ten uzyskuje się w mechanice nierelatywistycznej przez ustawienie siły odśrodkowej równej Newtonowskiej sile grawitacyjnej:

Gdzie jest zmniejszona masa .

W naszym zapisie klasyczna orbitalna prędkość kątowa równa się

Na drugim końcu, po 2 zbliża 3 r y 2 z góry, dwa promienie zbiegają się w jednej wartości

Powyższe rozwiązania kwadratowe zapewniają, że r zewnętrzne jest zawsze większe niż 3 r s , podczas gdy r wewnętrzne leży między 3 ⁄ 2 r s i 3 r s . Orbity kołowe mniejsze niż 3 ⁄ 2 r s nie są możliwe. Dla cząstek bezmasowych, a idzie do nieskończoności, co oznacza, że fotony mają orbitę kołową przy r inner = 3 ⁄ 2 r s . Sfera o tym promieniu jest czasami nazywana sferą fotonową .
Precesja orbit eliptycznych

W nierelatywistycznym
zagadnieniu Keplera cząstka wiecznie podąża tą samą idealną
elipsą (czerwoną orbitą).
Ogólna teoria względności wprowadza trzecią siłę, która przyciąga cząstkę nieco silniej niż grawitacja newtonowska, zwłaszcza przy małych promieniach. Ta trzecia siła powoduje
preces eliptycznej orbity cząstki (orbita cyjanowa) w kierunku jej rotacji; efekt ten został zmierzony na
Merkurym ,
Wenus i Ziemi. Żółta kropka na orbitach reprezentuje środek przyciągania, taki jak
Słońce .
Szybkość precesji orbitalnej można wyznaczyć przy użyciu tego promieniowego potencjału efektywnego V . Małe odchylenie promieniowe od orbity kołowej o promieniu r zewnętrznym będzie oscylować stabilnie z częstotliwością kątową
![\omega _{r}^{2}={\frac {1}{m}}\left[{\frac {d^{2}V}{dr^{2}}}\right]_{r= r_{\mathrm {zewnętrzny} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894cef5f743b66cd47bfe665608a9fff3e703799)
co równa się

Wyciągnięcie pierwiastka kwadratowego z obu stron i wykonanie rozwinięcia szeregu Taylora daje
![{\ Displaystyle \ omega _ {r} = \ omega _ {\ varphi} \ lewo [1-{\ frac {3r_ {\ rm {s}} ^ {2}} {4a ^ {2}}} + {\ mathcal {O}}\left({\frac {r_{\rm {s}}^{4}}{a^{4}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a71fab0af7c17cf18e5c949ccb3bb3c3bedfc6c4)
Pomnożenie przez okres T jednego obrotu daje precesję orbity na obrót

gdzie użyliśmy ω φ T = 2 п oraz definicję skali długości a . Podstawiając definicję promienia Schwarzschilda r s daje

Można to uprościć za pomocą półosi eliptycznej orbity A i mimośrodu e, związanych wzorem

dać kąt precesji

Matematyczne wyprowadzenia równania orbitalnego
Symbole Christoffela
Nieznikające symbole Christoffela dla metryki Schwarzschilda to:
![{\ Displaystyle {\ zacząć {wyrównany} \ gamma _ {rt} ^ {t} = - \ gamma _ {rr} ^ {r} i = {\ Frac {r_ {\ rm {s}}} {2r (r -r_{\rm {s}})}}\\[3pt]\Gamma _{tt}^{r}&={\frac {r_{\rm {s}}(r-r_{\rm {s }})}{2r^{3}}}\\[3pt]\Gamma _{\phi \phi }^{r}&=(r_{\rm {s}}-r)\sin ^{2} (\theta )\\[3pt]\Gamma _{\theta \theta }^{r}&=r_{\rm {s}}-r\\[3pt]\Gamma _{r\theta }^{\ theta }=\Gamma _{r\phi }^{\phi }&={\frac {1}{r}}\\[3pt]\Gamma _{\phi \phi }^{\theta }&=- \sin(\theta )\cos(\theta )\\[3pt]\Gamma _{\theta \phi }^{\phi }&=\cot(\theta )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ebd981ec7f21f8385ffc13af5084c04f17ae29f)
Równanie geodezyjne
Zgodnie z ogólną teorią względności Einsteina cząstki o znikomej masie przemieszczają się wzdłuż geodezji w czasoprzestrzeni. W płaskiej czasoprzestrzeni, z dala od źródła grawitacji, te geodezyjnie odpowiadają liniom prostym; mogą jednak odbiegać od linii prostych, gdy czasoprzestrzeń jest zakrzywiona. Równanie dla linii geodezyjnych to

gdzie Γ reprezentuje symbol Christoffela, a zmienna parametryzuje drogę cząstki w czasoprzestrzeni , jej tzw. linię świata . Symbol Christoffela zależy tylko od tensora metrycznego , a raczej od tego, jak zmienia się wraz z pozycją. Zmienna jest stałą wielokrotnością czasu właściwego dla orbit czasopodobnych (które podróżują masywne cząstki) i zwykle przyjmuje się, że jest jej równa. Dla lekkich (lub zerowych) orbit (które poruszają się bezmasowe cząstki, takie jak foton ), właściwy czas wynosi zero i, ściśle mówiąc, nie może być używany jako zmienna . Niemniej jednak orbity światłopodobne można wyprowadzić jako ultrarelatywistyczną granicę orbit podobnych do czasu, to znaczy granicę, gdy masa cząstki m spada do zera, przy zachowaniu stałej całkowitej energii .





Dlatego najprostszym sposobem rozwiązania ruchu cząstki jest rozwiązanie równania geodezyjnego, podejście przyjęte przez Einsteina i innych. Metryka Schwarzschilda może być zapisana jako

gdzie dwie funkcje i ich odwrotność są zdefiniowane dla zwięzłości. Z tej metryki można obliczyć symbole Christoffela , a wyniki zastąpić równaniami geodezyjnymi



![{\ Displaystyle {\ zacząć {wyrównany} 0 i = {\ Frac {d ^ {2} \ theta} {dq ^ {2}}} + {\ Frac {2} {r}} {\ Frac {d \ theta} {dq}}{\frac {dr}{dq}}-\sin \theta \cos \theta \left({\frac {d\phi }{dq}}\right)^{2}\\[3pt] 0&={\frac {d^{2}\phi }{dq^{2}}}+{\frac {2}{r}}{\frac {d\phi }{dq}}{\frac {dr }{dq}}+2\cot \theta {\frac {d\phi }{dq}}{\frac {d\theta }{dq}}\\[3pt]0&={\frac {d^{2 }t}{dq^{2}}}+{\frac {1}{w}}{\frac {dw}{dr}}{\frac {dt}{dq}}{\frac {dr}{dq }}\\[3pt]0&={\frac {d^{2}r}{dq^{2}}}+{\frac {1}{2v}}{\frac {dv}{dr}}\ left({\frac {dr}{dq}}\right)^{2}-{\frac {r}{v}}\left({\frac {d\theta }{dq}}\right)^{ 2}-{\frac {r\sin ^{2}\theta }{v}}\left({\frac {d\phi }{dq}}\right)^{2}+{\frac {c^ {2}}{2v}}{\frac {dw}{dr}}\left({\frac {dt}{dq}}\right)^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7c637c4ac82e06d91b30a2a2a9286d4b52ce5f6)
Można sprawdzić, czy jest to poprawne rozwiązanie, podstawiając do pierwszego z tych czterech równań. Zgodnie z symetrią, orbita musi być płaska i możemy dowolnie ustawić układ współrzędnych tak, aby płaszczyzna równika była płaszczyzną orbity. To rozwiązanie upraszcza równania drugie i czwarte.


Aby rozwiązać drugie i trzecie równanie, wystarczy podzielić je odpowiednio przez i .


![{\ Displaystyle {\ zacząć {wyrównany} 0 i = {\ Frac {d} {dq}} \ lewo [\ ln {\ Frac {d \ phi} {dq}} + \ ln r ^ {2} \ prawej] \ \[3pt]0&={\frac {d}{dq}}\left[\ln {\frac {dt}{dq}}+\ln w\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd6b6cb65149f9e94e2aaed1743e7adf905c0aa9)
co daje dwie stałe ruchu.
Podejście Lagrange'a
Ponieważ cząstki testowe podążają za geodezją w ustalonej metryce, orbity tych cząstek można określić za pomocą rachunku wariacji, zwanego również podejściem Lagrange'a. Geodezyjne w czasoprzestrzeni są definiowane jako krzywe, dla których niewielkie lokalne zmiany w ich współrzędnych (przy utrzymywaniu stałych zdarzeń punktów końcowych) nie powodują znaczących zmian w ich całkowitej długości s . Można to wyrazić matematycznie za pomocą rachunku wariacyjnego

gdzie τ jest właściwym czasem , s = cτ jest długością łuku w czasoprzestrzeni, a T jest zdefiniowane jako

analogicznie do energii kinetycznej . Jeśli pochodną po właściwym czasie reprezentuje kropka dla zwięzłości

T można zapisać jako

Czynniki stałe (takie jak c lub pierwiastek kwadratowy z dwóch) nie wpływają na odpowiedź na problem wariacyjny; dlatego przyjęcie wariacji wewnątrz całki daje zasadę Hamiltona

Rozwiązanie problemu wariacyjnego podają równania Lagrange'a

W zastosowaniu do t i φ równania te ujawniają dwie stałe ruchu
![{\ Displaystyle {\ zacząć {wyrównany} {\ Frac {d} {d \ tau}} \ lewo [r ^ {2} {\ Frac {d \ varphi} {d \ tau}} \ po prawej] i = 0, \\{\frac {d}{d\tau }}\left[\left(1-{\frac {r_{\rm {s}}}{r}}\right){\frac {dt}{d \tau }}\right]&=0,\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22ec20bcaa6c2888ba4c6bac76901c7e22fa92be)
co można wyrazić w postaci dwóch stałych skal długości, oraz


Jak pokazano powyżej , podstawienie tych równań do definicji metryki Schwarzschilda daje równanie orbity.
Podejście hamiltonowskie
Rozwiązanie Lagrange'a można przekształcić w równoważną postać Hamiltona. W tym przypadku hamiltonian jest podany przez


Po raz kolejny orbita może być ograniczona przez symetrię. Ponieważ i nie występują w hamiltonianie, ich pędy sprzężone są stałe; mogą być wyrażone jako prędkość światła i dwie stałe skale długości oraz






Pochodne ze względu na właściwy czas są podane przez

Dzielenie pierwszego równania przez drugie daje równanie orbitalne

Promieniowy moment pędu p r może być wyrażony w postaci r przy użyciu stałości hamiltonianu ; daje to podstawowe równanie orbitalne


Podejście Hamiltona-Jacobi
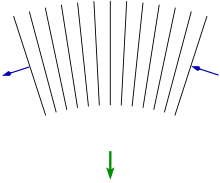
Uginanie fal w polu grawitacyjnym. Ze względu na grawitację czas płynie wolniej na dole niż na górze, powodując, że fronty fal (zaznaczone na czarno) stopniowo zaginają się w dół. Zielona strzałka pokazuje kierunek pozornego „przyciągania grawitacyjnego”.
Równanie orbitalne można wyprowadzić z równania Hamiltona-Jacobiego . Zaletą tego podejścia jest to, że zrównuje ruch cząstki z propagacją fali i prowadzi zgrabnie do wyprowadzenia ugięcia światła przez grawitację w ogólnej teorii względności , za pomocą zasady Fermata . Podstawową ideą jest to, że z powodu grawitacyjnego spowolnienia czasu części frontu fali bliższe masie grawitacyjnej poruszają się wolniej niż te dalej, co powoduje załamanie kierunku propagacji frontu fali.
Korzystając z ogólnej kowariancji, równanie Hamiltona-Jacobiego dla pojedynczej cząstki masy jednostkowej można wyrazić w dowolnych współrzędnych jako

Jest to równoważne z powyższym sformułowaniem hamiltonowskim, w którym pochodne cząstkowe działania zastępują pędy uogólnione. Stosując metrykę Schwarzschilda g μν , równanie to staje się

gdzie ponownie orientujemy sferyczny układ współrzędnych z płaszczyzną orbity. Czas t i kąt azymutalny φ są współrzędnymi cyklicznymi, więc można zapisać
rozwiązanie funkcji głównej Hamiltona S

gdzie i są stałymi uogólnionymi pędami. Równanie Hamilton-Jacobim daje rozwiązanie integralną część promieniowego



Biorąc pochodną funkcji głównej Hamiltona S po zachowanym pędzie p φ daje

co równa się

Przyjęcie nieskończenie małej zmienności φ i r daje podstawowe równanie orbitalne

gdzie zachowane skale długości a i b są określone przez zachowane pędy równaniami

Zasada Hamiltona
Działanie integralną na cząstki oddziałują wyłącznie grawitacja

gdzie jest właściwy czas i jest to dowolna płynna parametryzacja linii świata cząstki. Jeśli zastosujemy do tego rachunek wariacji , otrzymamy ponownie równania dla geodezji. Aby uprościć obliczenia, najpierw bierzemy wariację kwadratu całki. Dla metryki i współrzędnych tego przypadku i zakładając, że cząstka porusza się w płaszczyźnie równikowej , kwadrat ten jest




Biorąc wariację tego daje
![{\ Displaystyle \ delta \ lewo (c {\ Frac {d \ tau} {dq}} \ po prawej) ^ {2} = 2c ^ {2} {\ Frac {d \ tau} {dq}} \ delta {\ frac {d\tau }{dq}}=\delta \left[\left(1-{\frac {r_{\rm {s}}}{r}}\right)c^{2}\left({ \frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{\rm {s}}}{r}}}\left({\ frac {dr}{dq}}\prawo)^{2}-r^{2}\lewo({\frac {d\varphi }{dq}}\prawo)^{2}\prawo]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e86f4747c7f0f42efa826e262657c065f5b51d2)
Ruch w długości geograficznej
Zmieniaj długość geograficzną tylko po to, aby uzyskać


Podziel przez, aby uzyskać zmienność samej całki


Zatem

Integracja przez części daje
![0=-{\frac {r^{{2}}}{c}}{\frac {d\varphi }{d\tau }}\delta \varphi -\int {{\frac {d}{dq} }\left[-{\frac {r^{{2}}}{c}}{\frac {d\varphi }{d\tau }}\right]\delta \varphi dq}\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/102ff196cc6f6db3d1ffe2de3b20869363391073)
Zakłada się, że zmienność długości geograficznej w punktach końcowych wynosi zero, więc pierwszy człon znika. Całka może być niezerowa przez przewrotny wybór, chyba że drugi czynnik wewnątrz jest wszędzie zero. Więc równanie ruchu to

![{\frac {d}{dq}}\lewo[-{\frac {r^{{2}}}{c}}{\frac {d\varphi }{d\tau }}\prawo]=0\ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f671632b4ff69e89141117984215edd0cff34d3f)
Ruch w czasie
Zmieniaj się w zależności od czasu tylko po to, aby uzyskać


Podziel przez, aby uzyskać zmienność samej całki


Zatem

Integracja przez części daje
![{\ Displaystyle 0 = c \ lewo (1-{\ Frac {r_ {\ rm {s}}} {r}} \ prawo) {\ Frac {dt} {d \ tau}} \ delta t-\ int { {\frac {d}{dq}}\left[c\left(1-{\frac {r_{\rm {s}}}{r}}\right){\frac {dt}{d\tau } }\prawo]\delta tdq}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e624938aaeaf72e990427a78b54a1b65b16e10)
Więc równanie ruchu to
![{\ Displaystyle {\ Frac {d} {dq}} \ po lewej [c \ po lewej (1-{\ Frac {r_ {\ rm {s}}} {r}} \ po prawej) {\ Frac {dt} {d \tau }}\prawo]=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a883ea36c8f927bf91a9dd7f61c77a34a29ad825)
Zachowane chwile
Połącz te równania ruchu, aby wyznaczyć stałe całkowania otrzymywania

Te dwa równania dotyczące stałych ruchu (pędu pędu) i (energii) można połączyć w jedno równanie, które jest prawdziwe nawet dla fotonów i innych cząstek bezmasowych, dla których właściwy czas wzdłuż geodezji wynosi zero.



Ruch promieniowy
Zastępowanie

oraz

do równania metrycznego (i używając ) daje


z którego można wywodzić

które jest równaniem ruchu dla . Zależność ON można znaleźć poprzez podzielenie tego przez




dostać

co jest prawdziwe nawet dla cząstek bez masy. Jeśli skale długości są określone przez

oraz

wówczas zależność na uproszczone do



Zobacz też
Uwagi
-
^ To podstawienie u za r jest również powszechne w klasycznych problemach z siłami centralnymi, ponieważ sprawia, że te równania są łatwiejsze do rozwiązania. Więcej informacji można znaleźć w artykule poświęconym klasycznemu problemowi sił centralnych .
-
^ W literaturze matematycznej K jest znane jako całkowita całka eliptyczna pierwszego rodzaju ; więcej informacji można znaleźć w artykule o całkach eliptycznych .
Bibliografia
-
^
Kozai, Yoshihide (1998). „Rozwój Niebiańskiej Mechaniki w Japonii”. Planeta. Nauka o kosmosie . 46 (8): 1031–36. Kod Bibcode : 1998P&SS...46.1031K . doi : 10.1016/s0032-0633(98)00033-6 .
-
^ Landau i Lifszitz, s. 299-301.
-
^ Whittaker 1937.
-
^ Landau i Lifshitz (1975), s. 306-309.
-
^ Gibbons, GW; Vyska, M. (29.02.2012). „Zastosowanie funkcji eliptycznych Weierstrassa do geodezji zerowej Schwarzschilda” . Grawitacja klasyczna i kwantowa . 29 (6). arXiv : 1110,6508 . doi : 10.1088/0264-9381/29/6/065016 .
-
^ Synge, s. 294-295.
-
^ arXiv.org: gr-qc/9907034v1.
-
^
Fizyka komunikacji (13 sierpnia 2021) [ https://twitter.com/CommsPhys/status/1426227181731160069 "@ebi_karimi et al. zgłaszają zniekształcenie zlokalizowanych nośników informacji, wynikające z zakrzywionej geometrii czasoprzestrzeni, ponieważ są one swobodnie transportowane wzdłuż ogólna geodezja"] Twitter.com
-
^ Exirifard, Kasem; Culf, Eric; Karimi, Ebrahim (2021), „W kierunku komunikacji w zakrzywionej geometrii czasoprzestrzeni”, Fizyka komunikacji , 4 (171), arXiv : 2009.04217 , doi : 10.1038/s42005-021-00671-8
-
^ Sean Carroll : Uwagi do wykładu z ogólnej teorii względności , rozdział 7, Eq. 7,33
-
^ Weinberg, s. 122.
-
^ Einstein, s. 95-96.
-
^ Weinberg, s. 185-188; Wald, s. 138-139.
-
^ Synge, s. 290-292; Adler, Bazin i Schiffer, s. 179–182; Whittaker, s. 390-393; Pauli, s. 167.
-
^ Lanczos, s. 331-338.
-
^ Landau i Lifszitz, s. 306-307; Misner, Thorne i Wheeler, s. 636–679.
Bibliografia
- Schwarzschild, K. (1916). Über das Gravitationsfeld eines Massenpunktes nach der Einstein'schen Theorie. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 1 , 189-196.
- Schwarzschild, K. (1916). Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 1 , 424-?.
-
Flamm, L (1916). „Beiträge zur Einstein'schen Gravitationstheorie”. Physikalische Zeitschrift . 17 : 448–?.
-
Adler, R; Bazin M; Schiffera M (1965). Wprowadzenie do ogólnej teorii względności . Nowy Jork: McGraw-Hill Book Company. s. 177 -193. Numer ISBN 978-0-07-000420-7.
-
Einstein, A (1956). Znaczenie względności (wyd. 5). Princeton, New Jersey: Princeton University Press. str. 92 -97. Numer ISBN 978-0-691-02352-6.
-
Hagihara, Y (1931). „Teoria relatywistycznych trajektorii w polu grawitacyjnym Schwarzschilda”. Japoński Dziennik Astronomii i Geofizyki . 8 : 67–176. ISSN 0368-346X .
-
Lanczosa, C (1986). Wariacyjne zasady mechaniki (wyd. 4). Nowy Jork: Dover Publikacje. s. 330–338. Numer ISBN 978-0-486-65067-8.
-
Landau, LD ; Lifszitz, EM (1975). Klasyczna teoria pól . Kurs Fizyki Teoretycznej . Tom. 2 (zrewidowane 4-te wyd. angielskie). Nowy Jork: Pergamon Press. s. 299–309. Numer ISBN 978-0-08-018176-9.
-
Misner, CW ; Thorne, K i Wheeler, JA (1973). Grawitacja . San Francisco: WH Freeman. s. Rozdział 25 (s. 636–687), §33.5 (s. 897–901) oraz §40.5 (s. 1110–1116). Numer ISBN 978-0-7167-0344-0.(Zobacz Grawitacja (książka) .)
-
Pais, A. (1982). Subtelny jest Pan: Nauka i życie Alberta Einsteina . Oxford University Press. s. 253–256 . Numer ISBN 0-19-520438-7.
-
Pauli, W (1958). Teoria względności . Tłumaczone przez G. Fielda. Nowy Jork: Dover Publikacje. str. 40 -41, 166-169. Numer ISBN 978-0-486-64152-2.
-
Rindler, W (1977). Podstawowa teoria względności: specjalna, ogólna i kosmologiczna (poprawione wyd. 2). Nowy Jork: Springer Verlag. s. 143 -149. Numer ISBN 978-0-387-10090-6.
-
Roseveare, NT (1982). Peryhelium Merkurego, od Leverriera do Einsteina . Oxford: Wydawnictwo uniwersyteckie. Numer ISBN 0-19-858174-2.
Zewnętrzne linki
-
Wyciąg z Refleksje na temat względności Kevin Brown.








































































































![{\ Displaystyle {\ Frac {d ^ {2} u} {d \ Varphi ^ {2}}} = {\ Frac {R_ {\ RM {s}}} {2}} \ lewo [\ lewo (u- u_{2}\right)\left(u-u_{3}\right)+\left(u-u_{1}\right)\left(u-u_{3}\right)+\left(u- u_{1}\prawo)\lewo(u-u_{2}\prawo)\prawo]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbff935c41511467f9e16003f2e913b861a3216b)











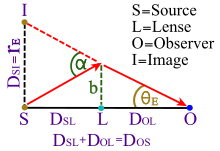





![{\ Displaystyle {\ Frac {1} {2}} m \ lewo ({\ Frac {dr} {d \ tau}} \ prawej) ^ {2} = \ lewo [{\ Frac {E ^ {2}} {2mc^{2}}}-{\frac {1}{2}}mc^{2}\right]+{\frac {GMm}{r}}-{\frac {L^{2}}{ 2\mu r^{2}}}+{\frac {G(M+m)L^{2}}{c^{2}\mu r^{3}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78fa7da802311c62479b99d4078fbaef08a0dbf0)




![{\ Displaystyle V (r) = {\ Frac {\ mu c ^ {2}} {2}} \ lewo [- {\ Frac {r_ {\ rm {s}}} {r}} + {\ Frac { a^{2}}{r^{2}}}-{\frac {r_{\rm {s}}a^{2}}{r^{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/532ca22c56a1612492c5e868274d9257f0eba729)
![{\ Displaystyle F = - {\ Frac {dV} {dr}} = - {\ Frac {\ mu c ^ {2}} {2r ^ {4}}} \ lewo [r_ {\ rm {s}} r ^{2}-2a^{2}r+3r_{\rm {s}}a^{2}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/417d63a6c334cbf801d43b95f97d09f8b58ebd7b)
![{\ Displaystyle {\ zacząć {wyrównany} r_ {\ tekst {zewnętrzny}} i = {\ Frac {a ^ {2}} {r_ {\ rm {s}}}} \ lewo (1 + {\ sqrt {1 -{\frac {3r_{\rm {s}}^{2}}{a^{2}}}}\right)\\[3pt]r_{\text{wewnętrzna}}&={\frac { a^{2}}{r_{\rm {s}}}}\left(1-{\sqrt {1-{\frac {3r_{\rm {s}}^{2}}{a^{2 }}}}}\right)={\frac {3a^{2}}{r_{\text{zewnętrzny}}}}\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52992e7a17eae29b6c05d60f99a6bd2d9af795bc)
![{\ Displaystyle {\ zacząć {wyrównany} r_ {\ tekst {zewnętrzny}} i \ około {\ Frac {2a ^ {2}} {r_ {\ rm {s}}}} \ \ [3 pkt] r_ {\ tekst {wewnętrzny}} i około {\frac {3}{2}}r_{\rm {s}}\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df56aeae454867cb6038bbf8a624a9b34d171a92)




![\omega _{r}^{2}={\frac {1}{m}}\left[{\frac {d^{2}V}{dr^{2}}}\right]_{r= r_{\mathrm {zewnętrzny} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894cef5f743b66cd47bfe665608a9fff3e703799)

![{\ Displaystyle \ omega _ {r} = \ omega _ {\ varphi} \ lewo [1-{\ frac {3r_ {\ rm {s}} ^ {2}} {4a ^ {2}}} + {\ mathcal {O}}\left({\frac {r_{\rm {s}}^{4}}{a^{4}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a71fab0af7c17cf18e5c949ccb3bb3c3bedfc6c4)



![{\ Displaystyle {\ zacząć {wyrównany} \ gamma _ {rt} ^ {t} = - \ gamma _ {rr} ^ {r} i = {\ Frac {r_ {\ rm {s}}} {2r (r -r_{\rm {s}})}}\\[3pt]\Gamma _{tt}^{r}&={\frac {r_{\rm {s}}(r-r_{\rm {s }})}{2r^{3}}}\\[3pt]\Gamma _{\phi \phi }^{r}&=(r_{\rm {s}}-r)\sin ^{2} (\theta )\\[3pt]\Gamma _{\theta \theta }^{r}&=r_{\rm {s}}-r\\[3pt]\Gamma _{r\theta }^{\ theta }=\Gamma _{r\phi }^{\phi }&={\frac {1}{r}}\\[3pt]\Gamma _{\phi \phi }^{\theta }&=- \sin(\theta )\cos(\theta )\\[3pt]\Gamma _{\theta \phi }^{\phi }&=\cot(\theta )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ebd981ec7f21f8385ffc13af5084c04f17ae29f)







![{\ Displaystyle {\ zacząć {wyrównany} 0 i = {\ Frac {d ^ {2} \ theta} {dq ^ {2}}} + {\ Frac {2} {r}} {\ Frac {d \ theta} {dq}}{\frac {dr}{dq}}-\sin \theta \cos \theta \left({\frac {d\phi }{dq}}\right)^{2}\\[3pt] 0&={\frac {d^{2}\phi }{dq^{2}}}+{\frac {2}{r}}{\frac {d\phi }{dq}}{\frac {dr }{dq}}+2\cot \theta {\frac {d\phi }{dq}}{\frac {d\theta }{dq}}\\[3pt]0&={\frac {d^{2 }t}{dq^{2}}}+{\frac {1}{w}}{\frac {dw}{dr}}{\frac {dt}{dq}}{\frac {dr}{dq }}\\[3pt]0&={\frac {d^{2}r}{dq^{2}}}+{\frac {1}{2v}}{\frac {dv}{dr}}\ left({\frac {dr}{dq}}\right)^{2}-{\frac {r}{v}}\left({\frac {d\theta }{dq}}\right)^{ 2}-{\frac {r\sin ^{2}\theta }{v}}\left({\frac {d\phi }{dq}}\right)^{2}+{\frac {c^ {2}}{2v}}{\frac {dw}{dr}}\left({\frac {dt}{dq}}\right)^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7c637c4ac82e06d91b30a2a2a9286d4b52ce5f6)


![{\ Displaystyle {\ zacząć {wyrównany} 0 i = {\ Frac {d} {dq}} \ lewo [\ ln {\ Frac {d \ phi} {dq}} + \ ln r ^ {2} \ prawej] \ \[3pt]0&={\frac {d}{dq}}\left[\ln {\frac {dt}{dq}}+\ln w\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd6b6cb65149f9e94e2aaed1743e7adf905c0aa9)






![{\ Displaystyle {\ zacząć {wyrównany} {\ Frac {d} {d \ tau}} \ lewo [r ^ {2} {\ Frac {d \ varphi} {d \ tau}} \ po prawej] i = 0, \\{\frac {d}{d\tau }}\left[\left(1-{\frac {r_{\rm {s}}}{r}}\right){\frac {dt}{d \tau }}\right]&=0,\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22ec20bcaa6c2888ba4c6bac76901c7e22fa92be)






















![{\ Displaystyle \ delta \ lewo (c {\ Frac {d \ tau} {dq}} \ po prawej) ^ {2} = 2c ^ {2} {\ Frac {d \ tau} {dq}} \ delta {\ frac {d\tau }{dq}}=\delta \left[\left(1-{\frac {r_{\rm {s}}}{r}}\right)c^{2}\left({ \frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{\rm {s}}}{r}}}\left({\ frac {dr}{dq}}\prawo)^{2}-r^{2}\lewo({\frac {d\varphi }{dq}}\prawo)^{2}\prawo]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e86f4747c7f0f42efa826e262657c065f5b51d2)




![0=-{\frac {r^{{2}}}{c}}{\frac {d\varphi }{d\tau }}\delta \varphi -\int {{\frac {d}{dq} }\left[-{\frac {r^{{2}}}{c}}{\frac {d\varphi }{d\tau }}\right]\delta \varphi dq}\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/102ff196cc6f6db3d1ffe2de3b20869363391073)

![{\frac {d}{dq}}\lewo[-{\frac {r^{{2}}}{c}}{\frac {d\varphi }{d\tau }}\prawo]=0\ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f671632b4ff69e89141117984215edd0cff34d3f)



![{\ Displaystyle 0 = c \ lewo (1-{\ Frac {r_ {\ rm {s}}} {r}} \ prawo) {\ Frac {dt} {d \ tau}} \ delta t-\ int { {\frac {d}{dq}}\left[c\left(1-{\frac {r_{\rm {s}}}{r}}\right){\frac {dt}{d\tau } }\prawo]\delta tdq}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e624938aaeaf72e990427a78b54a1b65b16e10)
![{\ Displaystyle {\ Frac {d} {dq}} \ po lewej [c \ po lewej (1-{\ Frac {r_ {\ rm {s}}} {r}} \ po prawej) {\ Frac {dt} {d \tau }}\prawo]=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a883ea36c8f927bf91a9dd7f61c77a34a29ad825)










