Funkcja specjalna określona przez całkę
W całkowego An eliptyczny integralną jest jednym z wielu powiązanych ze sobą funkcje zdefiniowane jako wartości określonych całki. Początkowo powstały one w związku z problemem znalezienia długość łuku danego elipsy i po raz pierwszy badany przez Giulio FAGNANO i Leonhard Euler ( ok. 1750 ). Współczesna matematyka definiuje „całkę eliptyczną” jako dowolną funkcję f, którą można wyrazić w postaci

gdzie R jest funkcją wymierną dwóch jej argumentów, P jest wielomianem stopnia 3 lub 4 bez powtarzających się pierwiastków, a c jest stałą.
Na ogół całki w tej postaci nie mogą być wyrażone w kategoriach funkcji elementarnych . Wyjątkiem od tej ogólnej reguły są sytuacje, w których P ma powtarzające się pierwiastki lub gdy R ( x , y ) nie zawiera nieparzystych potęg y . Jednak przy odpowiednim wzorze redukcyjnym , każdą całkę eliptyczną można sprowadzić do postaci obejmującej całki po funkcjach wymiernych oraz trzy formy kanoniczne Legendre'a (tj. całki eliptyczne pierwszego, drugiego i trzeciego rodzaju).
Oprócz postaci Legendre'a podanej poniżej, całki eliptyczne mogą być również wyrażone w postaci symetrycznej Carlsona . Dodatkowy wgląd w teorię całki eliptycznej można uzyskać, badając odwzorowanie Schwarza-Christoffela . Historycznie funkcje eliptyczne zostały odkryte jako funkcje odwrotne całek eliptycznych.
Notacja argumentów
Niepełne całki eliptyczne są funkcjami dwóch argumentów; całki eliptyczne zupełne są funkcjami jednego argumentu. Argumenty te są wyrażane na wiele różnych, ale równoważnych sposobów (dają tę samą całkę eliptyczną). Większość tekstów trzyma się kanonicznego schematu nazewnictwa, stosując następujące konwencje nazewnictwa.
Za wyrażenie jednego argumentu:
Każda z powyższych trzech wielkości jest całkowicie określona przez którąkolwiek z pozostałych (biorąc pod uwagę, że są one nieujemne). Dzięki temu mogą być używane zamiennie.
Drugi argument może być podobnie wyrażony jako φ , amplituda , lub jako x lub u , gdzie x = sin φ = sn u i sn jest jedną z eliptycznych funkcji jakobianu .
Podanie wartości jednej z tych wielkości determinuje pozostałe. Zauważ, że u zależy również od m . Niektóre dodatkowe relacje z udziałem ciebie obejmują

Ta ostatnia jest czasami nazywana amplitudą delta i zapisywana jako Δ( φ ) = dn u . Czasami w literaturze również odnosi się do parametru komplementarnego , na komplementarny moduł, lub komplementarny kąt modułowej . Zostały one dokładniej zdefiniowane w artykule dotyczącym okresów kwartalnych .
Niepełna całka eliptyczna pierwszego rodzaju
Niekompletny eliptyczną całkę pierwszego rodzaju F określa się jako

To jest postać trygonometryczna całki; zastępując t = sin θ i x = sin φ , otrzymujemy normalną postać Legendre'a:

Odpowiednio pod względem amplitudy i kąta modułowego mamy:

W tym zapisie użycie pionowej kreski jako ogranicznika wskazuje, że argument następujący po nim jest „parametrem” (jak zdefiniowano powyżej), podczas gdy odwrotny ukośnik wskazuje, że jest to kąt modularny. Użycie średnika oznacza, że argument poprzedzający jest sinusem amplitudy:

To potencjalnie mylące użycie różnych ograniczników argumentów jest tradycyjne w całkach eliptycznych, a znaczna część zapisu jest zgodna z zapisem użytym w podręczniku Abramowitza i Steguna oraz użytym w integralnych tablicach Gradsztejna i Ryżika .
Przy x = sn( u , k ) mamy:

zatem jakobian funkcje eliptyczne są odwrotnością całek eliptycznych.
Niepełna całka eliptyczna pierwszego rodzaju ma następujące twierdzenie o dodawaniu:
![{\ Displaystyle F [\ Arctan (x), k] + F [\ Arctan (y), k] = F \ lewo [\ Arctan \ lewo ({\ Frac {x {\ sqrt {k' ^ {2} y) ^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{ 2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee3855e9b2ffc2f73fc5142aaead74e5bcc0238)
Moduł eliptyczny można przekształcić w ten sposób:
![{\ Displaystyle F [\ arcsin (x), k] = {\ Frac {2} {1+ {\ sqrt {1-k ^ {2}}}}} F \ lewo [\ Arcsin \ lewo [{\ Frac {(1+{\sqrt {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ca0a87a094baa6bf1f142f99e81514692d2f872)
Warianty notacyjne
W literaturze stosowane są jeszcze inne konwencje zapisu całek eliptycznych. Notacja z zamiennymi argumentami, F ( k , φ ) , jest często spotykana; i podobnie E ( k , φ ) dla całki drugiego rodzaju. Abramowitz i Stegun podstawiają całkę pierwszego rodzaju F ( φ , k ) za argument φ w ich definicji całek drugiego i trzeciego rodzaju, chyba że po tym argumencie występuje pionowa kreska: tj. E ( F ( φ , k ) | k 2 ) dla E ( φ | k 2 ) . Ponadto ich całki zupełne wykorzystują parametr k 2 jako argument zamiast modułu k , tj. K ( k 2 ) zamiast K ( k ) . Oraz integralny z trzeciego rodzaju zdefiniowanego przez Gradshteyn i Ryzhik , Õ ( cp , n , k ) , umieszcza amplituda φ pierwszy i nie „charakterystyczne” n .
Dlatego podczas korzystania z tych funkcji należy uważać na notację, ponieważ różne renomowane referencje i pakiety oprogramowania używają różnych konwencji w definicjach funkcji eliptycznych. Na przykład, niektóre odnośniki oraz oprogramowanie Wolfram 's Mathematica i Wolfram Alpha definiują całkowitą całkę eliptyczną pierwszego rodzaju pod względem parametru m zamiast modułu eliptycznego k .

Niepełna całka eliptyczna drugiego rodzaju
Niekompletny eliptyczną całkę drugiego rodzaju E w postaci trygonometrycznych jest

Podstawiając t = sin θ i x = sin φ , otrzymujemy normalną postać Legendre'a:

Odpowiednio pod względem amplitudy i kąta modułowego:

Związki z funkcjami eliptycznymi Jacobiego obejmują:

Południk łuk długości od równika do szerokości cp jest napisane w kategoriach E :

gdzie a to wielka półoś , a e to mimośród .
Niepełna całka eliptyczna drugiego rodzaju ma następujące twierdzenie o dodawaniu:
![{\ Displaystyle E [\ Arctan (x), k] + E [\ Arctan (y), k] = E \ lewo [\ Arctan \ lewo ({\ Frac {x {\ sqrt {k '^ {2} y) ^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{ 2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]+{\frac {k^{2}xy}{k'^{2}x^ {2}y^{2}+x^{2}+y^{2}+1}}\left({\frac {x{\sqrt {k'^{2}y^{2}+1} }}{\sqrt {y^{2}+1}}}+{\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2 }+1}}}\prawo)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/befdcddfc97edc9a6d0fe290118b77c2c509a14a)
Moduł eliptyczny można przekształcić w ten sposób:
![{\ Displaystyle E [\ arcsin (x), k] = (1 + {\ sqrt {1-k ^ {2}}}) e \ lewo [\ arcsin \ lewo [{\ Frac {(1 + {\ sqrt) {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt { 1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}\right]-{\sqrt {1-k^{2}}}F[\arcsin( x),k]+{\frac {k^{2}x{\sqrt {1-x^{2}}}}{1+{\sqrt {1-k^{2}x^{2}} }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e914e94f842827749d5a08fad29969c7d2b55705)
Niepełna całka eliptyczna trzeciego rodzaju
Niekompletny eliptyczną całkę trzeciego rodzaju Õ jest

lub

Liczba n nazywana jest cechą i może przyjmować dowolną wartość, niezależnie od innych argumentów. Zauważ jednak, że wartość Π(1;
π/2| m ) jest nieskończony, dla dowolnego m .
Związek z funkcjami eliptycznymi jakobianu jest

Długość łuku południka od równika do szerokości geograficznej φ jest również związana ze szczególnym przypadkiem Π :

Całka eliptyczna zupełna pierwszego rodzaju
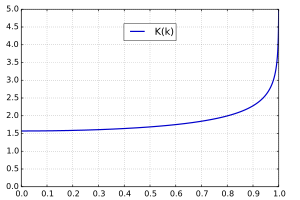
Wykres całkowitej całki eliptycznej pierwszego rodzaju
K ( k )
Całki eliptyczne są uważane za „kompletne”, gdy amplituda φ =π/2a zatem x = 1 . Zakończeniu eliptyczną całkę pierwszego rodzaju K może więc być określony jako

lub bardziej zwięźle w kategoriach całki niezupełnej pierwszego rodzaju jako

Można go wyrazić jako szereg potęgowy

gdzie P n jest wielomianem Legendre'a , który jest równoważny

gdzie n !! oznacza podwójną silnię . W odniesieniu do funkcji hipergeometrycznej Gaussa , całkowitą całkę eliptyczną pierwszego rodzaju można wyrazić jako

Całka eliptyczna pierwszego rodzaju jest czasami nazywana okresem ćwiartkowym . Można ją bardzo sprawnie obliczyć w postaci średniej arytmetyczno-geometrycznej :

Zobacz Carlson (2010 , 19.8) po szczegóły.
Dlatego moduł można przekształcić w ten sposób:
![{\ Displaystyle K (k) = {\ Frac {\ pi} {2 \ operatorname {agm} (1, {\ sqrt {1-k ^ {2}}})}} = {\ Frac {\ pi} 2\operatorname {agm} (1/2+{\sqrt {1-k^{2}}}/2,{\sqrt[{4}]{1-k^{2}}})}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a45040eec194357241ff0f4562b5292bcba1cd83)
![{\ Displaystyle = {\ Frac {\ pi {(1 + {\ sqrt {1-k ^ {2}}}) \ operatorname {agm} [1,2 {\ sqrt [{4}] {1-k ^{2}}}/(1+{\sqrt {1-k^{2}}})]}}={\frac {2}{1+{\sqrt {1-k^{2}}} }}K\left({\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/769c944f72cd0704d3ce2fb91c41dc92326e5277)
To wyrażenie jest ważne dla wszystkich n ∈ ℕ i 0 ≤ k ≤ 1:
![{\ Displaystyle K (k) = n \ lewo [\ suma _ {a = 1} ^ {n} \ nazwa operatora {dn} \ lewo [{\ Frac {2a} {n}} K (k); k \ prawo ]\right]^{-1}K\left[k^{n}\prod _{a=1}^{n}\operatorname {sn} \left[{\frac {2a-1}{n}} K(k);k\right]^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bf6877566831e9d7d844a24f5526cf77c811bc2)
Związek z funkcją Jacobiego theta
Związek z funkcją theta Jacobiego jest podany przez given

gdzie nome Q jest

Wyrażenia asymptotyczne

To przybliżenie ma względną precyzję lepszą niż 3 × 10 -4 dla k <1/2. Zachowanie tylko pierwszych dwóch wyrazów jest poprawne z dokładnością do 0,01 dla k <1/2.
Równanie różniczkowe
Równanie różniczkowe dla całki eliptycznej pierwszego rodzaju to

Drugim rozwiązaniem tego równania jest . To rozwiązanie spełnia relację


Ułamek ciągły
Ułamka rozszerzenia jest:

gdzie nome jest Q = Q ( k ) .
Całka eliptyczna zupełna drugiego rodzaju
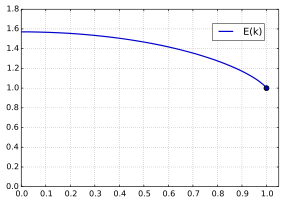
Wykres całkowitej całki eliptycznej drugiego rodzaju

Zakończeniu eliptyczną całkę drugiego rodzaju E jest zdefiniowany jako

lub bardziej zwięźle w kategoriach całki niezupełnej drugiego rodzaju E ( φ , k ) as

Do elipsy półoś a oraz półoś mała b i mimośrodowości e = √ 1 - b 2 / 2 , pełna eliptyczną całkę drugiego rodzaju E ( e ) jest równa jednej czwartej obwodu C z elipsa mierzona w jednostkach wielkiej półosi a . Innymi słowy:

Całą całkę eliptyczną drugiego rodzaju można wyrazić jako szereg potęgowy power

co jest równoważne

W odniesieniu do funkcji hipergeometrycznej Gaussa , całkowitą całkę eliptyczną drugiego rodzaju można wyrazić jako

Moduł można przekształcić w ten sposób:

Obliczenie
Podobnie jak całkę pierwszego rodzaju, całkę eliptyczną drugiego rodzaju można bardzo sprawnie obliczyć przy użyciu średniej arytmetyczno-geometrycznej ( Carlson 2010 , 19.8).
Zdefiniuj sekwencje i , gdzie , oraz relacje cykliczności , przytrzymaj. Ponadto zdefiniuj . Zgodnie z definicją,







-
 .
.
Również . Następnie


W praktyce średnia arytmetyczno-geometryczna byłaby po prostu obliczana do pewnego limitu. Ta formuła jest zbieżna kwadratowo dla wszystkich . Aby jeszcze bardziej przyspieszyć obliczenia, można użyć zależności .


Równanie pochodne i różniczkowe


Drugim rozwiązaniem tego równania jest E ( √1 − k 2 ) − K ( √ 1 − k 2 ) .
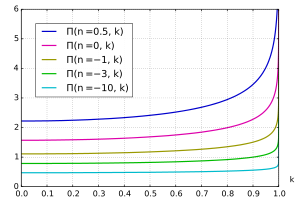
Całka eliptyczna zupełna trzeciego rodzaju
Zakończeniu eliptyczną całkę trzeciego rodzaju Õ można określić jako

Zauważ, że czasami całka eliptyczna trzeciego rodzaju jest definiowana znakiem odwrotnym dla cechy n ,

Podobnie jak zupełne całki eliptyczne pierwszego i drugiego rodzaju, zupełną całkę eliptyczną trzeciego rodzaju można bardzo sprawnie obliczyć przy użyciu średniej arytmetyczno-geometrycznej ( Carlson 2010 , 19,8).
Częściowe pochodne Part
![{\ Displaystyle {\ zacząć {wyrównany} {\ Frac {\ częściowy \ Pi (n, k)} {\ częściowy n}} i = {\ Frac {1} {2 \ lewo (k ^ {2} - n \) right)(n-1)}}\left(E(k)+{\frac {1}{n}}\left(k^{2}-n\right)K(k)+{\frac {1 }{n}}\left(n^{2}-k^{2}\right)\Pi (n,k)\right)\\[10px]{\frac {\częściowy \Pi (n,k) }{\częściowy k}}&={\frac {k}{nk^{2}}}\left({\frac {E(k)}{k^{2}-1}}+\Pi (n ,k)\right)\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff1d0cac8f94db2e3e0b38cef7554432766f458)
Relacje funkcjonalne
Relacja Legendre'a :

Zobacz też
Bibliografia
-
Abramowitz, Milton ; Stegun, Irene Ann , wyd. (1983) [czerwiec 1964]. „Rozdział 17” . Podręcznik funkcji matematycznych z formułami, wykresami i tabelami matematycznymi . Seria matematyki stosowanej. 55 (dziewiąty przedruk z dodatkowymi poprawkami dziesiątego oryginalnego druku z poprawkami (grudzień 1972); wyd. pierwsze). Waszyngton; Nowy Jork: Departament Handlu Stanów Zjednoczonych, Krajowe Biuro Standardów; Publikacje Dovera. str. 587. Numer ISBN 978-0-486-61272-0. LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .
-
Byrd, PF; Friedman, MD (1971). Podręcznik całki eliptycznej dla inżynierów i naukowców (2nd ed.). Nowy Jork: Springer-Verlag. Numer ISBN 0-387-05318-2.
-
Carlson, BC (1995). „Numeryczne obliczanie rzeczywistych lub złożonych całek eliptycznych”. Algorytmy numeryczne . 10 (1): 13–26. arXiv : matematyka/9409227 . Kod bib : 1995NuAlg..10...13C . doi : 10.1007/BF02198293 .
-
Carlson, BC (2010), "Całka eliptyczna" , w Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (red.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
-
Erdélyi, Artur; Magnus, Wilhelm ; Oberhettinger, Fritz; Tricomi, Francesco G. (1953). Wyższe funkcje transcendentalne. Tom II (PDF) . McGraw-Hill Book Company, Inc., Nowy Jork-Toronto-Londyn. MR 0058756 .
-
Gradsztejn, Izrail Solomonovich ; Ryżik, Iosif Moiseevich ; Geronimus, Jurij Weniaminowicz ; Tseytlin, Michaił Yulyevich ; Jeffrey, Alan (2015) [październik 2014]. „8.1.”. W Zwillinger, Daniel; Moll, Victor Hugo (red.). Tabela całek, serii i produktów . Przetłumaczone przez Scripta Technica, Inc. (8 wyd.). Academic Press, Inc. ISBN 978-0-12-384933-5. LCCN 2014010276 .
-
Greenhill, Alfred George (1892). Zastosowania funkcji eliptycznych . Nowy Jork: Macmillan.
-
Hancock, Harris (1910). Wykłady z teorii funkcji eliptycznych . Nowy Jork: J. Wiley i synowie.
-
Król Ludwik V (1924). O bezpośrednim obliczeniu numerycznym funkcji eliptycznych i całek . Wydawnictwo Uniwersytetu Cambridge.
-
Prasa, WH; Teukolski SA; Vetterling, WT; Flannery, BP (2007), „Sekcja 6.12. Całki eliptyczne i jakobian eliptyczne funkcje” , Przepisy numeryczne: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
Linki zewnętrzne








![{\ Displaystyle F [\ Arctan (x), k] + F [\ Arctan (y), k] = F \ lewo [\ Arctan \ lewo ({\ Frac {x {\ sqrt {k' ^ {2} y) ^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{ 2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee3855e9b2ffc2f73fc5142aaead74e5bcc0238)
![{\ Displaystyle F [\ arcsin (x), k] = {\ Frac {2} {1+ {\ sqrt {1-k ^ {2}}}}} F \ lewo [\ Arcsin \ lewo [{\ Frac {(1+{\sqrt {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ca0a87a094baa6bf1f142f99e81514692d2f872)






![{\ Displaystyle E [\ Arctan (x), k] + E [\ Arctan (y), k] = E \ lewo [\ Arctan \ lewo ({\ Frac {x {\ sqrt {k '^ {2} y) ^{2}+1}}}{\sqrt {y^{2}+1}}}\right)+\arctan \left({\frac {y{\sqrt {k'^{2}x^{ 2}+1}}}{\sqrt {x^{2}+1}}}\right),k\right]+{\frac {k^{2}xy}{k'^{2}x^ {2}y^{2}+x^{2}+y^{2}+1}}\left({\frac {x{\sqrt {k'^{2}y^{2}+1} }}{\sqrt {y^{2}+1}}}+{\frac {y{\sqrt {k'^{2}x^{2}+1}}}{\sqrt {x^{2 }+1}}}\prawo)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/befdcddfc97edc9a6d0fe290118b77c2c509a14a)
![{\ Displaystyle E [\ arcsin (x), k] = (1 + {\ sqrt {1-k ^ {2}}}) e \ lewo [\ arcsin \ lewo [{\ Frac {(1 + {\ sqrt) {1-k^{2}}})x}{1+{\sqrt {1-k^{2}x^{2}}}}}\right],{\frac {1-{\sqrt { 1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}\right]-{\sqrt {1-k^{2}}}F[\arcsin( x),k]+{\frac {k^{2}x{\sqrt {1-x^{2}}}}{1+{\sqrt {1-k^{2}x^{2}} }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e914e94f842827749d5a08fad29969c7d2b55705)











![{\ Displaystyle K (k) = {\ Frac {\ pi} {2 \ operatorname {agm} (1, {\ sqrt {1-k ^ {2}}})}} = {\ Frac {\ pi} 2\operatorname {agm} (1/2+{\sqrt {1-k^{2}}}/2,{\sqrt[{4}]{1-k^{2}}})}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a45040eec194357241ff0f4562b5292bcba1cd83)
![{\ Displaystyle = {\ Frac {\ pi {(1 + {\ sqrt {1-k ^ {2}}}) \ operatorname {agm} [1,2 {\ sqrt [{4}] {1-k ^{2}}}/(1+{\sqrt {1-k^{2}}})]}}={\frac {2}{1+{\sqrt {1-k^{2}}} }}K\left({\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/769c944f72cd0704d3ce2fb91c41dc92326e5277)
![{\ Displaystyle K (k) = n \ lewo [\ suma _ {a = 1} ^ {n} \ nazwa operatora {dn} \ lewo [{\ Frac {2a} {n}} K (k); k \ prawo ]\right]^{-1}K\left[k^{n}\prod _{a=1}^{n}\operatorname {sn} \left[{\frac {2a-1}{n}} K(k);k\right]^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bf6877566831e9d7d844a24f5526cf77c811bc2)


































![{\ Displaystyle {\ zacząć {wyrównany} {\ Frac {\ częściowy \ Pi (n, k)} {\ częściowy n}} i = {\ Frac {1} {2 \ lewo (k ^ {2} - n \) right)(n-1)}}\left(E(k)+{\frac {1}{n}}\left(k^{2}-n\right)K(k)+{\frac {1 }{n}}\left(n^{2}-k^{2}\right)\Pi (n,k)\right)\\[10px]{\frac {\częściowy \Pi (n,k) }{\częściowy k}}&={\frac {k}{nk^{2}}}\left({\frac {E(k)}{k^{2}-1}}+\Pi (n ,k)\right)\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff1d0cac8f94db2e3e0b38cef7554432766f458)
