Przepływ skracający krzywą - Curve-shortening flow

Zbieżność krzywej wypukłej z okręgiem pod przepływem skracającym krzywą. Krzywe wewnętrzne (jaśniejszy kolor) to płynne wersje krzywych zewnętrznych. Odstępy czasowe między krzywymi nie są jednolite.

W matematyce przepływ skracający krzywą jest procesem, który modyfikuje gładką krzywą w płaszczyźnie euklidesowej poprzez przesuwanie jej punktów prostopadle do krzywej z prędkością proporcjonalną do krzywizny . Przepływ skracający krzywą jest przykładem przepływu geometrycznego i jest jednowymiarowym przypadkiem przepływu średniej krzywizny . Inne nazwy tego samego procesu to euklidesowy przepływ skracający , geometryczny przepływ ciepła i ewolucja długości łuku .

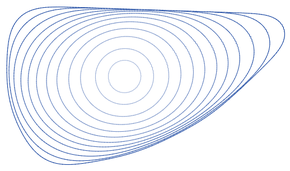
Gdy punkty dowolnej gładkiej prostej zamkniętej krzywej poruszają się w ten sposób, krzywa pozostaje prosta i gładka. Traci obszar w stałym tempie, a jego obwód zmniejsza się tak szybko, jak to możliwe, przy każdej ciągłej ewolucji krzywej. Jeśli krzywa nie jest wypukła, jej całkowita bezwzględna krzywizna zmniejsza się monotonicznie, aż stanie się wypukła. Gdy krzywa jest wypukła, stosunek izoperymetryczny krzywej zmniejsza się, gdy krzywa zbiega się do kształtu kołowego, przed zapadnięciem się do pojedynczego punktu osobliwości. Jeśli dwie rozłączne proste gładkie krzywe zamknięte ewoluują, pozostają one rozłączne, dopóki jedna z nich nie zapadnie się do punktu. Okrąg jest jedyną prostą zamkniętą krzywą, która zachowuje swój kształt pod przepływem skracającym krzywą, ale niektóre krzywe, które przecinają się lub mają nieskończoną długość, zachowują swój kształt, w tym krzywa Ponurego Żniwiarza, nieskończona krzywa, która przesuwa się w górę, i spirale, które się obracają pozostając w tym samym rozmiarze i kształcie.

Przybliżenie przepływu skracającego krzywą można obliczyć numerycznie, przybliżając krzywą jako wielokąt i stosując metodę różnic skończonych do obliczenia ruchu każdego wierzchołka wielokąta. Alternatywne metody obejmują obliczanie splotu wierzchołków wielokąta, a następnie ponowne próbkowanie wierzchołków na powstałej krzywej lub wielokrotne stosowanie filtru mediany do obrazu cyfrowego, którego czarno-białe piksele reprezentują wewnętrzną i zewnętrzną stronę krzywej.

Przepływ skracający krzywą był pierwotnie badany jako model do wyżarzania blach. Później zastosowano go w analizie obrazu, aby uzyskać wieloskalową reprezentację kształtów. Może również modelować układy reakcyjno-dyfuzyjne oraz zachowanie automatów komórkowych . Przepływ skracający krzywą można wykorzystać do znalezienia zamkniętej geodezji na rozmaitościach riemannowskich oraz jako model zachowania przepływów w wyższych wymiarach.

Definicje

Przepływu jest procesem, w którym punkty przestrzeni ciągłą zmianę ich położenia lub właściwości z upływem czasu. Dokładniej, w jednowymiarowym przepływie geometrycznym, takim jak przepływ skracający krzywą, punkty podlegające przepływowi należą do krzywej , a zmienia się kształt krzywej, jej osadzenie w płaszczyźnie euklidesowej określone przez położenie każdego z nich. jego punktów. W przepływie skracającym krzywą każdy punkt krzywej przesuwa się w kierunku wektora normalnego do krzywej, z szybkością proporcjonalną do krzywizny . W przypadku rozwijającej się krzywej reprezentowanej przez funkcję dwuparametrową $C (s, t),$ gdzie $s$ parametryzuje długość łuku wzdłuż krzywej, a $t$ parametryzuje czas w ewolucji krzywej, przepływ skracający krzywą można opisać za pomocą częściowej parabolicznej równanie różniczkowe

{\ Displaystyle {\ Frac {\ częściowy C} {\ częściowy t}} = {\ Frac {\ częściowy ^ {2} C} {\ częściowy s ^ {2}}} = \ kappa n}

postać równania ciepła , gdzie $κ$ jest krzywizną, a $n$ jest jednostkowym wektorem normalnym.

Ponieważ na składniki tego równania, długość łuku, krzywiznę i czas, translacje i obroty płaszczyzny euklidesowej nie mają wpływu, wynika z tego, że przepływ określony przez to równanie jest niezmienny przy translacjach i obrotach (a dokładniej, ekwiwariantnym ). . Jeśli samolot jest skalowany przez stały współczynnik dylatacji, przepływ pozostaje zasadniczo niezmieniony, ale jest spowolniony lub przyspieszony o ten sam współczynnik.

Krzywe niegładkie

Aby przepływ był dobrze zdefiniowany, dana krzywa musi być na tyle gładka, aby miała krzywiznę ciągłą. Jednak po rozpoczęciu przepływu krzywa staje się analityczna i pozostaje taka aż do osiągnięcia osobliwości, w której krzywizna wybucha. W przypadku gładkiej krzywej bez przecięć jedyna możliwa osobliwość ma miejsce, gdy krzywa zapada się do punktu, ale krzywe zanurzone mogą mieć inne rodzaje osobliwości. W takich przypadkach, z pewną ostrożnością, można kontynuować przepływ przez te osobliwości, aż cała krzywa skurczy się do jednego punktu.

W przypadku prostej krzywej zamkniętej, wykorzystującej rozszerzenie przepływu na krzywe niegładkie w oparciu o metodę poziomowania , istnieją tylko dwie możliwości. Krzywe z zerową miarą Lebesgue'a (w tym wszystkie wielokąty i krzywe odcinkowo gładkie) natychmiast ewoluują w gładkie krzywe, po czym ewoluują jak każda gładka krzywa. Jednak krzywe Osgooda z niezerową miarą zamiast tego natychmiast ewoluują w topologiczny pierścień o niezerowej powierzchni i gładkich granicach. W sinusoida zagęszczona jest przykładem, który natychmiast staje się gładka, choć nawet nie jest podłączona lokalnie ; przykłady takie jak ten pokazują, że odwrotna ewolucja przepływu skracającego krzywe może doprowadzić dobrze zachowujące się krzywe do skomplikowanych osobliwości w skończonym czasie.

Powierzchnie nieeuklidesowe

Przepływ skracający krzywą i wiele wyników dotyczących przepływu skracającego krzywą można uogólnić z płaszczyzny euklidesowej na dowolną dwuwymiarową rozmaitość Riemanna . Aby uniknąć dodatkowych typów osobliwości, ważne jest, aby rozmaitość była wypukła w nieskończoności ; oznacza to, że każdy zwarty zbiór ma zwarty kadłub wypukły , zdefiniowany przy użyciu wypukłości geodezyjnej . Przepływ skracający krzywą nie może spowodować odejścia krzywej od jej wypukłego kadłuba, więc warunek ten uniemożliwia częściom krzywej osiągnięcie granicy kolektora.

Krzywe przestrzenne

Przepływ skracający krzywą badano również dla krzywych w trójwymiarowej przestrzeni euklidesowej . Wektor normalny w tym przypadku może być zdefiniowany (jak w płaszczyźnie) jako pochodna wektora stycznego po długości łuku, znormalizowana do wektora jednostkowego; jest to jeden z elementów ramy Frenet-Serret . Nie jest dobrze zdefiniowany w punktach o zerowej krzywiźnie, ale iloczyn krzywizny i wektora normalnego pozostaje dobrze zdefiniowany w tych punktach, co pozwala na określenie przepływu skracającego krzywą. Krzywe w przestrzeni mogą się przecinać lub przecinać się zgodnie z tym przepływem, a przepływ może prowadzić do osobliwości na krzywych; każda osobliwość jest asymptotyczna z płaszczyzną. Wiadomo jednak, że sferyczne krzywe i krzywe, które można rzutować prostopadle na regularną wypukłą krzywą planarną, pozostają proste. Przepływ skracający krzywą dla krzywych przestrzennych został wykorzystany jako sposób zdefiniowania przepływu poza osobliwościami w krzywych płaskich.

Poza krzywymi

Możliwe jest rozszerzenie definicji przepływu na bardziej ogólne dane wejściowe niż krzywe, na przykład poprzez zastosowanie prostowalnych zmiennych lub metody poziomu . Jednak te rozszerzone definicje mogą umożliwiać natychmiastowe znikanie części krzywych lub zagęszczanie ich w zestawy o niezerowej powierzchni.

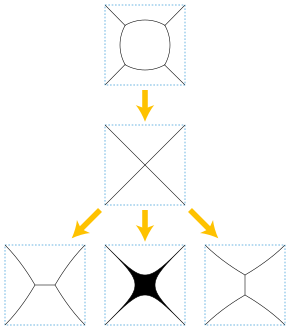
W przypadku sieci krzywych wydłużenie przepływu skracającego krzywą poza osobliwość może skutkować niejednoznacznością lub tuczeniem.

Powszechnie badana odmiana problemu obejmuje sieci wewnętrznych rozłącznych gładkich krzywych, ze skrzyżowaniami, w których spotykają się trzy lub więcej krzywych. Kiedy węzły mają dokładnie trzy krzywe spełniające przy kątach 2 $π$ / 3 (w tych samych warunkach, widzianego w optymalnym Steiner drzewa lub dwuwymiarowym pianki z baniek mydlanych ) przepływ jest dobrze zdefiniowane w krótkim okresie czasu. Jednak może w końcu osiągnąć stan osobliwy z czterema lub więcej krzywymi spotykającymi się na skrzyżowaniu i może istnieć więcej niż jeden sposób na kontynuowanie przepływu przez taką osobliwość.

Zachowanie

Zasada unikania, promień i współczynnik rozciągania

Jeśli dwie rozłączne gładkie proste zamknięte krzywe przechodzą jednocześnie przez przepływ skracający krzywą, pozostają one rozłączne w miarę postępu przepływu. Powodem jest to, że jeśli dwie gładkie krzywe poruszają się w sposób, który tworzy skrzyżowanie, to w momencie pierwszego skrzyżowania krzywe musiałyby być do siebie styczne, bez skrzyżowania. Ale w takiej sytuacji krzywizny dwóch krzywych w punkcie styczności z konieczności rozciągnęłyby je, zamiast zepchnąć w skrzyżowanie. Z tego samego powodu pojedyncza prosta zamknięta krzywa nigdy nie może ewoluować, aby się przeciąć. Zjawisko to znane jest jako zasada unikania.

Zasada unikania oznacza, że każda gładka zamknięta krzywa musi ostatecznie osiągnąć osobliwość, taką jak punkt nieskończonej krzywizny. Bo jeśli dana gładka krzywa $C$ jest otoczona okręgiem, obie pozostaną rozłączne tak długo, jak długo będą istnieć. Ale zamykający się okrąg kurczy się pod wpływem krzywizny, pozostając kołem, aż się zapadnie, i zgodnie z zasadą unikania $C$ musi pozostać w nim. Tak więc, jeśli $C$ nigdy nie osiągnie osobliwości, zostanie uwięzione w jednym punkcie w czasie, gdy okrąg się zapada, co jest niemożliwe dla gładkiej krzywej. Można to określić ilościowo, obserwując, że promień najmniejszego okręgu, który obejmuje $C,$ musi zmniejszać się w tempie co najmniej tak szybkim, jak zmniejszanie się promienia okręgu przechodzącego ten sam przepływ.

Huisken (1998) określa ilościowo zasadę unikania dla pojedynczej krzywej w kategoriach stosunku długości łuku (krótszego z dwóch łuków) do odległości euklidesowej między parami punktów, czasami nazywanej współczynnikiem rozciągnięcia . Pokazuje, że współczynnik rozciągania ściśle maleje w każdym z jego lokalnych maksimów, z wyjątkiem przypadku dwóch końców średnicy koła, w którym współczynnik rozciągania jest stały przy $π$ . Ta właściwość monotoniczności implikuje zasadę unikania, ponieważ gdyby krzywa kiedykolwiek dotknęła się sama, współczynnik rozciągnięcia stałby się nieskończony w dwóch stykających się punktach.

Długość

Gdy krzywa przechodzi przepływ skracający krzywą, jej długość $L$ zmniejsza się w tempie określonym wzorem

{\ Displaystyle {\ Frac {DL} {dt}} = - \ int \ kappa ^ {2} \ ds}

gdzie odstęp jest przejmowany nad krzywą, $κ$ to krzywizna, a $s$ to długość łuku wzdłuż krzywej. Całka jest zawsze nieujemna, a dla każdej gładkiej krzywej zamkniętej istnieją łuki, w których jest ściśle dodatnia, więc długość maleje monotonicznie. Bardziej ogólnie, dla każdej ewolucji krzywych, których normalna prędkość wynosi $f$ , szybkość zmiany długości wynosi

{\ Displaystyle {\ Frac {DL} {dt}} = - \ int f \ kappa \ ds}

co można interpretować jako zanegowany iloczyn wewnętrzny między daną ewolucją a przepływem skracającym krzywą. W ten sposób, przepływ krzywej skracania może być opisana jako gradientem przepływu na długości, w przepływie powietrza (lokalnie) zmniejszenia długości krzywej, tak szybko, jak to możliwe w stosunku do $L 2$ normą przepływu. Ta właściwość jest tą, która nadaje nazwę przepływowi skracania krzywej.

Powierzchnia

W przypadku prostej krzywej zamkniętej obszar zamknięty przez krzywą kurczy się ze stałą szybkością 2 $π$ jednostek powierzchni na jednostkę czasu, niezależnie od krzywej. Dlatego całkowity czas, w którym krzywa skurczy się do punktu, jest proporcjonalna do jej powierzchni, niezależnie od jej początkowego kształtu. Ponieważ pole powierzchni krzywej zmniejsza się w stałym tempie, a (przez nierówność izoperymetryczną ) okrąg ma największą możliwą powierzchnię wśród prostych zamkniętych krzywych o danej długości, wynika z tego, że okręgi są najwolniejszymi krzywymi, które zapadają się do punktu poniżej przepływ skracający krzywą. Wszystkie inne krzywe zapadają się mniej czasu niż okrąg o tej samej długości.

Stałe tempo zmniejszania się powierzchni jest jedynym prawem zachowania spełnianym przez przepływ skracający krzywą. Oznacza to, że nie jest możliwe wyrażenie „punktu zbiegu”, w którym krzywa ostatecznie załamuje się jako całka nad krzywą dowolnej funkcji jej punktów i ich pochodnych, ponieważ takie wyrażenie prowadziłoby do zakazanego drugiego prawa zachowania. Jednak łącząc stałą szybkość utraty powierzchni z zasadą unikania można wykazać, że znikający punkt zawsze leży w okręgu, koncentrycznym z minimalnym otaczającym okręgiem, którego pole jest różnicą pól pomiędzy otaczającym okręgiem a podana krzywa.

Całkowita krzywizna bezwzględna

Całkowity bezwzględna krzywizny gładkiej krzywej całka wartość bezwzględna krzywizny na całej długości łuku krzywej

K=\int |\kappa |\ds.

Może być również wyrażona jako suma kątów między wektorami normalnymi w kolejnych parach punktów przegięcia . Jest to 2 $π$ dla krzywych wypukłych i większe dla krzywych niewypukłych, służąc jako miara niewypukłości krzywej.

Nowe punkty przegięcia nie mogą być tworzone przez przepływ skracający krzywą. Każdy z kątów w reprezentacji całkowitej bezwzględnej krzywizny jako sumy zmniejsza się monotonicznie, z wyjątkiem chwil, gdy dwa kolejne punkty przegięcia osiągają ten sam kąt lub położenie i oba są eliminowane. Dlatego całkowita krzywizna bezwzględna nigdy nie może się zwiększyć w miarę ewolucji krzywej. Dla krzywych wypukłych jest stała i wynosi 2 $π,$ a dla krzywych niewypukłych maleje monotonicznie.

Twierdzenie Gage'a-Hamiltona-Graysona

Jeśli gładka prosta zamknięta krzywa podlega przepływowi skracającemu krzywą, pozostaje gładko osadzona bez samoprzecięć. W końcu stanie się wypukły , a gdy to zrobi, pozostanie wypukły. Po tym czasie wszystkie punkty krzywej przesuną się do wewnątrz, a kształt krzywej zbiegnie się w okrąg, gdy cała krzywa skurczy się do jednego punktu. To zachowanie jest czasami podsumowane stwierdzeniem, że każda prosta zamknięta krzywa kurczy się do „okrągłego punktu”.

Ten wynik jest zasługą Michaela Gage'a , Richarda S. Hamiltona i Matthew Graysona. Gage ( 1983 , 1984 ) udowodnił zbieżność do okręgu dla krzywych wypukłych, które kurczą się do punktu. Dokładniej, Gage wykazał, że stosunek izoperymetryczny (stosunek kwadratowej długości krzywej do powierzchni, liczba, która wynosi 4 $π$ dla okręgu i większa dla każdej innej krzywej wypukłej) zmniejsza się monotonicznie i szybko. Gage i Hamilton (1986) dowiedli, że wszystkie gładkie krzywe wypukłe ostatecznie kurczą się do punktu bez tworzenia innych osobliwości, a Grayson (1987) dowiódł, że każda krzywa niewypukła ostatecznie stanie się wypukła. Andrews i Bryan (2011) dostarczają prostszego dowodu wyniku Graysona, opartego na monotoniczności współczynnika rozciągania.

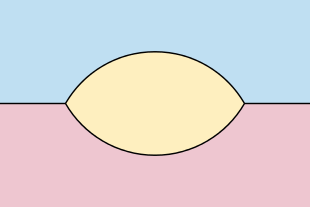
Ograniczający kształt dla wszystkich sieci dwóch promieni współliniowych i dwóch krzywych łączących punkty końcowe dwóch promieni. Soczewka centralna ma kształt vesica piscis .

Podobne wyniki można rozszerzyć od krzywych zamkniętych do krzywych nieograniczonych, spełniających lokalny warunek Lipschitza . W przypadku takich krzywych, jeśli obie strony krzywej mają nieskończoną powierzchnię, to rozwinięta krzywa pozostaje przez cały czas gładka i wolna od osobliwości. Jeśli jednak jedna strona krzywej nieograniczonej ma skończone pole, a krzywa ma skończoną całkowitą krzywiznę bezwzględną, to jej ewolucja osiąga osobliwość w czasie proporcjonalną do pola powierzchni po stronie krzywej o skończonym polu, z nieograniczoną krzywizną w pobliżu osobliwości . W przypadku krzywych, które są wykresami wystarczająco dobrze zachowujących się funkcji, asymptotycznych względem promienia w każdym kierunku, rozwiązanie zbiega się pod względem kształtu do unikalnego kształtu, który jest asymptotyczny względem tych samych promieni. W przypadku sieci utworzonych przez dwa rozłączne promienie na tej samej linii, wraz z dwiema gładkimi krzywymi łączącymi punkty końcowe dwóch promieni, obowiązuje analogia twierdzenia Gage'a-Hamiltona-Graysona, w której obszar między dwiema krzywymi staje się wypukły, a następnie zbiega się do kształtu vesica piscis .

Osobliwości krzywych samoprzecinających się

Krzywe z samoprzecinaniem się mogą osiągnąć punkty osobliwe przed skurczeniem się do punktu. Na przykład, jeśli lemniskata (dowolna gładka, zanurzona krzywa z pojedynczym przecięciem, przypominająca cyfrę 8 lub symbol nieskończoności ) ma nierówne obszary w swoich dwóch płatach, to w końcu mniejszy płat zapadnie się do punktu. Jednakże, jeśli dwa płaty mają równe obszary, to pozostaną one równe przez cały czas ewolucji krzywej, a stosunek izoperymetryczny będzie się różnić, gdy krzywa zapadnie się do osobliwości.

Kiedy lokalnie wypukła krzywa samoprzecinająca się zbliża się do osobliwości, gdy jedna z jej pętli się kurczy, albo kurczy się w podobny sposób, albo asymptotycznie zbliża się do krzywej Ponurego Żniwiarza (opisanej poniżej), gdy się kurczy. Kiedy pętla zapada się w osobliwość, całkowita utrata bezwzględnej krzywizny wynosi co najmniej 2 $π$ lub dokładnie $π$ .

O rozmaitościach riemannowskich

Na rozmaitości riemannowskiej każda gładka prosta krzywa zamknięta pozostanie gładka i prosta w miarę rozwoju, tak jak w przypadku euklidesowym. Albo zapadnie się do pewnego punktu w skończonym czasie, albo pozostanie gładka i prosta na zawsze. W tym drugim przypadku krzywa koniecznie zbiega się do zamkniętej geodezji powierzchni.

Krzywe zanurzone na rozmaitościach riemannowskich, ze skończoną liczbą samoskrzyżowań, stają się samostyczne tylko w dyskretnym zbiorze czasów, w każdym z których gubią przecięcie. W konsekwencji liczba samoprzekraczających się punktów nie wzrasta.

Piłka tenisowa

Skrócenie krzywej na kuli może być użyte jako część dowodu twierdzenia o piłce tenisowej . Twierdzenie to mówi, że każda gładka prosta zamknięta krzywa na kuli, która dzieli powierzchnię kuli na dwa równe obszary (jak szew piłki tenisowej ) musi mieć co najmniej cztery punkty przegięcia . Dowodem na to jest obserwacja, że skrócenie krzywej zachowuje gładkość i właściwości dwusekcji krzywej i nie zwiększa liczby jej punktów przegięcia. Pozwala to zatem sprowadzić problem do problemu dla krzywych w pobliżu granicznego kształtu skrócenia krzywej, wielkiego koła .

Wzór na monotoniczność Huiskena

Zgodnie z formułą monotoniczności Huiskena splot krzywej ewoluującej z odwróconym w czasie jądrem ciepła nie wzrasta. Wynik ten można wykorzystać do analizy osobliwości ewolucji.

Specyficzne krzywe

Krzywe z samopodobną ewolucją

Krzywa Ponurego Żniwiarza i jej przetłumaczone kopie wytworzone przez przepływ skracający krzywą

Ponieważ każda inna prosta zamknięta krzywa zbiega się w okrąg, okrąg jest jedyną prostą zamkniętą krzywą, która zachowuje swój kształt pod przepływem skracającym krzywą. Istnieje jednak wiele innych przykładów krzywych, które są albo nieproste (zawierają samoskrzyżowania), albo niezamknięte (rozciągają się w nieskończoność) i zachowują swój kształt. W szczególności,

Każda linia pozostaje niezmieniona dzięki przepływowi skracającemu krzywą. Linie są jedynymi krzywymi, na które przepływ skracający krzywe nie ma wpływu, chociaż istnieją bardziej złożone, stabilne sieci krzywych, takie jak sześciokątne kafelki płaszczyzny.
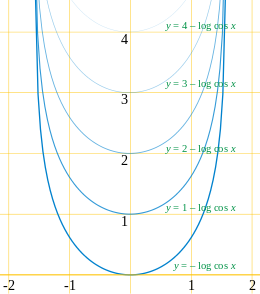
Groźny krzywa żniwiarka $Y = - log cos x$ przemieszcza się w górę bez zmiany jego kształtu. W ten sam sposób każda krzywa podobna do ponurego żniwiarza jest przesuwana przez przepływ skracający krzywą, przesunięty w kierunku osi symetrii krzywej bez zmiany jej kształtu lub orientacji. Ponury żniwiarz jest jedyną krzywą z tą właściwością. W literaturze fizycznej jest również nazywany modelem spinki do włosów .
Rodzina samoprzecinających się zamkniętych krzywych, wyprowadzonych z rzutów węzłów torusowych , kurczy się jednorodnie, ale pozostaje samopodobna w przepływie skracającym krzywą. Zostały one nazwane krzywymi Abrescha–Langera , po pracach Abrescha i Langera (1986) , chociaż zostały wspomniane wcześniej przez Mullinsa (1956) i niezależnie odkryte przez Epsteina i Weinsteina (1987) . Krzywe te są lokalnie wypukłe i dlatego można je opisać ich funkcjami pomocniczymi . Odpowiednio skalowane wersje tych funkcji pomocniczych są zgodne z równaniem różniczkowym
${\ Displaystyle h ''+ h = {\ Frac {1} {h}}}$

który ma dodatnie rozwiązania okresowe (odpowiadające krzywym z samopodobną ewolucją) dla dowolnego okresu, który jest ściśle pomiędzy

π

i .

\pi {\sqrt {2}}

Inne krzywe, w tym niektóre nieskończone spirale , pozostają samopodobne do bardziej skomplikowanych ruchów, w tym obrotu lub kombinacji obrotu, kurczenia się lub rozszerzania oraz translacji.
Dla sieci o gładkich krzywych, spotykających się trójkami na skrzyżowaniach o kątach 2 $π$ /3, samopodobne rozwiązania kurczenia obejmują podwójną bańkę otaczającą dwa równe obszary, kształt soczewki ( vesica piscis ) ograniczony dwoma przystającymi łukami okręgów wraz z dwa promienie współliniowe, których wierzchołki znajdują się w rogach soczewki, oraz sieć w kształcie ryby, ograniczona segmentem linii, dwoma promieniami i krzywą wypukłą. Wszelkie inne samopodobne sieci kurczenia się zawierają większą liczbę krzywych. Inna rodzina sieci rośnie homotetycznie i pozostaje samopodobna; są to drzewiaste sieci krzywych, spotykające się pod kątami 2 $π$ /3 na potrójnych połączeniach, asymptotyczne do wachlarza dwóch lub więcej promieni, które spotykają się we wspólnym punkcie końcowym. Dwupromieniowy przypadek tych kształtów jest nieograniczoną gładką krzywą; dla trzech lub więcej promieni ewolucja tych kształtów może być określona przy użyciu uogólnionych wariantów przepływu skracającego krzywą, takich jak ten dla varifoldów. Dany wachlarz czterech lub więcej promieni może być asymptotyczny do więcej niż jednego innego rozwiązania tego typu, więc rozwiązania te nie dostarczają jednoznacznej definicji przepływu skracającego krzywe zaczynając od wachlarza promieni.

Starożytne rozwiązania

Starożytny rozwiązanie dla problemu przepływowego jest krzywą, której ewolucja można ekstrapolować do tyłu przez cały czas, bez osobliwości. Wszystkie samopodobne rozwiązania, które kurczą się lub pozostają w tym samym rozmiarze, zamiast rosnąć, są w tym sensie rozwiązaniami starożytnymi; można je ekstrapolować wstecz, odwracając transformację samopodobieństwa , której podlegałyby przy przepływie skracającym krzywą do przodu. Tak więc, na przykład, koło, ponury żniwiarz i krzywe Abrescha-Langera są starożytnymi rozwiązaniami.

Są też przykłady, które nie są do siebie podobne. Wyraźnym przykładem jest rozwiązanie owalne Angenent po pracy Angenent (1992) . Tę rodzinę krzywych można sparametryzować, określając krzywiznę w funkcji kąta stycznej za pomocą wzoru

{\ Displaystyle k (\ theta , t) = {\ sqrt {\ cos 2 \ theta - \ operatorname {coth} 2 t}}}

i mają jako ograniczający kształt w odwrotnej ewolucji parę krzywych ponurych żniwiarzy zbliżających się do siebie z przeciwnych kierunków. W kartezjańskim układzie współrzędnych można je podać za pomocą niejawnego równania krzywej

{\ Displaystyle \ cosh ye ^ {-t} \ cos x = 0.}

W literaturze fizyki te same kształty są znane jako model spinacza .

Rozwiązania angenentnego owalu i kurczącego się koła są jedynymi starożytnymi rozwiązaniami, których warstwy czasowe ograniczają ograniczone zbiory wypukłe. Ponury Żniwiarz, stacjonarna półprzestrzeń i stacjonarne rozwiązania wstęgowe to jedyne przykłady, których warstwy czasowe ograniczają nieograniczone zbiory wypukłe. Istnieje wiele dalszych (nieosadzanych) przykładów lokalnie wypukłych, jak również wiele dalszych (niewypukłych) przykładów osadzonych.

Przybliżenia liczbowe

Aby skutecznie obliczyć przepływ skracający krzywą, zarówno krzywa ciągła, jak i ciągła ewolucja krzywej muszą zostać zastąpione przybliżeniem dyskretnym.

Śledzenie z przodu

Metody śledzenia frontu są od dawna stosowane w dynamice płynów do modelowania i śledzenia ruchu granic między różnymi materiałami, stromych gradientów właściwości materiałów, takich jak fronty pogodowe , lub fal uderzeniowych w pojedynczym materiale. Metody te polegają na wyprowadzeniu równań ruchu granicy i wykorzystaniu ich do bezpośredniej symulacji ruchu granicy, zamiast symulowania płynu pod spodem i traktowania granicy jako wyłaniającej się właściwości płynu. Te same metody można również zastosować do symulacji przepływu skracającego krzywą, nawet jeśli krzywa przechodząca przepływ nie jest granicą ani wstrząsem.

W metodach śledzenia frontu skracania krzywej, krzywa podlegająca ewolucji jest dyskretyzowana jako wielokąt. Metoda różnic skończonych służy do wyprowadzania wzorów na przybliżony wektor normalny i krzywiznę w każdym wierzchołku wielokąta, a wartości te są używane do określenia sposobu przesuwania każdego wierzchołka w każdym kroku czasowym. Chociaż przepływ skracający krzywą jest zdefiniowany przez ruch krzywej prostopadle do siebie, niektóre parametryzacje przepływu skracającego krzywą mogą pozwolić wierzchołkom, które aproksymują krzywą, poruszać się nie prostopadle. W efekcie umożliwia to poruszanie się wierzchołków wzdłuż krzywej, gdy krzywa ewoluuje. Wybór ostrożnej ponownej parametryzacji może pomóc w bardziej równomiernym rozmieszczeniu wierzchołków wzdłuż krzywej w sytuacjach, w których ruch prostopadły spowodowałby ich skupienie. Merriman, Bence i Osher (1992) piszą, że metody te są szybkie i dokładne, ale znacznie bardziej skomplikowane jest rozszerzenie ich do wersji przepływu skracania krzywych, które mają zastosowanie do bardziej skomplikowanych danych wejściowych niż prostych krzywych zamkniętych, gdzie konieczne jest radzić sobie z osobliwościami i zmianami topologii.

W przypadku większości takich metod Cao (2003) ostrzega, że „warunki stabilności nie mogą być łatwo określone, a krok czasowy musi być wybierany ad hoc”. Inna metoda różnicowania skończonego autorstwa Crandall i Lions (1996) modyfikuje wzór na krzywiznę w każdym wierzchołku, dodając do niego mały składnik oparty na operatorze Laplace'a . Modyfikacja ta nazywana jest regularyzacją eliptyczną i może być wykorzystana do udowodnienia istnienia uogólnionych przepływów, jak również w ich symulacji numerycznej. Korzystając z niej, można udowodnić, że metoda Crandalla i Lions jest zbieżna i jest jedyną metodą numeryczną wymienioną przez Cao, która jest wyposażona w ograniczenia dotyczące jej szybkości zbieżności. Dla empirycznego porównania przodu Eulera , zacofanym Eulera i uściślenia Crank-Nicolson metody różnic skończonych, zobacz Balažovjech & Mikuła (2009) .

Ponownie próbkowany splot

Mokhtarian i Mackworth (1992) proponują metodę numeryczną do obliczania przybliżenia do przepływu skracającego krzywą, która utrzymuje dyskretne przybliżenie do krzywej i zmienia się między dwoma krokami:

Przeprowadź ponowne próbkowanie bieżącej krzywej, umieszczając nowe punkty próbkowania w równych odstępach, mierzonych przez znormalizowaną długość łuku.
Połącz lokalizacje punktów z funkcją Gaussa z małym odchyleniem standardowym, w efekcie zastępując położenie każdego punktu średnią ważoną lokalizacji pobliskich punktów wzdłuż krzywej, z wagami Gaussa. Odchylenie standardowe Gaussa powinno być wystarczająco małe, aby po tym etapie punkty próbkowania nadal miały prawie jednorodne odstępy.

Jak pokazują, metoda ta zbliża się do rozkładu skrócenia krzywej w limicie wraz ze wzrostem liczby punktów próbkowania i zmniejszaniem się znormalizowanej długości łuku promienia splotu.

Mediana filtrowania

Merriman, Bence i Osher (1992) opisują schemat operujący na dwuwymiarowej siatce kwadratowej – w efekcie na tablicy pikseli . Wyewoluowana krzywa jest reprezentowana przez przypisanie wartości 0 (czarny) pikselom na zewnątrz krzywej i 1 (biały) pikselom wewnątrz krzywej, co daje funkcję wskaźnika dla wnętrza krzywej. Ta reprezentacja jest aktualizowana przez naprzemienne dwa kroki:

Połącz pikselowany obraz z jądrem ciepła, aby symulować jego ewolucję zgodnie z równaniem ciepła w krótkim odstępie czasu. Rezultatem jest rozmycie gaussowskie obrazu lub równoważnie transformata Weierstrassa funkcji wskaźnika, z promieniem proporcjonalnym do pierwiastka kwadratowego kroku czasowego.
Ustaw każdy piksel o wartości liczbowej mniej niż 1/2 do 0, a każdy piksel z numeryczną wartość większą niż 1/2 do 1, wartości odcięcia tył obrazu do jego oryginalnych wartości w nowych miejscach.

Aby ten schemat był dokładny, krok czasowy musi być wystarczająco duży, aby spowodować przesunięcie krzywej o co najmniej jeden piksel nawet w punktach o małej krzywiźnie, ale na tyle mały, aby promień rozmycia był mniejszy niż minimalny promień krzywizny. Dlatego rozmiar piksela musi wynosić $O (min κ /max κ 2)$ , wystarczająco mały, aby umożliwić wybór odpowiedniego pośredniego kroku czasu.

Metodę można uogólnić na ewolucję sieci krzywych, spotykających się na skrzyżowaniach i dzielących płaszczyznę na więcej niż trzy obszary, stosując tę samą metodę jednocześnie do każdego obszaru. Zamiast rozmycia i progowania, tę metodę można alternatywnie opisać jako zastosowanie filtru mediany z wagami Gaussa do każdego piksela. Możliwe jest użycie jąder innych niż jądro cieplne lub adaptacyjne udoskonalenie siatki tak, aby miała wysoką rozdzielczość w pobliżu krzywej, ale nie marnowała czasu i pamięci na piksele daleko od krzywej, które nie wpływają na wynik. Zamiast używać tylko dwóch wartości w obrazie podzielonym na piksele, wersja tej metody, która używa obrazu, którego wartości pikseli reprezentują podpisaną odległość od krzywej, może osiągnąć dokładność subpikseli i wymagać niższej rozdzielczości.

Aplikacje

Wyżarzanie blach

Wczesne odniesienie do przepływu skracającego krzywą przez Williama W. Mullinsa ( 1956 ) uzasadnia to jako model fizycznego procesu wyżarzania , w którym obróbka cieplna powoduje przesunięcie granic między ziarnami skrystalizowanego metalu. W przeciwieństwie do filmów mydlanych , które w wyniku różnic ciśnienia powietrza stają się powierzchniami o stałej średniej krzywiźnie , granice ziaren w wyżarzaniu podlegają tylko lokalnym efektom, które powodują ich ruch zgodnie ze średnią krzywizną. Jednowymiarowy przypadek tego przepływu, przepływ skracający krzywą, odpowiada wyżarzaniu blach, które są wystarczająco cienkie, aby ziarna stały się efektywnie dwuwymiarowe, a ich granice stały się jednowymiarowe.

Analiza kształtu

W przetwarzaniu obrazu i wizji komputerowej , Mokhtarian & Mackworth (1992) sugerują zastosowanie przepływu krzywej skrócenie do zarysu kształtu pochodzącej z obrazu cyfrowego, aby usunąć szum z kształtu i zapewniają przestrzeń skalę , która zapewnia uproszczony opis kształtu na różnych poziomach rozdzielczości. Metoda Mokhtariana i Mackwortha polega na obliczeniu przepływu skracającego krzywą, śledzeniu punktów przegięcia krzywej w miarę ich postępu oraz rysowaniu wykresu przedstawiającego pozycje punktów przegięcia wokół krzywej w funkcji czasu. Punkty przegięcia będą zazwyczaj usuwane z krzywej parami, gdy krzywa staje się wypukła (zgodnie z twierdzeniem Gage'a-Hamiltona-Graysona), a czas życia pary punktów odpowiada istotności cechy kształtu. Ze względu na metodę splotu resampled, którą opisują do obliczania numerycznego przybliżenia przepływu skracającego krzywą, nazywają swoją metodę przestrzenią skali resampled krzywizny . Zauważają, że ta przestrzeń skali jest niezmienna w euklidesowych przekształceniach danego kształtu i twierdzą, że jednoznacznie determinuje kształt i jest odporna na małe zmiany kształtu. Porównują ją eksperymentalnie z kilkoma powiązanymi alternatywnymi definicjami przestrzeni skali dla kształtów i stwierdzają, że ponownie próbkowana przestrzeń skali krzywizny jest mniej intensywna obliczeniowo, bardziej odporna na niejednorodny szum i mniej silnie pod wpływem różnic kształtu w małej skali.

Reakcja-dyfuzja

W układach reakcji i dyfuzji modelowanych równaniem Allena-Cahna , ograniczające zachowanie dla szybkiej reakcji, powolnej dyfuzji i dwóch lub więcej lokalnych minimów energii o tym samym poziomie energii, jak każdy inny, ma na celu osiedlenie się systemu w regionach o różnych lokalnych minima, przy czym fronty wyznaczające granice między tymi regionami ewoluują zgodnie z przepływem skracającym krzywą.

Automaty komórkowe

Automat komórkowy Anneal, 1600 kroków po losowym uruchomieniu

W automacie komórkowym każda komórka w nieskończonej siatce komórek może mieć jeden ze skończonego zbioru stanów, a wszystkie komórki aktualizują swoje stany jednocześnie tylko na podstawie konfiguracji małego zbioru sąsiednich komórek. Życie jak komórkowym automatu reguły jest jeden, w którym siatka jest nieskończony kwadratowy kraty, istnieją dokładnie dwa stany komórkowe, zbiór sąsiadów każdej komórki są osiem sąsiedzi okolicy Moore , a reguła zmiana zależy tylko od liczby sąsiadów z każdym z dwóch stanów, a nie na jakiejkolwiek bardziej skomplikowanej funkcji tych stanów. W jednej konkretnej, podobnej do życia regule, wprowadzonej przez Gerarda Vichniaca i zwanej regułą skręconej większości lub regułą wyżarzania, reguła aktualizacji ustala nową wartość dla każdej komórki jako większości spośród dziewięciu podanych przez nią komórek i ośmiu sąsiadów, z wyjątkiem sytuacji, gdy komórki te są podzielone na cztery z jednym stanem i pięć z drugim stanem, w którym to przypadku nową wartością komórki jest mniejszość, a nie większość. Szczegółowa dynamika tej reguły jest skomplikowana, w tym istnienie małych stabilnych struktur. Jednak w agregacie (kiedy zaczyna się od wszystkich komórek w losowych stanach) ma tendencję do tworzenia dużych obszarów komórek, które są w tym samym stanie, a granice między tymi regionami ewoluują zgodnie z przepływem skracania krzywych.

Budowa geodezji zamkniętej

Przepływ skracający krzywą można wykorzystać do udowodnienia nierówności izoperymetrycznej dla powierzchni, których krzywizna Gaussa jest funkcją nierosnącą odległości od początku , np . paraboloidy . Na takiej powierzchni gładki zwarty zbiór, który ma dowolny obszar i minimalny obwód dla tego obszaru, jest z konieczności kołem o środku w punkcie początkowym. Dowód stosuje przepływ skracający krzywą do dwóch krzywych, koła metrycznego i granicy dowolnego innego zbioru zwartego, i porównuje zmianę obwodu dwóch krzywych, ponieważ obie są zredukowane do punktu przez przepływ. Przepływ skracający krzywą można również wykorzystać do udowodnienia twierdzenia trzech geodezji , że każda gładka rozmaitość Riemanna, topologicznie równoważna sferze, ma trzy geodezyje, które tworzą proste krzywe zamknięte .

Powiązane przepływy

Inne przepływy geometryczne związane z przepływem skracającym krzywą obejmują następujące.

Do symulacji zachowania kryształów lub innych materiałów anizotropowych ważne są warianty przepływu skracającego krzywą, dla których prędkość przepływu zależy od orientacji krzywej, jak również od jej krzywizny. Jednym ze sposobów na zrobienie tego jest zdefiniowanie energii krzywej jako całki gładkiej funkcji $γ$ jej wektorów normalnych i utworzenie gradientu tej energii, zgodnie z którym normalna prędkość, z jaką płynie krzywa, jest proporcjonalna do anizotropowy analog krzywizny. Ten przepływ można symulować, dyskretyzując krzywą jako wielokąt. W eksperymentach numerycznych początkowe krzywe wydają się zbiegać do kształtu Wulffa dla $γ$ przed skurczeniem się do punktu. Alternatywnie, można dopuścić do przedostania się z krzywej prędkości $($ $θ$ $)$ $κ$ $+$ $b$ $($ $θ$ $)$ gdzie $κ$ jest (zwykle) krzywizny i i $b$ są gładkimi funkcjami orientacji $θ$ . Gdy $a$ $($ $θ$ $+$ $π$ $) =$ $a$ $($ $θ$ $)$ i $b$ $($ $θ$ $+$ $π$ $) = -$ $b$ $($ $θ$ $)$ (tak, że przepływ jest niezmienny przy odbiciu punktowym ), można wykazać, że wynikowy przepływ jest zgodny z zasadą unikania i analog twierdzenia Gage'a-Hamiltona-Graysona.
Krzywej skrócenie afinicznej przepływu najpierw zbadano przez Alvarez et al. (1993) oraz Sapiro i Tannenbaum (1993) . W tym przepływie normalna prędkość krzywej jest proporcjonalna do pierwiastka sześciennego krzywizny. Wynikowy przepływ jest niezmienny (z odpowiednim skalowaniem czasu) pod transformacjami afinicznymi płaszczyzny euklidesowej, większą grupą symetrii niż transformacje podobieństwa, w których przepływ skracający krzywą jest niezmienny. W tym przepływie stosuje się analogię twierdzenia Gage-Hamiltona-Graysona, zgodnie z którym każda prosta zamknięta krzywa ostatecznie staje się wypukła, a następnie zbiega się do elipsy, gdy zapada się do punktu.
Przekształcenie krzywej z jednakowymi prędkościami normalnymi we wszystkich punktach zostało nazwane transformacją pożaru trawy . Krzywe wyewoluowane w ten sposób będą na ogół tworzyć ostre narożniki, których ślad tworzy środkową oś krzywej. Ściśle powiązana ewolucja krzywej, która przesuwa proste segmenty krzywej wielokątnej z jednakowymi prędkościami, ale pozwala wklęsłym narożnikom poruszać się szybciej niż prędkość jednostkowa, zamiast tego tworzy inny typ topologicznego szkieletu danej krzywej, jej prosty szkielet .
W przypadku powierzchni o wyższych wymiarach istnieje więcej niż jedna definicja krzywizny, w tym miary zewnętrzne (zależne od osadzenia), takie jak średnia krzywizna i miary wewnętrzne, takie jak krzywizna skalarna i krzywizna Ricciego . Odpowiednio, istnieje kilka sposobów definiowania przepływów geometrycznych opartych na krzywiźnie, w tym przepływ średniej krzywizny (w którym normalna prędkość osadzonej powierzchni jest jej średnią krzywizną), przepływ Ricciego (przepływ wewnętrzny na metryce przestrzeni opartej na jego krzywiznę Ricciego), przepływ krzywizny Gaussa i przepływ Willmore'a (przepływ gradientowy dla funkcjonału energetycznego łączącego średnią krzywiznę i krzywiznę Gaussa). Przepływ skracający krzywą jest szczególnym przypadkiem przepływu średniej krzywizny i przepływu krzywizny Gaussa dla krzywych jednowymiarowych.
Zainspirowani przepływem skracającym krzywą na gładkich krzywych, naukowcy zbadali metody płynących wielokątów, tak aby pozostawały wielokątne, przy zastosowaniu takich zastosowań, jak tworzenie wzorców i synchronizacja w rozproszonych systemach robotów. Przepływy wielokątne zachowujące długość można wykorzystać do rozwiązania problemu reguły cieśli .
W widzenia komputerowego The aktywny wzór konturu dla wykrywania krawędzi i segmentacji obrazu jest oparty na krzywej skracania i rozwija krzywe oparte na kombinacji ich krzywizny i cech obrazu.

Uwagi

Bibliografia

Abresch, U.; Langer, J. (1986), „Krzywa znormalizowana skracanie przepływu i rozwiązania homotetyczne”, Journal of Differential Geometry , 23 (2): 175-196, doi : 10.4310/jdg/1214440025 , MR 0845704.
Aichholzera, Oswina; Aurenhammer, Franz ; Albertowie, David; Gärtner, Bernd (1995), „Nowy typ szkieletu dla wielokątów” , Journal of Universal Computer Science , 1 (12): 752–761, CiteSeerX 10.1.1.135.9800 , doi : 10.1007/978-3-642-80350 -5_65 , MR 1392429.
Altschuler, Steven J. (1991), „Singularities of the curve kurczenie się przepływu dla krzywych przestrzennych”, Journal of Differential Geometry , 34 (2): 491-514, doi : 10.4310/jdg/1214447218 , MR 1131441.
Altschuler, Dylan J.; Altschuler, Steven J.; Angenent, Sigurd B .; Wu, Lani F. (2013), „Zoo solitonów do skracania krzywej w ”, Nieliniowość , 26 (5): 1189–1226, arXiv : 1207.4051 , Bibcode : 2013Nonli..26.1189A , doi : 10.1088/0951-7715 /26/5/1189 , MR 3043378 , S2CID 1959710 ${\ Displaystyle \ mathbb {R} ^ {n}}$ .
Altschuler, Steven J.; Grayson, Matthew A. (1992), „Skrócenie krzywych przestrzennych i przepływ przez osobliwości”, Journal of Differential Geometry , 35 (2): 283-298, doi : 10.4310/jdg/1214448076 , MR 1158337.
Alvarez, Luis; Guichard, Fryderyk; Lwy, Pierre-Louis; Morel, Jean-Michel (1993), „Aksjomaty i podstawowe równania przetwarzania obrazu”, Archive for Rational Mechanics and Analysis , 123 (3): 199-257, Bibcode : 1993ArRMA.123..199A , doi : 10.1007/BF00375127 , MR 1225209 , S2CID 121702431.
Andrewsa, Bena; Bryan, Paul (2011), „Krzywa ograniczona do krzywej skracania przepływu poprzez porównanie odległości i bezpośredni dowód twierdzenia Graysona”, Journal für die Reine und Angewandte Mathematik , 2011 (653): 179-187, arXiv : 0908.2682 , doi : 10.1515 /CRELLE.2011.026 , MR 2794630 , S2CID 16124939.
Angenent, Sigurd (1991a), „Równania paraboliczne dla krzywych na powierzchniach. II. Przecięcia, upadki i rozwiązania uogólnione”, Annals of Mathematics , Druga seria, 133 (1): 171-215, doi : 10.2307/2944327 , JSTOR 2944327 , MR 1087347.
Angenent, Sigurd (1991b), „O tworzeniu osobliwości w krzywej skracania przepływu”, Journal of Differential Geometry , 33 (3): 601-633, doi : 10.4310/jdg/1214446558 , MR 1100205.
Angenent, Sigurd B. (1992), "Kurczenie pączków" (PDF) , Nieliniowe równania dyfuzji i ich stany równowagi, 3 (Gregynog, 1989) , Postęp w nieliniowych równaniach różniczkowych i ich zastosowania, 7 , Boston, MA: Birkhäuser, s. 21-38, MR 1167827.
Angenent, S. (1999), "Punkty przegięcia, punkty eksttyczne i skrócenie krzywej" (PDF) , systemy hamiltonowskie z trzema lub więcej stopniami swobody (S'Agaró, 1995) , NATO Adv. Nauka. Inst. Ser. Matematyka. Fiz. Sci., 533 , Dordrecht: Kluwer Acad. Publ., s. 3–10, MR 1720878
Angenent, Sigurd ; Sapiro, Guillermo ; Tannenbaum, Allen (1998), „Na afinicznym równaniu ciepła dla krzywych niewypukłych ”, Journal of the American Mathematical Society , 11 (3): 601-634, doi : 10.1090/S0894-0347-98-00262-8 , MR 1491538.
Au, Thomas Kwok-Keung (2010), „O właściwości punktu siodłowego krzywych Abrescha-Langera pod krzywą skracającą przepływ”, Communications in Analysis and Geometry , 18 (1): 1-21, arXiv : math/0102088 , doi : 10.4310/CAG.2010.v18.n1.a1 , MR 2660456 , S2CID 16046863.
Balažovjech, Martin; Mikula, Karol (2009), „Schemat wyższego rzędu dla krzywej skracającej przepływ krzywych płaskich” (PDF) , Algoritmy 2009 , s. 165–175.
Barrett, John W.; Garcke, Harald; Nürnberg, Robert (2011), „Aproksymacja ewolucji krzywych planarnych przez stabilne, w pełni niejawne schematy elementów skończonych, które są równodystrybuowane” (PDF) , Metody numeryczne dla równań różniczkowych cząstkowych , 27 : 1-30, doi : 10.1002/num.20637 , MR 2743598.
Bellettini, Giovanni; Novaga, Matteo (2011), "Ewolucja krzywizny niewypukłych domen w kształcie soczewki", Journal für die Reine und Angewandte Mathematik , 2011 (656): 17-46, arXiv : 0906.0166 , doi : 10.1515/CRELLE.2011.041 , MR 2818854 , S2CID 14158286.
Benjamini, Włochy ; Cao, Jianguo (1996), „Nowe twierdzenie o porównaniu izoperymetrycznym dla powierzchni o zmiennej krzywiźnie”, Duke Mathematical Journal , 85 (2): 359-396, doi : 10.1215/S0012-7094-96-08515-4 , MR 1417620.
Brakke, Kenneth A. (1978), Ruch powierzchni przez jej średnią krzywiznę (PDF) , Uwagi matematyczne, 20 , Princeton University Press, Princeton, NJ, ISBN 0-691-08204-9, MR 0485012.
Bourni, Teodora; Langford, Mat; Tinaglia, Giuseppe (2020), "Wypukłe starożytne rozwiązania do krzywej skracania przepływu", Rachunek wariacyjny i objętości równań różniczkowych cząstkowych , 133 (59): 15, doi : 10.1007/s00526-020-01784-8 , MR 4127403.
Broadbridge, Filip; Vassiliou, Peter (2011), "Rola symetrii i separacji w ewolucji powierzchni i skracaniu krzywej", SIGMA , 7 : Paper 052, 19, arXiv : 1106.0092 , Bibcode : 2011SIGMA...7..052B , doi : 10.3842/ SIGMA.2011.052 , MR 2804584 , S2CID 8998552.
Brook, Aleksander; Bruckstein, Alfred M.; Kimmel, Ron (2005), "O niezmiennych miarach uczciwości podobieństwa", w Kimmel, Ron ; Sochen, Nir A.; Weickert, Joachim (red.), Scale Space and PDE Methods in Computer Vision: 5. Międzynarodowa Konferencja, Scale-Space 2005, Hofgeismar, Niemcy, 7-9 kwietnia 2005, Proceedings , Lecture Notes in Computer Science, 3459 , Springer-Verlag , s. 456–467, CiteSeerX 10.1.1.67.1807 , doi : 10.1007/11408031_39.
Bryant, Robert L .; Griffiths, Phillip A. (1995), „Charakterystyczna kohomologia układów różniczkowych. II. Prawa zachowania dla klasy równań parabolicznych”, Duke Mathematical Journal , 78 (3): 531-676, doi : 10.1215/S0012-7094-95 -07824-7 , MR 1334205. Patrz w szczególności Przykład 1, s. 542-544 i 601-604.
Cantarella, Jason H.; Demaine, Erik D .; Iben, Hayley N.; O'Brien, James F. (2004), „An energy-driven approach to linkage unfolding”, Proceedings of the Twentieth Annual Symposium on Computational Geometry (SCG '04) , Nowy Jork, NY, USA: ACM, s. 134- 143, CiteSeerX 10.1.1.1001.9683 , doi : 10.1145/997817.997840 , ISBN 1-58113-885-7, S2CID 6694097.
Cao, Frédéric (2003), Ewolucja krzywej geometrycznej i przetwarzanie obrazu , Notatki do wykładu z matematyki, 1805 , Berlin: Springer-Verlag, doi : 10.1007/b10404 , ISBN 3-540-00402-5, MR 1976551.
Chopard, Bastien; Droz, Michel (1998), "2.2.4 Zasada wyżarzania" Komórkowy automaty modelowanie układów fizycznych , Kolekcja Alea-Saclay: Monografie i Teksty w fizyce statystycznej, Cambridge University Press, Cambridge, pp 37-38,. Doi : 10,1017 /CBO9780511549755 , ISBN 0-521-46168-5, MR 1669736.
Chou, Kai-Seng; Zhu, Xi-Ping (1998), „Shortening complete plane curves”, Journal of Differential Geometry , 50 (3): 471-504, doi : 10.4310/jdg/1214424967 , MR 1690737.
Chou, Kai-Seng; Zhu, Xi-Ping (2001), Problem skracania krzywej , Boca Raton, FL: Chapman & Hall / CRC, doi : 10.1201/9781420035704 , ISBN 1-58488-213-1, MR 1888641.
Crandall, Michael G.; Lions, Pierre-Louis (1996), „Zbieżne schematy różnicowe dla nieliniowych równań parabolicznych i średniej krzywizny ruchu”, Numerische Mathematik , 75 (1): 17-41, doi : 10.1007/s002110050228 , MR 1417861 , S2CID 119792668.
Daskalopoulos, Panagiota ; Hamilton, Richard ; Sesum, Natasa (2010), „Classification of compact ancient solutions to curve shortening flow”, Journal of Differential Geometry , 84 (3): 455–464, arXiv : 0806.1757 , doi : 10.4310/jdg/1279114297 , MR 2669361 , S2CID 18747005.
Deckelnick, Klaus (2000), „Granice błędu dla schematu różnicowego przybliżającego roztwory lepkości o średniej krzywiźnie przepływu”, Interfejsy i swobodne granice , 2 (2): 117-142, doi : 10.4171/IFB/15 , MR 1760409.
Deckelnick, K.; Dziuk, G. (1995), „O aproksymacji krzywej skracania przepływu”, Rachunek wariacyjny, zastosowania i obliczenia (Pont-à-Mousson, 1994) , Pitman Res. Uwagi Matematyka. Ser., 326 , Longman Sci. Tech., Harlow, s. 100–108, MR 1419337.
Devadoss, Satyan L .; O'Rourke, Joseph (2011), "5,5 skracanie krzywej", Geometria dyskretna i obliczeniowa , Princeton, NJ: Princeton University Press, s. 138-144, ISBN 978-0-691-14553-2, MR 2790764.
Dziuk, Gerhard (1999), „Discrete anisotropic curve skracanie przepływu”, SIAM Journal on Numerical Analysis , 36 (6): 1808–1830, doi : 10.1137/S0036142998337533 , MR 1712165.
Elliotta, Karola M.; Fritz, Hans (2017), „O przybliżeniach krzywej skracania przepływu i średniego przepływu krzywizny w oparciu o sztuczkę DeTurcka”, IMA Journal of Numerical Analysis , 37 (2): 543-603, arXiv : 1602.07143 , doi : 10.1093 /imanum/drw020 , MR 3649420.
Epsteina, CL ; Weinstein, MI (1987), „Stabilne twierdzenie o rozmaitości dla równania skracania krzywej”, Communications on Pure and Applied Mathematics , 40 (1): 119-139, doi : 10.1002/cpa.3160400106 , MR 0865360.
Esedoglu, Selim; Ruth, Steven; Tsai, Richard (2010), „Ruch generowany dyfuzją przy użyciu funkcji odległości ze znakiem ” (PDF) , Journal of Computational Physics , 229 (4): 1017-1042, Bibcode : 2010JCoPh.229.1017E , doi : 10.1016/j.jcp.2009.10 0,002 , MR 2576237.
Gage, Michael E. (1983), „Nierówność izoperymetryczna z zastosowaniami do skracania krzywej”, Duke Mathematical Journal , 50 (4): 1225-1229, doi : 10.1215/S0012-7094-83-05052-4 , MR 0726325.
Gage, ME (1984), "Curve shortening sprawia, że krzywe wypukłe są kołowe", Inventiones Mathematicae , 76 (2): 357-364, Bibcode : 1984InMat..76..357G , doi : 10.1007/BF01388602 , MR 0742856 , S2CID 121981987.
Gage, M .; Hamilton, RS (1986), „Równanie ciepła kurczące się wypukłe krzywe płaszczyzny”, Journal of Differential Geometry , 23 (1): 69-96, doi : 10.4310/jdg/1214439902 , MR 0840401.
Grayson, Matthew A. (1987), „Równanie ciepła kurczy osadzone krzywe płaszczyzny do okrągłych punktów”, Journal of Differential Geometry , 26 (2): 285-314, doi : 10.4310/jdg/1214441371 , MR 0906392.
Grayson, Matthew A. (1989a), „Kształt ósemki pod krzywą skracającą przepływ” , Inventiones Mathematicae , 96 (1): 177-180, Bibcode : 1989InMat..96..177G , doi : 10.1007/ BF01393973 , MR 0981740 , S2CID 120965191.
Grayson, Matthew A. (1989b), "Skrócenie wbudowanych krzywych" (PDF) , Annals of Mathematics , Druga seria, 129 (1): 71-111, doi : 10.2307/1971486 , JSTOR 1971486 , MR 0979601.
Halldórsson, Höskuldur P. (2012), "Samopodobne rozwiązania do krzywej skracania przepływu", Transactions of the American Mathematical Society , 364 (10): 5285-5309, arXiv : 1007.1617 , doi : 10.1090/S0002-9947-2012 -05632-7 , MR 2931330 , S2CID 54018685.
Hausser, Frank; Voigt, Axel (2006), „Schemat numeryczny skracania przepływu uregulowanej krzywej anizotropowej”, Applied Mathematics Letters , 19 (8): 691-698, doi : 10.1016/j.aml.2005.05.011 , MR 2232241.
Holden, Helge; Risebro, Nils Henrik (2015), Front Tracking for Hyperbolic Conservation Laws , Applied Mathematical Sciences, 152 (2nd ed.), Springer, ISBN 978-3-662-47507-2.
Huisken, Gerhard (1990), „Asymptotyczne zachowanie dla osobliwości średniego przepływu krzywizny”, Journal of Differential Geometry , 31 (1): 285-299, doi : 10.4310/jdg/1214444099 , MR 1030675.
Huisken, Gerhard (1998), „Zasada porównania odległości dla ewoluujących krzywych”, The Asian Journal of Mathematics , 2 (1): 127-133, doi : 10.4310/ajm.1998.v2.n1.a2 , MR 1656553.
Huisken, Gerhard ; Sinestrari, Carlo (2015), „Wypukłe starożytne rozwiązania przepływu średniej krzywizny”, Journal of Differential Geometry , 101 (2): 267-287, arXiv : 1405.7509 , doi : 10.4310/jdg/1442364652 , MR 3399098 , S2CID 119129510.
Ilmanen, Tom (1994), „Regularyzacja eliptyczna i częściowa regularność ruchu przez średnią krzywiznę”, Memoirs of the American Mathematical Society , 108 (520), doi : 10.1090/memo/0520 , MR 1196160.
Ilmanen, Tom; Neves, André ; Schulze, Felix (2014), O krótkim czasie istnienia dla płaskiego przepływu sieci , arXiv : 1407.4756 , Bibcode : 2014arXiv1407.4756I.
Ishimura, Naoyuki (1995), „Ewolucja krzywizny krzywych płaskich z określonym kątem otwarcia”, Biuletyn Australijskiego Towarzystwa Matematycznego , 52 (2): 287-296, doi : 10.1017/S0004972700014714 , MR 1348488.
Kichenassamy, S.; Kumar, A.; Olver, P .; Tannenbauma, A .; Yezzi, A. (1995), „Przepływy gradientowe i geometryczne aktywne modele konturowe”, Proceedings of IEEE International Conference on Computer Vision , s. 810-815, CiteSeerX 10.1.1.331.675 , doi : 10.1109/iccv.1995.466855 , S2CID 10355426.
Kimmel, Ron (2004), Numeryczna geometria obrazów: teoria, algorytmy i zastosowania , Springer-Verlag, ISBN 978-0-387-21637-9, MR 2028182.
Kimura, M. (1994), „Dokładny schemat numeryczny dla przepływu przez krzywiznę”, Applied Mathematics Letters , 7 (1): 69-73, doi : 10.1016/0893-9659 (94) 90056-6 , MR 1349897.
Lam, Casey; Lauer, Joseph (2016), Poziomowy przepływ krzywej sinusoidalnej topologa jest gładki , arXiv : 1601.02442 , Bibcode : 2016arXiv160102442L
Lauer, Joseph (2013), „Nowa ocena długości krzywej skracania przepływu i danych początkowych o niskiej regularności”, Analiza geometryczna i funkcjonalna , 23 (6): 1934-1961, arXiv : 1102.5110 , doi : 10.1007/s00039-013-0248 -1 , MR 3132906 , S2CID 119339054.
Łukjanow, SL; Wiczew, ES; Zamolodchikov, AB (2004), "Integrowalny model interakcji granic: spinacz", Nuclear Physics B , 683 (3): 423-454, arXiv : hep-th/0312168 , Bibcode : 2004NuPhB.683..423L , doi : 10.1016/j.nuclphysb.2004.02.010 , S2CID 119124585.
Merrimana, Barry'ego; Bence, Jakubie; Osher, Stanley (kwiecień 1992), Ruch generowany przez dyfuzję przez średnią krzywiznę (PDF) , Raport CAM 92-18, Wydział Matematyki, Uniwersytet Kalifornijski, Los Angeles. Opublikowano również w Taylor, Jean E. (1992), Computational Crystal Growers Workshop: Proceedings of the Geometry Center Workshop, które odbyło się w Minneapolis, Minnesota, 22–28 lutego 1992 , Selected Lectures in Mathematics, Providence, RI: American Mathematical Society, s. 73-83, ISBN 0-8218-8072-1, MR 1224451.
Mikuła, Karol; Ševčovič, Daniel (1999), "Rozwiązanie nieliniowej krzywizny napędzanej ewolucji krzywych płaskich", Applied Numerical Mathematics , 31 (2): 191-207, doi : 10.1016/S0168-9274 (98) 00130-5 , MR 1708959.
Mikuła, Karol; Ševčovič, Daniel (2001), „Ewolucja krzywych płaskich sterowanych nieliniową funkcją krzywizny i anizotropii”, SIAM Journal on Applied Mathematics , 61 (5): 1473–1501 (elektroniczny), CiteSeerX 10.1.1.32.1138 , doi : 10.1137/S0036139999359288 , MR 1824511.
Minarčík, Jiří; Beneš, Michal (2020), „Długoterminowe zachowanie krzywej skracania przepływu w ”, SIAM Journal on Mathematical Analysis , 52 (2): 1221–1231, doi : 10.1137/19M1248522 , MR 4076813 ${\ Displaystyle \ mathbb {R} ^ {3}}$ .
Mokhtarian, F.; Mackworth, AK (1992), „Teoria wieloskalowej, opartej na krzywiźnie reprezentacji kształtu dla krzywych planarnych” (PDF) , IEEE Transactions on Pattern Analysis and Machine Intelligence , 14 (8): 789-805, doi : 10.1109/34.149591.
Mullins, WW (1956), "Dwuwymiarowy ruch wyidealizowanych granic ziaren", Journal of Applied Physics , 27 (8): 900-904, Bibcode : 1956JAP .... 27..900M , doi : 10.1063/1.1722511. Przedruk w Ball, John M .; Kinderlehrer, Dawid ; Podio-Guidugli, Paulo; Slemrod, Marshall, wyd. (1999), Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids: A Collection of Reprints of 14 Seminal Papers , Springer-Verlag, s. 70-74, doi : 10.1007/978-3-642-59938-5_3 , Numer ISBN 978-3-642-59938-5.
Pickover, Clifford A. (1993), „lampy lawowe w XXI wieku”, The Visual Computer , 10 (3): 173-177, doi : 10.1007/bf01900906 , S2CID 29417478.
Rens, Fryderyk N.; Craig, Kenneth R.; DeHoff, Robert T. (1974), "Mechanizm stacjonarnego wzrostu ziarna w aluminium", Metallurgical Transactions , 5 (2): 413-425, Bibcode : 1974MT......5..413R , doi : 10.1007 /bf02644109 , S2CID 136991523.
Ritoré, Manuel; Sinestrari, Carlo (2010), „2.2 Curve shortening flow” , Mean Curvature Flow and Isperimetric Inequalities , Advanced Courses in Mathematics – CRM Barcelona, Birkhäuser, s. 72–75, doi : 10.1007/978-3-0346-0213-6_13 , ISBN 978-3-0346-0213-6.
Rubinstein, Jakub; Sternberg, Piotr; Keller, Joseph B. (1989), „Szybka reakcja, powolna dyfuzja i skrócenie krzywej”, SIAM Journal on Applied Mathematics , 49 (1): 116-133, doi : 10.1137/0149007 , MR 0978829.
Sapiro, Guillermo ; Tannenbaum, Allen (1993), "Affine niezmiennicza przestrzeń skali", International Journal of Computer Vision , 11 (1): 25-44, doi : 10.1007/bf01420591 , S2CID 13163111.
Schnürer, Oliver C.; Azouani, Abderrahim; Georgi, Marc; Piekło, Juliette; Dżangle, Nihar; Koellera, Amosa; Marksena, Tobiasza; Ritthaler, Sandra; Saez, Mariel; Schulze, Feliks; Smith, Brian (2011), „Ewolucja sieci wypukłych w kształcie soczewki pod krzywą skracania przepływu”, Transactions of the American Mathematical Society , 363 (5): 2265-2294, arXiv : 0711.1108 , doi : 10.1090/S0002-9947- 2010-04820-2 , MR 2763716 , S2CID 16595310.
Scriven, LE (1960), „Dynamika interfejsu płynu Równanie ruchu dla płynów powierzchniowych Newtona”, Chemical Engineering Science , 12 (2): 98-108, doi : 10.1016/0009-2509 (60) 87003-0.
Smith, Stephen L.; Broucke, Mireille E .; Francis, Bruce A. (2007), „Curve shortening and the rendez-vous problem for mobile autonomi robots”, IEEE Transactions on Automatic Control , 52 (6): 1154–1159, arXiv : cs/0605070 , doi : 10.1109/tac.2007.899024 , S2CID 574140.
Vichniac, Gérard Y. (1986), "Modele automatów komórkowych zaburzeń i organizacji", w Bienenstock, E.; Fogelman Soulie, F.; Weisbuch, G. (red.), Disordered Systems and Biological Organization , NATO ASI Series, 20 , Springer-Verlag, s. 3-20, doi : 10.1007/978-3-642-82657-3_1.
White, Brian (1989), „Niektóre najnowsze osiągnięcia w geometrii różniczkowej”, The Mathematical Intelligencer , 11 (4): 41-47, doi : 10.1007/BF03025885 , MR 1016106 , S2CID 122335761.
White, Brian (2002), "Ewolucja krzywych i powierzchni przez średnią krzywiznę", Proceedings of the International Congress of Mathematicians, tom. I (Pekin, 2002) , wyd. Prasa, Pekin, s. 525–538, arXiv : math/0212407 , Bibcode : 2002math.....12407W , MR 1989203.
Ty, Qian (2014), Some Ancient Solutions of Curve Shortening , Ph.D. praca dyplomowa, The University of Wisconsin – Madison, ProQuest 1641120538.

Languages

In other projects