Tetracja - Tetration

W matematyce , tetracja (lub hiper-4 ), to działanie na podstawie powtarzanych lub powtórzono potęgowanie . Jest to kolejna hiperoperacja po potęgowaniu , ale przed pentacją . Słowo zostało ukute przez Reubena Louisa Goodsteina z tetra- (cztery) i iteracji .

Zgodnie z definicją jako powtarzane potęgowanie, notacja Rudy'ego Ruckera oznacza , gdzie n kopii a jest iterowanych przez potęgowanie, od prawej do lewej, tj. zastosowanie czasów potęgowania . n jest nazywane „wysokość” funkcji, podczas gdy a jest nazywane „podstawą”, analogicznie do potęgowania. Byłoby to odczytywane jako „ n- ta tetracja a ”. ${\ Displaystyle {^ {n} a}}$${\ Displaystyle {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}}}$${\displaystyle n-1}$

Tetracja jest również definiowana rekurencyjnie jako

${\ Displaystyle {^ {n} a}: = {\ zacząć {przypadki} 1 i {\ tekst {jeśli}} n = 0 \ \ a ^ {\ lewo (^ {(n-1)} a \ prawej)} &{\text{if }}n>0\end{przypadków}}}$,

pozwalając na próby rozszerzenia tetracji na liczby nienaturalne, takie jak liczby rzeczywiste i zespolone.

Te dwie odwrotności tetracji nazywane są super pierwiastkiem i super-logarytmem , analogicznie do pierwiastka n-tego i funkcji logarytmicznych. Żadna z trzech funkcji nie jest elementarna .

Tetracja służy do notacji bardzo dużych liczb .

Wstęp

Tutaj pokazane są pierwsze cztery hiperoperacje , przy czym tetracja jest uważana za czwartą w serii. Jednoargumentowy działanie następstwo zdefiniowany jako jest uważany za zerowe działanie. ${\displaystyle a'=a+1}$

1. Dodatek

   ${\ Displaystyle a + n = a + \ underbrace {1 + 1 + \ cdots +1} _ {n}}$

   n kopie 1 dodano do .

2. Mnożenie

   ${\ Displaystyle a \ razy n = \ underbrace {a + a + \ cdots + a} _ {n}}$

   n kopiepołączone przez dodatek.

3. Potęgowanie

   ${\ Displaystyle a ^ {n} = \ underbrace {a \ raz za \ raz \ cdots \ raz za} _ {n}}$

   n kopiepołączone przez mnożenie.

4. Tetracja

   ${\ Displaystyle {^ {n} a} = \ underbrace {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}} _ {n}}$

   n kopiepołączone przez potęgowania, od prawej do lewej.

Dziedziczenie ( a′ = a + 1) , jest najbardziej podstawową operacją; podczas gdy dodawanie ( a + n ) jest operacją pierwotną , dla dodawania liczb naturalnych można je traktować jako łańcuchowe następstwo n następców a ; mnożenie ( a  ×  n ) jest również operacją podstawową, chociaż w przypadku liczb naturalnych można ją analogicznie traktować jako dodawanie łańcuchowe obejmujące n liczb a . Potęgowanie można traktować jako łańcuchowe mnożenie obejmujące n liczb a i tetrację ( ) jako łańcuchową potęgę obejmującą n liczb a . Każda z powyższych operacji jest definiowana przez iterację poprzedniej; jednak w przeciwieństwie do operacji przed nim tetracja nie jest funkcją elementarną . ${\ Displaystyle ^ {n} a \!}$

Parametr a to podstawa , a parametr n to wysokość . W pierwotnej definicji tetracji parametr wysokości musi być liczbą naturalną; na przykład nielogiczne byłoby powiedzenie „trzech podniosło się do siebie pięć razy negatywnych” lub „czterech podniosło się do siebie po połowie czasu”. Jednak podobnie jak dodawanie, mnożenie i potęgowanie można zdefiniować w sposób, który pozwala na rozszerzenia do liczb rzeczywistych i zespolonych, podjęto kilka prób uogólnienia tetracji na liczby ujemne, liczby rzeczywiste i liczby zespolone. Jednym z takich sposobów jest użycie rekurencyjnej definicji tetracji; dla dowolnej dodatniej liczby całkowitej rzeczywistej i nieujemnej możemy zdefiniować rekurencyjnie jako: ${\displaystyle a>0}$ ${\displaystyle n\geq 0}$${\ Displaystyle \ \! {^ {n} a}}$

${\ Displaystyle {^ {n} a}: = {\ zacząć {przypadki} 1 i {\ tekst {jeśli}} n = 0 \ \ a ^ {\ lewo (^ {(n-1)} a \ prawej)} &{\text{if }}n>0\end{przypadków}}}$

Definicja rekurencyjna jest równoważna powtarzanej potęgi dla naturalnych wysokości; jednak ta definicja pozwala na rozszerzenia do innych wysokości, takich jak , , a także – wiele z tych rozszerzeń to obszary aktywnych badań. ${\displaystyle ^{0}a}$${\ Displaystyle ^ {-1} a}$${\ Displaystyle ^ {i} a}$

Terminologia

Istnieje wiele terminów na tetrację, z których każdy ma jakąś logikę, ale niektóre nie są powszechnie używane z tego czy innego powodu. Oto porównanie każdego terminu z jego uzasadnieniem i kontrracjonalnością.

• Dominuje termin tetracja , wprowadzony przez Goodsteina w jego pracy z 1947 r. Transfinite Ordinals in Recursive Number Theory (uogólniający rekurencyjną reprezentację bazy używaną w twierdzeniu Goodsteina do stosowania wyższych operacji). Stwierdzono także spopularyzował w Rudy Rucker „s nieskończoności i umysł .
• Termin superpotęgowanie został opublikowany przez Bromera w jego artykule Superpotęgowanie w 1987 roku. Został użyty wcześniej przez Eda Nelsona w jego książce Predicative Arithmetic, Princeton University Press, 1986.
• Termin hipermoc jest naturalną kombinacją hiper i mocy , która trafnie opisuje tetrację. Problem tkwi w znaczeniu hiper w odniesieniu do sekwencji hiperoperacji . Rozważając hiperoperacje, termin hiper odnosi się do wszystkich rang, a termin super odnosi się do rang 4 lub tetracji. Tak więc w tych rozważaniach hipermoc jest myląca, ponieważ odnosi się tylko do tetracji.
• Termin „ wieża mocy” jest czasami używany w postaci „wieża mocy rzędu n ” dla . Jest to jednak błędna nazwa, ponieważ tetracji nie można wyrazić za pomocą iterowanych funkcji potęgowych (patrz wyżej), ponieważ jest to iterowana funkcja wykładnicza .${\ Displaystyle {\ \ atop {\ }} {\ underbrace {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}}} \ atop n}}$

Częściowo z powodu pewnej wspólnej terminologii i podobnej symboliki notacji , tetracja jest często mylona z blisko powiązanymi funkcjami i wyrażeniami. Oto kilka powiązanych terminów:

Terminy związane z tetracją

Terminologia	Formularz
Tetracja	${\ Displaystyle a ^ {a ^ {\ cdot ^ {\ cdot ^ {a ^ {a}}}}}}$
Iterowane wykładniki	${\ Displaystyle a ^ {a ^ {\ cdot ^ {\ cdot ^ {a ^ {x}}}}}}$
Zagnieżdżone wykładniki (również wieże)	${\ Displaystyle a_ {1} ^ {a_ {2} ^ {\ cdot ^ {\ cdot ^ {a_ {n}}}}}}$
Nieskończone wykładniki (również wieże)	${\ Displaystyle a_ {1} ^ {a_ {2} ^ {a_ {3} ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}}}}$

W pierwszych dwóch wyrażeniach a jest podstawą , a liczba wystąpień a jest wysokością (dodaj jeden dla x ). W trzecim wyrażeniu n to wysokość , ale każda z podstaw jest inna.

Należy zachować ostrożność podczas odwoływania się do iterowanych wykładników, ponieważ często nazywa się wyrażenia tej formy iterowaną potęgą, co jest niejednoznaczne, ponieważ może to oznaczać albo iterowane potęgi, albo iterowane wykładniki .

Notacja

Istnieje wiele różnych stylów notacji, których można użyć do wyrażenia tetracji. Niektóre zapisy mogą być również użyte do opisania innych hiperoperacji , podczas gdy niektóre są ograniczone do tetracji i nie mają natychmiastowego rozszerzenia.

Style notacji dla tetracji

Nazwa	Formularz	Opis
Notacja Rudy'ego Ruckera	${\ Displaystyle \, {} ^ {n} a}$	Używany przez Maurera [1901] i Goodsteina [1947]; Notację spopularyzowała książka Rudy'ego Ruckera Infinity and the Mind .
Notacja Knutha ze strzałką w górę	${\displaystyle a{\uparrow \uparrow}n}$	Umożliwia rozszerzenie poprzez umieszczenie większej liczby strzał lub, jeszcze mocniej, strzałki indeksowanej.
Notacja ze strzałką w łańcuchu Conwaya	${\displaystyle a\rightarrow n\rightarrow 2}$	Umożliwia wydłużenie poprzez zwiększenie liczby 2 (odpowiednik rozszerzeń powyżej), ale także, jeszcze mocniej, poprzez wydłużenie łańcucha
Funkcja Ackermanna	${\ Displaystyle {} ^ {n} 2 = \ nazwa operatora {A} (4, n-3) + 3}$	Umożliwia zapisanie szczególnego przypadku w odniesieniu do funkcji Ackermanna. ${\displaystyle a=2}$
Iterowana notacja wykładnicza	${\ Displaystyle \ exp _ {a} ^ {n} (1)}$	Umożliwia proste rozszerzenie do iterowanych wykładników od wartości początkowych innych niż 1.
Notacje Hooshmanda	${\ Displaystyle {\ zacząć {wyrównany} i \ operatorname {uxp} _ {a} n \ \ [2 pkt] i a ^ {\ Frac {n}} \ koniec {wyrównany}}}$	Używany przez MH Hooshmanda [2006].
Hyperoperation notacje	${\ Displaystyle {\ zacząć {wyrównany} i a [4] n \ \ [2 pkt] i H_ {4} (a, n) \ koniec {wyrównany}}}$	Umożliwia rozszerzenie poprzez zwiększenie liczby 4; to daje rodzinę hiperoperacji .
Notacja podwójna karetka	a^^n	Ponieważ strzałka w górę jest używana identycznie jak karetka ( ^), tetracja może być zapisana jako ( ^^); wygodny dla ASCII .

Jedna z powyższych notacji używa iterowanej notacji wykładniczej; definiuje się to ogólnie w następujący sposób:

${\ Displaystyle \ exp _ {a} ^ {n} (x) = a ^ {a ^ {\ cdot ^ {\ cdot ^ {a ^ {x}}}}}$z n za s.

Nie ma tak wielu notacji dla iterowanych wykładników, ale oto kilka:

Style notacji dla iterowanych wykładników

Nazwa	Formularz	Opis
Notacja standardowa	${\ Displaystyle \ exp _ {a} ^ {n} (x)}$	Euler ukuł notację , a notacja iteracyjna istnieje mniej więcej tak długo. ${\ Displaystyle \ exp _ {a} (x) = a ^ {x}}$${\ Displaystyle f ^ {n} (x)}$
Notacja Knutha ze strzałką w górę	${\ Displaystyle (a {\ uparrow}) ^ {n} (x)}$	Pozwala na supermoce i funkcję super-wykładniczą poprzez zwiększenie liczby strzał; używane w artykule na temat dużych liczb .
Notacja tekstowa	exp_a^n(x)	Na podstawie standardowej notacji; wygodny dla ASCII .
Notacja J	x^^:(n-1)x	Powtarza potęgowanie. Zobacz J (język programowania)

Przykłady

Ze względu na niezwykle szybki wzrost tetracji większość wartości w poniższej tabeli jest zbyt duża, aby można je było zapisać w notacji naukowej. W takich przypadkach do wyrażenia ich o podstawie 10 stosuje się iterowany zapis wykładniczy. Wartości zawierające kropkę dziesiętną są przybliżone.

Przykłady tetracja

${\displaystyle x}$	${\displaystyle {}^{2}x}$	${\ Displaystyle {} ^ {3}x}$	${\ Displaystyle {} ^ {4}x}$	${\ Displaystyle {} ^ {5} x}$
1	1	1	1	1
2	4	16	65 536	2 65536 lub (2,0035 x 10 19728 )
3	27	7 625 597 484 987	${\ Displaystyle \ exp _ {10} ^ {3}(1.09902)}$(3,6 × 10 12 cyfr)	${\ Displaystyle \ exp _ {10} ^ {4}(1.09902)}$
4	256	1.34078 × 10 154	${\ Displaystyle \ exp _ {10} ^ {3}(2.18726)}$(8,1 × 10 153 cyfry)	${\ Displaystyle \ exp _ {10} ^ {4}(2.18726)}$
5	3125	1,91101 × 10 2184	${\ Displaystyle \ exp _ {10} ^ {3}(3.33928)}$(1,3 × 10 2184 cyfry)	${\ Displaystyle \ exp _ {10} ^ {4}(3.33928)}$
6	46,656	2,65912 × 10 36,305	${\ Displaystyle \ exp _ {10} ^ {3}(4.55997)}$(2,1 × 10 36 305 cyfr)	${\ Displaystyle \ exp _ {10} ^ {4}(4.55997)}$
7	823 543	3,75982 × 10 695 974	${\ Displaystyle \ exp _ {10} ^ {3}(5.84259)}$(3,2 × 10 695 974 cyfry)	${\ Displaystyle \ exp _ {10} ^ {4}(5.84259)}$
8	16 777 216	6,01452 × 10 15 151 335	${\ Displaystyle \ exp _ {10} ^ {3}(7.18045)}$(5,4 × 10 15 151 335 cyfr)	${\ Displaystyle \ exp _ {10} ^ {4}(7.18045)}$
9	387,420,489	4,28125 × 10 369 693 099	${\ Displaystyle \ exp _ {10} ^ {3}(8.56784)}$(4,1 × 10 369 693 099 cyfr)	${\ Displaystyle \ exp _ {10} ^ {4}(8.56784)}$
10	10 000 000 000	10 10 000 000 000	${\ Displaystyle \ exp _ {10} ^ {3}(10)}$(10 10 000 000 000 + 1 cyfra)	${\ Displaystyle \ exp _ {10} ^ {4}(10)}$

Nieruchomości

Tetracja ma kilka właściwości, które są podobne do potęgowania, a także właściwości, które są specyficzne dla operacji i są tracone lub uzyskiwane z potęgowania. Ponieważ potęgowanie nie dojeżdża , zasady i produktów energetycznych nie mają analog z tetracja; oświadczenia i nie są prawdziwe w większości przypadków. ${\textstyle {}^{a}\left({}^{b}x\right)=\left({}^{ab}x\right)}$${\textstyle {}^{a}\left(xy\right)={}^{a}x{}^{a}y}$

Jednak tetracja ma inną właściwość, w której . Najwyraźniej ten fakt pokazuje definicja rekurencyjna. Z tej własności wynika dowód , który pozwala na przełączanie b i c w pewnych równaniach. Dowód wygląda następująco: ${\textstyle {}^{a}x=x^{\lewo({}^{a-1}x\prawo)}}$${\ Displaystyle \ lewo ({} ^ {b} a \ po prawej) ^ {\ po lewej ({} ^ {c} a \ po prawej)} = \ po lewej ({} ^ {c + 1} a \ po prawej) ^ { \left({}^{b-1}a\right)}}$

${\ Displaystyle {\ zacząć {wyrównany} i \ lewo ({} ^ {b} a \ po prawej) ^ {\ po lewej ({} ^ {c} a \ po prawej)} \ \ = {} i \ po lewej (a ^ {{}^{b-1}a}\prawo)^{\lewo({}^{c}a\prawo)}\\={}&a^{\lewo({}^{b-1}a \right)\left({}^{c}a\right)}\\={}&a^{\left({}^{c}a\right)\left({}^{b-1}a \right)}\\={}&\left({}^{c+1}a\right)^{\left({}^{b-1}a\right)}\end{aligned}}}$

Gdy liczby x i 10 są względnie pierwsze , możliwe jest obliczenie ostatnich m cyfr dziesiętnych przy użyciu twierdzenia Eulera , dla dowolnej liczby całkowitej m . ${\ Displaystyle \ \! \ ^ {a} x}$

Kierunek oceny

Podczas oceny tetracji wyrażonej jako „wieża potęgowania”, potęgowanie seryjne jest wykonywane najpierw na najgłębszym poziomie (w notacji, na wierzchołku). Na przykład:

${\ Displaystyle \ \! \ ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 2 ^ {\ po lewej (2 ^ {\ po lewej (2 ^ {2} \ po prawej)} \ po prawej)}=2^{\lewo(2^{4}\prawo)}=2^{16}=65,\!536}$

Ta kolejność jest ważna, ponieważ potęgowanie nie jest asocjacyjne , a ocena wyrażenia w odwrotnej kolejności doprowadzi do innej odpowiedzi:

${\ Displaystyle \ \! 2 ^ {2 ^ {2 ^ {2}}} \ neq \ lewo ({\ lewo (2 ^ {2} \ po prawej)} ^ {2} \ po prawej) ^ {2} = 4^{2\cdot 2}=256}$

Ocena wyrażenia od lewej do prawej jest uważana za mniej interesującą; oceniając od lewej do prawej, każde wyrażenie można uprościć do . Z tego powodu wieże należy oceniać od prawej do lewej (lub od góry do dołu). Programiści komputerowi określają ten wybór jako prawostronnie skojarzone . ${\ Displaystyle ^ {n} a \!}$${\ Displaystyle a ^ {\ po lewej (a ^ {n-1} \ po prawej)} \! \!}$

Rozszerzenia

Tetrację można rozszerzyć na dwa różne sposoby; w równaniu zarówno podstawę a, jak i wysokość n można uogólnić przy użyciu definicji i właściwości tetracji. Chociaż podstawa i wysokość mogą być rozszerzone poza nieujemne liczby całkowite do różnych dziedzin , w tym , złożonych funkcji, takich jak , i wysokości nieskończonego n , bardziej ograniczone właściwości tetracji zmniejszają możliwość rozszerzenia tetracji. ${\ Displaystyle ^ {n} a \!}$${\ Displaystyle {^ {n} 0}}$${\ Displaystyle {} ^ {n} i}$

Rozszerzenie domeny dla baz

Baza zero

Wykładnicza nie jest spójnie zdefiniowana. Tak więc tetracje nie są jasno określone przez podany wcześniej wzór. Jest jednak dobrze zdefiniowany i istnieje: ${\displaystyle 0^{0}}$${\ Displaystyle \, {^ {n} 0}}$${\ Displaystyle \ lim _ {x \ rightarrow 0} ^ {n} x}$

${\ Displaystyle \ lim _ {x \ rightarrow 0} {} ^ {n} x = {\ zacząć {przypadki} 1, & n {\ tekst {parzyste}} \ \ 0 i n {\ tekst { nieparzyste}} \ koniec {sprawy}}}$

W ten sposób mogliśmy konsekwentnie definiować . Jest to analogiczne do definiowania . ${\ Displaystyle {} ^ {n} 0 = \ lim _ {x \ rightarrow 0} {} ^ {n} x}$${\ Displaystyle 0 ^ {0} = 1}$

Pod tym rozszerzeniem, , więc reguła z pierwotnej definicji nadal obowiązuje. ${\ Displaystyle {} ^ {0} 0 = 1}$${\ Displaystyle {^ {0}a} = 1}$

Kompleksowe bazy

Ponieważ liczby zespolone można podnosić do potęg, tetracja może być zastosowana do podstaw postaci z = a + bi (gdzie a i b są rzeczywiste). Na przykład, w ⁿ Z z z = I , tetracja uzyskuje się za pomocą głównej gałęzi logarytmu naturalnego; korzystając ze wzoru Eulera otrzymujemy zależność:

${\ Displaystyle ja ^ {a + bi} = e ^ {{\ Frac {1} {2}} {\ pi i} (a + bi)} = e ^ {- {\ Frac {1} {2}} {\pi b}}\lewo(\cos {\frac {\pi a}{2}}+i\sin {\frac {\pi a}{2}}\prawo)}$

Sugeruje to rekurencyjną definicję dla ^{n +1} i = a′ + b′i przy dowolnym ⁿ i = a + bi :

${\ Displaystyle {\ zacząć {wyrównany} a'& = e ^ {-{\ Frac {1} {2}} {\ pi b}} \ cos {\ Frac {\ pi a} {2}} \ \ [ 2pt]b'&=e^{-{\frac {1}{2}}{\pi b}}\sin {\frac {\pi a}{2}}\end{wyrównany}}}$

Można wyprowadzić następujące przybliżone wartości:

Wartości tetracji złożonych zasad

${\textstyle {}^{n}i}$	Przybliżona wartość
${\textstyle {}^{1}i=i}$	i
${\textstyle {}^{2}i=i^{\left({}^{1}i\right)}}$	0,2079
${\textstyle {}^{3}i=i^{\left({}^{2}i\right)}}$	0,9472 + 0,3208 i
${\textstyle {}^{4}i=i^{\left({}^{3}i\right)}}$	0,0501 + 0,6021 i
${\textstyle {}^{5}i=i^{\left({}^{4}i\right)}}$	0,3872 + 0,0305 i
${\textstyle {}^{6}i=i^{\lewo({}^{5}i\prawo)}}$	0,7823 + 0,5446 i
${\textstyle {}^{7}i=i^{\lewo({}^{6}i\prawo)}}$	0,1426 + 0,4005 i
${\textstyle {}^{8}i=i^{\lewo({}^{7}i\prawo)}}$	0,5198 + 0,1184 i
${\textstyle {}^{9}i=i^{\lewo({}^{8}i\prawo)}}$	0,5686 + 0,6051 i

Rozwiązanie zależności odwrotnej, tak jak w poprzedniej sekcji, daje oczekiwane ⁰ i = 1 oraz ⁻¹ i = 0 , przy ujemnych wartościach n dających nieskończone wyniki na urojonej osi. Wykreślona na płaszczyźnie zespolonej cała sekwencja skręca się spiralnie do granicy 0,4383 + 0,3606 i , co można interpretować jako wartość, w której n jest nieskończone.

Takie sekwencje tetracyjne były badane od czasów Eulera, ale są słabo poznane ze względu na ich chaotyczne zachowanie. Większość opublikowanych badań historycznie skupiała się na zbieżności nieskończenie iterowanej funkcji wykładniczej. Obecne badania bardzo skorzystały na pojawieniu się potężnych komputerów z oprogramowaniem matematycznym fraktalnym i symbolicznym. Wiele z tego, co wiadomo na temat tetracji, pochodzi z ogólnej wiedzy o złożonej dynamice i szczegółowych badaniach mapy wykładniczej.

Rozszerzenia domeny na różne wysokości

Nieskończone wysokości

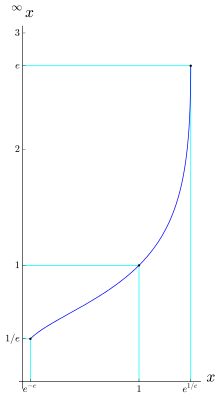
Tetracja może być rozszerzona na nieskończoną wysokość; tj. dla pewnych wartości a i n w , istnieje dobrze zdefiniowany wynik dla nieskończonego n . Dzieje się tak, ponieważ dla zasad w pewnym przedziale tetracja zbiega się do skończonej wartości, ponieważ wysokość dąży do nieskończoności . Na przykład zbiega się do 2, a zatem można powiedzieć, że jest równy 2. Tendencję w kierunku 2 można zobaczyć, oceniając małą skończoną wieżę: ${\ Displaystyle {} ^ {n} a}$${\ Displaystyle {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}}}}$

${\ Displaystyle {\ zacząć {wyrównany} {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2 }}^{1.414}}}}}&\ok {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.63 }}}}\\&\ok {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.76}}}\\&\ok {\sqrt {2 }}^{{\sqrt {2}}^{1.84}}\\&\ok {\sqrt {2}}^{1.89}\\&\ok 1,93\end{wyrównany}}}$

Ogólnie rzecz biorąc, nieskończenie iterowany wykładniczy , zdefiniowany jako granica, gdy n zmierza do nieskończoności, jest zbieżny dla e ^{− e} ≤ x ≤ e ^{1/ e} , w przybliżeniu w przedziale od 0,066 do 1,44, co pokazał Leonhard Euler . Granica, jeśli istnieje, jest dodatnim rzeczywistym rozwiązaniem równania y = x ^y . Zatem x = y ^{1/ y} . Granica określająca nieskończoną wykładniczą wartość x nie istnieje, gdy x > e ^{1/ e,} ponieważ maksimum y ^{1/ y} wynosi e ^{1/ e} . Granica również nie istnieje, gdy 0 < x < e ^{− e} . ${\ Displaystyle x ^ {x ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}} \! \!}$${\ Displaystyle {} ^ {n} x}$

Można to rozszerzyć do liczb zespolonych z z definicją:

${\ Displaystyle {} ^ {\ infty} z = z ^ {z ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}} = {\ Frac {\ operatorname {W} (- \ ln {z}) }{-\ln {z}}}~,}$

gdzie W reprezentuje funkcję W Lamberta .

Ponieważ granica y = ^∞ x (jeśli istnieje na dodatniej prostej rzeczywistej, tj. dla e ^{− e} ≤ x ≤ e ^{1/ e} ) musi spełniać x ^y = y , widzimy, że x ↦ y = ^∞ x to (niższa gałąź ) odwrotna funkcja y ↦ x = y ^{1/ y} .

Ujemne wysokości

Możemy użyć rekurencyjnej reguły dla tetracji,

${\ Displaystyle {^ {k + 1} a} = a ^ {\ lewo ({^ {k} a} \ prawej)}}$

udowodnić : ${\ Displaystyle {} ^ {-1} a}$

${\ Displaystyle ^ {k} a = \ log _ {a} \ lewo (^ {k + 1} a \ po prawej);}$

Podstawiając -1 za k daje

${\ Displaystyle {} ^ {-1} a = \ log _ {a} \ lewo ({} ^ {0} a \ prawej) = \ log _ {a} 1 = 0}$.

Mniejsze wartości ujemne nie mogą być w ten sposób dobrze zdefiniowane. Podstawiając -2 do k w tym samym równaniu daje

${\ Displaystyle {} ^ {-2} a = \ log _ {a} \ lewo ({} ^ {-1} a \ po prawej) = \ log _ {a} 0 = - \ infty}$

co nie jest dobrze zdefiniowane. Czasami jednak można je uznać za zestawy.

Dla , każda definicja jest zgodna z regułą, ponieważ ${\displaystyle n=1}$${\ Displaystyle \ \! {^ {-1} 1}}$

${\ Displaystyle {^ {0}1} = 1 = 1 ^ {n}}$dla każdego .${\ Displaystyle \ \! n = {^ {-1} 1}}$

Prawdziwe wysokości

W chwili obecnej nie ma powszechnie akceptowanego rozwiązania ogólnego problemu rozszerzania tetracji na rzeczywiste lub zespolone wartości n . Istnieje jednak wiele podejść do tego problemu, a różne podejścia przedstawiono poniżej.

Ogólnie rzecz biorąc, problem polega na znalezieniu — dla każdej rzeczywistej a > 0 — funkcji superwykładniczej nad rzeczywistym x > -2, która spełnia ${\ Displaystyle \, f (x) = {} ^ {x} a}$

• ${\ Displaystyle \ {} ^ {-1} a = 0}$
• ${\ Displaystyle \ {} ^ {0}a = 1}$
• ${\ Displaystyle \ {} ^ {x} a = a ^ {\ lewo ({} ^ {x-1} a \ prawej)}}$dla wszystkich prawdziwych ${\displaystyle x>-1.}$

Aby znaleźć bardziej naturalne rozszerzenie, zwykle wymagane jest jedno lub więcej dodatkowych wymagań. Jest to zwykle zbiór następujących elementów:

• Ciągłość wymaganie (zwykle tak, że w sposób ciągły zarówno w zmiennych dla ).${\ Displaystyle {} ^ {x} a}$${\displaystyle x>0}$
• Różniczkowalność wymaganie (może być jeden, dwa, k razy lub nieskończenie różniczkowalną w X ).
• Regularność wymaganie (co oznacza dwukrotnie różniczkowalną w X ), które:

${\ Displaystyle \ lewo ({\ Frac {d ^ {2}} {dx ^ {2}}} f (x) > 0 \ prawej)}$ dla wszystkich ${\displaystyle x>0}$

Czwarty wymóg różni się w zależności od autora i podejścia. Istnieją dwa główne podejścia do rozszerzenia tetracji do rzeczywistych wysokości; jeden opiera się na wymogu regularności , a drugi na wymogu różnicowalności . Te dwa podejścia wydają się tak różne, że mogą nie zostać pogodzone, ponieważ dają wyniki niezgodne ze sobą.

Gdy jest zdefiniowany dla przedziału o długości jeden, cała funkcja łatwo następuje dla wszystkich x > −2 . ${\ Displaystyle \ {} ^ {x} a}$

Przybliżenie liniowe dla rzeczywistych wysokości

Przybliżenie liniowa (roztwór do wymogu ciągłości, zbliżenie się do wymogu różniczkowalność) jest dane przez:

${\ Displaystyle {} ^ {x} a \ około {\ zacząć {przypadki} \ log _ {a} \ lewo (^ {x + 1} a \ po prawej) & x \ leq -1 \ \ 1 + x i -1 < x\leq 0\\a^{\left(^{x-1}a\right)}&0<x\end{przypadki}}}$

W związku z tym:

Liniowe wartości przybliżenia

Przybliżenie	Domena
${\textstyle {}^{x}a\ok x+1}$	dla -1 < x < 0
${\textstyle {}^{x}a\ok a^{x}}$	dla 0 < x < 1
${\textstyle {}^{x}a\ok a^{a^{(x-1)}}}$	dla 1 < x < 2

i tak dalej. Jest jednak różniczkowalny tylko odcinkowo; przy wartościach całkowitych x pochodna jest mnożona przez . Jest ciągle różniczkowalny dla wtedy i tylko wtedy, gdy . Na przykład, korzystając z tych metod i${\ Displaystyle \ ln {a}}$${\displaystyle x>-2}$${\displaystyle a=e}$${\ Displaystyle {} ^ {\ Frac {\ pi} {2}} e \ około 5,868...}$${\ Displaystyle {} ^ {-4,3} 0,5 \ około 4.03335 ...}$

Główne twierdzenie w artykule Hooshmanda brzmi: Niech . Jeżeli jest ciągły i spełnia warunki: ${\displaystyle 0<a\neq 1}$${\displaystyle f:(-2+\infty)\rightarrow \mathbb {R}}$

• ${\ Displaystyle f (x) = a ^ {f (x-1)} \; \; {\ tekst {dla wszystkich}} \; \; x>-1, \; f (0) = 1,}$
• ${\displaystyle f}$jest różniczkowalna na (−1, 0) ,
• ${\displaystyle f^{\prim}}$jest funkcją nie malejącą lub nierosnącą na (−1, 0) ,
• ${\ Displaystyle f ^ {\ prime} \ lewo (0 ^ {+} \ prawej) = (\ ln a) f ^ {\ prime} \ lewo (0 ^ {-} \ prawej) {\ tekst {lub}} f^{\prime }\left(-1^{+}\right)=f^{\prime }\left(0^{-}\right).}$

to jest jednoznacznie określone przez równanie ${\displaystyle f}$

${\ Displaystyle f (x) = \ exp _ {a} ^ {[x]} \ lewo (a ^ {(x)} \ prawej) = \ exp _ {a} ^ {[x + 1]} ((( x))\quad {\text{dla wszystkich}}\;\;x>-2,}$

gdzie oznacza ułamkowej części x i jest - iteracyjnego działanie funkcji . ${\ Displaystyle (x) = x-[x]}$${\ Displaystyle \ exp _ {a} ^ {[x]}}$${\displaystyle [x]}$${\displaystyle \exp _{a}}$

Dowodem jest to, że warunki od drugiego do czwartego w trywialny sposób implikują, że f jest funkcją liniową na [−1, 0] .

Liniowe przybliżenie do naturalnej funkcji tetracyjnej jest ciągle różniczkowalne, ale jego druga pochodna nie istnieje w wartościach całkowitych jej argumentu. Hooshmand wyprowadził dla niego inne twierdzenie o jednoznaczności, które stwierdza: ${\ Displaystyle {} ^ {x} e}$

Jeśli jest funkcją ciągłą, która spełnia: ${\displaystyle f:(-2+\infty)\rightarrow \mathbb {R}}$

• ${\ Displaystyle f (x) = e ^ {f (x-1)} \; \; {\ tekst {dla wszystkich}} \; \; x>-1, \; f (0) = 1,}$
• ${\displaystyle f}$jest wypukła na (−1, 0) ,
• ${\ Displaystyle f ^ {\ prime} \ lewo (0 ^ {-} \ prawej) \ leq f ^ {\ prime} \ lewo (0 ^ {+} \ po prawej).}$

następnie . [Oto imię Hooshmanda dla liniowego przybliżenia do naturalnej funkcji tetracyjnej.] ${\ Displaystyle f = {\ tekst {uxp}}}$${\ Displaystyle f = {\ tekst {uxp}}}$

Dowód jest taki sam jak poprzednio; równanie rekurencji zapewnia, że a następnie warunek wypukłości implikuje, że jest liniowy na (−1, 0) . ${\ Displaystyle f ^ {\ prime} (-1 ^ {+}) = f ^ {\ prime} (0 ^ {+}),}$${\displaystyle f}$

W związku z tym aproksymacji liniowej naturalnego tetracja jest jedynym rozwiązaniem równania i który jest wypukły w (-1 + ∞) . Wszystkie inne wystarczająco różniczkowe rozwiązania muszą mieć punkt przegięcia na przedziale (-1, 0) . ${\ Displaystyle f (x) = e ^ {f (x-1)} \; \; (x>-1)}$${\ Displaystyle f (0) = 1}$

Przybliżenia wyższego rzędu dla rzeczywistych wysokości

Poza przybliżeniami liniowymi przybliżenie kwadratowe (do wymagania różniczkowalności) jest podane przez:

${\ Displaystyle {} ^ {x} a \ około {\ zacząć {przypadki} \ log _ {a} \ lewo ({} ^ {x + 1} a \ po prawej) & x \ leq -1 \ \ 1 + {\ frac {2\ln(a)}{1\;+\;\ln(a)}}x-{\frac {1\;-\;\ln(a)}{1\;+\;\ln (a)}}x^{2}&-1<x\leq 0\\a^{\left({}^{x-1}a\right)}&x>0\end{przypadki}}}$

który jest różniczkowalny dla wszystkich , ale nie podwójnie różniczkowalny. Na przykład, jeśli jest to to samo, co przybliżenie liniowe. ${\displaystyle x>0}$${\ Displaystyle {} ^ {\ Frac {1} {2}} 2 \ około 1.45933 ...}$${\displaystyle a=e}$

Ze względu na sposób jej obliczania funkcja ta nie "anuluje", w przeciwieństwie do wykładników, gdzie . Mianowicie, ${\ Displaystyle \ lewo (a ^ {\ Frac {1} {n}} \ po prawej) ^ {n} = a}$

${\ Displaystyle {} ^ {n} \ lewo ({} ^ {\ Frac {1} {n}} a \ po prawej) = \ underbrace {\ lewo ({} ^ {\ Frac {1} {n}} a \right)^{\left({}^{\frac {1}{n}}a\right)^{\cdot ^{\cdot ^{\cdot ^{\cdot ^{\left({}^{ \frac {1}{n}}a\right)}}}}}}} _{n}\neq a}$.

Tak jak istnieje przybliżenie kwadratowe, istnieją również przybliżenia sześcienne i metody uogólniania do przybliżeń stopnia n , chociaż są one znacznie bardziej nieporęczne.

Złożone wysokości

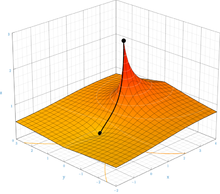
Udowodniono, że istnieje unikalna funkcja F, która jest rozwiązaniem równania F ( z + 1) = exp( F ( z )) i spełnia dodatkowe warunki, że F (0) = 1 i F ( z ) zbliża się do stałych punktów logarytmu (w przybliżeniu 0,318 ± 1,337 i ), gdy z zbliża się do ± i ∞ i że F jest holomorficzny w całej złożonej płaszczyźnie z , z wyjątkiem części osi rzeczywistej w z ≤ -2 . Dowód ten potwierdza poprzednie przypuszczenie . Konstrukcja takiej funkcji została pierwotnie zademonstrowana przez Knesera w 1950 roku. Złożoną mapę tej funkcji pokazano na rysunku po prawej stronie. Dowód działa również dla innych zasad oprócz e , o ile podstawa jest większa niż . Kolejne prace rozszerzyły konstrukcję na wszystkie złożone bazy. Złożona aproksymacja podwójnej precyzji tej funkcji jest dostępna online. ${\ Displaystyle e ^ {\ Frac {1} {e}} \ około 1,445}$

Wymóg, aby tetracja była holomorficzna, jest ważny dla jej unikalności. Wiele funkcji S można skonstruować jako

${\ Displaystyle S (z) = F \! \ lewo (~ z ~ + \ suma _ {n = 1} ^ {\ infty} \ grzech (2 \ pi nz) ~ \ alfa _ {n} + \ suma _ {n=1}^{\infty }{\duża (}1-\cos(2\pi nz){\duża )}~\beta _{n}\prawo)}$

gdzie α i β są ciągami rzeczywistymi , które zanikają wystarczająco szybko , aby zapewnić zbieżność szeregu , przynajmniej przy umiarkowanych wartościach Im  z .

Funkcja S spełnia równania tetracyjne S ( z + 1) = exp( S ( z )) , S (0) = 1 , a jeśli α _n i β _n zbliżają się do 0 wystarczająco szybko, będzie analityczne na sąsiedztwie dodatnich oś rzeczywista. Jednakże, jeśli pewne elementy { alfa } lub { p } nie zero, wówczas funkcjonować S ma lud dodatkowych osobliwości oraz cutlines w złożonej płaszczyźnie, ze względu na gwałtowny wzrost sin a cos wzdłuż osi urojonej; im mniejsze współczynniki { α } i { β } , tym dalej te osobliwości są od osi rzeczywistej.

Rozszerzenie tetracji na płaszczyznę złożoną jest zatem niezbędne dla wyjątkowości; rzeczywistym analityczna tetracja nie jest wyjątkowa.

Nieelementarna rekursywność

Tetracja (ograniczona do ) nie jest elementarną funkcją rekurencyjną . Indukcją można udowodnić, że dla każdej elementarnej funkcji rekurencyjnej f istnieje stała c taka, że ${\ Displaystyle \ mathbb {N} ^ {2}}$

${\ Displaystyle f (x) \ leq \ underbrace {2 ^ {2 ^ {\ cdot ^ {\ cdot ^ {x}}}}} _ {c}.}$

Prawą stronę oznaczamy symbolem . Przypuśćmy przeciwnie, że tetracja jest elementarną rekurencyjną. jest również elementarną rekurencyjną. Przez powyższą nierówność istnieje stała c taka, że . Pozwalając , mamy to , sprzeczność. ${\displaystyle g(c,x)}$${\displaystyle g(x,x)+1}$${\ Displaystyle g (x, x) + 1 \ leq g (c, x)}$${\displaystyle x=c}$${\displaystyle g(c,c)+1\leq g(c,c)}$

Operacje odwrotne

Potęgowanie ma dwie operacje odwrotne; pierwiastki i logarytmy . Analogicznie, odwrotności tetracji są często nazywane super-korzeniem i super-logarytmem (w rzeczywistości wszystkie hiperoperacje większe lub równe 3 mają analogiczne odwrotności); na przykład, w funkcji , dwa odwrotne są bardzo root kostka Y i super podstawa logarytmu  r z X . ${\ Displaystyle {^ {3}} y = x}$

Super root

Super pierwiastek jest odwrotną operacją tetracji względem podstawy: jeśli , to y jest n- tym nadrzędnym pierwiastkiem x ( lub ). ${\ Displaystyle ^ {n} y = x}$${\ Displaystyle {\ sqrt [{n}] {x}} _ {s}}$${\ Displaystyle {\ sqrt [{n}] {x}} {4}}$

Na przykład,

${\ Displaystyle ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 65 {} 536}$

więc 2 jest czwartym nadrzędnym pierwiastkiem z 65 536.

Kwadratowy super root

2nd-order super-korzeń , plac super-korzeń , albo bardzo pierwiastek kwadratowy ma dwa równoważne notacji, i . Jest to odwrotność funkcji Lamberta W i można ją przedstawić za pomocą funkcji W Lamberta : ${\ Displaystyle \ operatorname {ssrt} (x)}$${\ Displaystyle {\ sqrt {x}} _ {s}}$${\ Displaystyle ^ {2} x = x ^ {x}}$

${\ Displaystyle \ operatorname {ssrt} (x) = e ^ {W (\ ln x)} = {\ Frac {\ ln x} {W (\ ln x)}}}$

Funkcja ilustruje również refleksyjną naturę funkcji pierwiastka i logarytmu, ponieważ poniższe równanie jest prawdziwe tylko wtedy, gdy : ${\ Displaystyle y = \ operatorname {ssrt} (x)}$

${\ Displaystyle {\ sqrt [{y}] {x}} = \ log _ {y} x}$

Podobnie jak pierwiastki kwadratowe , superpierwiastek kwadratowy x może nie mieć jednego rozwiązania. W przeciwieństwie do pierwiastków kwadratowych, określenie liczby superpierwiastków kwadratowych z x może być trudne. Ogólnie rzecz biorąc, jeśli , to x ma dwa dodatnie superpierwiastki kwadratowe między 0 a 1; i jeśli , to x ma jeden dodatni superpierwiastek kwadratowy większy niż 1. Jeśli x jest dodatnie i mniejsze niż to nie ma żadnych rzeczywistych superpierwiastków kwadratowych, ale wzór podany powyżej daje przeliczalnie nieskończenie wiele złożonych pierwiastków dla dowolnego skończonego x nie równa 1. Funkcja została wykorzystana do określenia wielkości klastrów danych . ${\ Displaystyle e ^ {-1 / e} < x < 1}$${\displaystyle x>1}$${\ Displaystyle e ^ {-1 / e}}$

O : ${\displaystyle x=1}$

${\ Displaystyle \ operatorname {ssqrt} (x) = 1 + (x-1)-(x-1) ^ {2} + {\ Frac {3} {2}} (x-1) ^ {3}- {\frac {17}{6}}(x-1)^{4}+{\frac {37}{6}}(x-1)^{5}-{\frac {1759}{120}} (x-1)^{6}+{\frac {13279}{360}}(x-1)^{7}+\mathrm {O} \left((x-1)^{8}\right) }$

Inne super-korzenie

Dla każdej liczby całkowitej n > 2 , funkcja ⁿ x jest zdefiniowana i wzrastająca dla x ≥ 1 , i ⁿ 1 = 1 , tak że n- ty nadrzędny pierwiastek x , , istnieje dla x ≥ 1 . ${\ Displaystyle {\ sqrt [{n}] {x}} _ {s}}$

Jedną z prostszych i szybszych formuł dla superkorzenia trzeciego stopnia jest formuła rekurencyjna, jeśli: "x ^ x ^ x = a", a następnie x (n + 1) = exp (W (W (x (n ) * ln (a)))), na przykład x (0) = 1.

Jednakże, jeśli stosuje się powyższe przybliżenie liniowe , to jeśli -1 < y ≤ 0 , więc nie może istnieć. ${\ Displaystyle ^ {y} x = y + 1}$${\ Displaystyle ^ {y} {\ sqrt {y + 1}} _ {s}}$

W taki sam sposób jak super-pierwiastek kwadratowy, terminologia dla innych super pierwiastków może być oparta na normalnych pierwiastkach : „super-korzenie sześcienne” można wyrazić jako ; „czwarty super-korzeń” można wyrazić jako ; a " n- tym super-korzeniem" jest . Zauważ, że może nie być jednoznacznie zdefiniowane, ponieważ może być więcej niż jeden n- ^ty korzeń. Na przykład x ma jeden (rzeczywisty) nadrzędny pierwiastek główny, jeśli n jest nieparzyste , a maksymalnie dwa, jeśli n jest parzyste . ${\ Displaystyle {\ sqrt [{3}] {x}} _ {s}}$${\ Displaystyle {\ sqrt [{4}] {x}} _ {s}}$${\ Displaystyle {\ sqrt [{n}] {x}} _ {s}}$${\ Displaystyle {\ sqrt [{n}] {x}} _ {s}}$

Podobnie jak w przypadku rozszerzenia tetracji do nieskończonych wysokości, super-korzenia można rozszerzyć do n = ∞ , będąc dobrze zdefiniowanym, jeśli 1/ e ≤ x ≤ e . Zauważ, że i tym samym . Dlatego, gdy jest dobrze zdefiniowany i, w przeciwieństwie do normalnej tetracji, jest funkcją elementarną . Na przykład . ${\ Displaystyle x = {^ {\ infty} y} = ^ {\ lewo [^ {\ infty} y \ prawo]} = y ^ {x}}$${\ Displaystyle y = x ^ {1/x}}$${\ Displaystyle {\ sqrt [{\ infty}] {x}} _ {s} = x ^ {1/x}}$${\ Displaystyle {\ sqrt [{\ infty}] {2}} _ {s} = 2 ^ {1/2} = {\ sqrt {2}}}$

Z twierdzenia Gelfonda-Schneidera wynika, że superpierwiastek dla dowolnej dodatniej liczby całkowitej n jest liczbą całkowitą lub transcendentalną i jest liczbą całkowitą lub nieracjonalną. Pytaniem otwartym pozostaje, czy irracjonalne superkorzenie są w tym drugim przypadku transcendentalne. ${\ Displaystyle {\ sqrt {n}} _ {s}}$${\ Displaystyle {\ sqrt [{3}] {n}} _ {s}}$

Superlogarytm

Po wybraniu stale rosnącej (w x ) definicji tetracji, ^x a , odpowiedni superlogarytm lub jest zdefiniowany dla wszystkich liczb rzeczywistych x i a > 1 . ${\ Displaystyle \ operatorname {slog} _ {a} x}$${\ Displaystyle \ log _ {a} ^ {4}x}$

Funkcja slog _a  x spełnia:

${\ Displaystyle {\ zacząć {tablica} {lcl} \ operatorname {slog} _ {a} {^ {x} i = & x \ \ \ operatorname {slog} _ {a} a ^ {x} i = i 1+ \operator {slog} _{a}x\\\operator {slog} _{a}x&=&1+\operator {slog} _{a}\log _{a}x\\\operator {slog} _{a }x&>&-2\end{tablica}}}$

Otwarte pytania

Poza problemami z rozszerzeniami tetratacji, istnieje kilka otwartych pytań dotyczących tetracji, szczególnie w odniesieniu do relacji między systemami liczbowymi, takimi jak liczby całkowite i niewymierne :

• Nie wiadomo, czy występuje dodatnia n w którym ⁿ Õ lub ⁿ e jest liczbą całkowitą. W szczególności nie wiadomo, czy liczba ⁴ π czy ⁵ e jest liczbą całkowitą.
• Nie wiadomo, czy ⁿ q jest liczbą całkowitą dla dowolnej dodatniej liczby całkowitej n i dodatniej niecałkowitej liczby wymiernej q . Na przykład nie wiadomo, czy pierwiastek dodatni równania ⁴ x = 2 jest liczbą wymierną.

Zobacz też

• Funkcja Ackermanna
• notacja duże O
• Podwójna funkcja wykładnicza
• Hiperoperacja
• Iterowany logarytm
• Arytmetyka wskaźnika poziomu symetrycznego

Uwagi

Bibliografia

• Daniel Geisler, Tetracja
• Ioannis Galidakis, O rozszerzeniu hiper4 na liczby niecałkowite (bez daty, 2006 lub wcześniej) (Prostszy, łatwiejszy do odczytania przegląd następnego źródła )
• Ioannis Galidakis, On Extending hyper4 i Knuth's Up-arrow Notation to the Reals (bez daty, 2006 lub wcześniej).
• Robert Munafo, Rozszerzenie funkcji hyper4 na liczby rzeczywiste (Nieformalna dyskusja na temat rozszerzenia tetracji na liczby rzeczywiste).
• Lode Vandevenne, Tetracja pierwiastka kwadratowego z dwójki . (2004). (Próba rozszerzenia tetracji na liczby rzeczywiste.)
• Ioannis Galidakis, Matematyka , (Ostateczna lista odniesień do badań nad tetracją. Wiele informacji na temat funkcji Lamberta W, powierzchni Riemanna i kontynuacji analitycznej.)
• Joseph MacDonell, Niektóre krytyczne punkty funkcji hipermocy .
• Dave L. Renfro, Strony internetowe dla nieskończenie iterowanych wykładników
• Knobel, R. (1981). „Wykładnicze powtórzone”. Amerykański miesięcznik matematyczny . 88 (4): 235–252. doi : 10.1080/00029890.1981.11995239 .
• Hans Maurer, „ Uber die Funktion für ganzzahliges Argument (Abundanzen).” Mittheilungen der Mathematische Gesellschaft w Hamburgu 4 (1901), s. 33-50. (Odniesienie do użycia z artykułu Knobla.)${\ Displaystyle y = x ^ {[x ^ {[x (\ cdots)]}]}}$ ${\ Displaystyle \ {^ {n} a}}$
• Czwarta operacja
• Luca Moroni, Dziwne właściwości nieskończonej wieży mocy ( https://arxiv.org/abs/1908.05559 )

Dalsza lektura

• Galidakis, Ioannis; Weisstein, Eric Wolfgang . "Wieża Mocy" . MatematykaŚwiat . Źródło 2019-07-05 .