Wariacyjne metody bayesowskie - Variational Bayesian methods

Wariacyjne metody bayesowskie to rodzina technik aproksymacji nierozwiązalnych całek powstających we wnioskowaniu bayesowskim i uczeniu maszynowym . Są one zwykle używane w złożonych modelach statystycznych składających się z obserwowanych zmiennych (zwykle określanych jako „dane”), a także nieznanych parametrów i zmiennych ukrytych , z różnymi rodzajami relacji między trzema typami zmiennych losowych , które można opisać za pomocą modelu graficznego . Jak to jest typowe we wnioskowaniu bayesowskim, parametry i zmienne latentne są grupowane razem jako „zmienne nieobserwowane”. Wariacyjne metody bayesowskie są używane głównie do dwóch celów:

1. Aby zapewnić analityczne przybliżenie prawdopodobieństwa a posteriori nieobserwowanych zmiennych, w celu wnioskowania statystycznego na temat tych zmiennych.
2. Aby wyprowadzić dolną granicę dla marginalnego prawdopodobieństwa (czasami nazywanego „dowodem”) obserwowanych danych (tj. marginalnego prawdopodobieństwa danych danego modelu, z marginalizacją wykonywaną na nieobserwowanych zmiennych). Jest to zwykle używane do przeprowadzania wyboru modelu , przy czym ogólna idea polega na tym, że wyższe marginalne prawdopodobieństwo dla danego modelu wskazuje na lepsze dopasowanie danych przez ten model, a zatem większe prawdopodobieństwo, że dany model był tym, który wygenerował dane. (Zobacz także artykuł o współczynniku Bayesa ).

W pierwszym celu (aproksymacji prawdopodobieństwa a posteriori) wariacyjne metody Bayesa są alternatywą dla metod Monte Carlo — w szczególności metod Monte Carlo z łańcuchem Markowa , takich jak próbkowanie Gibbsa — dla przyjęcia w pełni bayesowskiego podejścia do wnioskowania statystycznego w przypadku złożonych rozkładów, które są trudne do bezpośredniej oceny lub próby . W szczególności, podczas gdy techniki Monte Carlo zapewniają aproksymację numeryczną dokładnego odcinka tylnego przy użyciu zestawu próbek, Bayes wariacyjny zapewnia lokalnie optymalne, dokładne rozwiązanie analityczne do przybliżenia odcinka tylnego.

Wariacyjne Bayesa można postrzegać jako rozszerzenie algorytmu EM ( maksymalizacja oczekiwań ) od maksymalnej estymacji a posteriori ( estymacja MAP) pojedynczej najbardziej prawdopodobnej wartości każdego parametru do pełnej estymacji bayesowskiej, która oblicza (przybliżenie) cały rozkład a posteriori parametrów i zmiennych ukrytych. Podobnie jak w EM, znajduje zestaw optymalnych wartości parametrów i ma taką samą naprzemienną strukturę jak EM, opartą na zestawie wzajemnie powiązanych (wzajemnie zależnych) równań, których nie można rozwiązać analitycznie.

W wielu zastosowaniach wariacyjne Bayes tworzy rozwiązania o dokładności porównywalnej do próbkowania Gibbsa z większą szybkością. Jednak wyprowadzenie zestawu równań używanego do iteracyjnego aktualizowania parametrów często wymaga dużej ilości pracy w porównaniu z wyprowadzeniem porównywalnych równań próbkowania Gibbsa. Dzieje się tak nawet w przypadku wielu modeli, które są koncepcyjnie dość proste, jak pokazano poniżej w przypadku podstawowego modelu niehierarchicznego z tylko dwoma parametrami i bez zmiennych ukrytych.

Wyprowadzenie matematyczne

Problem

We wnioskowaniu wariacyjnym rozkład a posteriori nad zbiorem zmiennych nieobserwowanych przy pewnych danych jest aproksymowany przez tzw. rozkład wariacyjny , : ${\ Displaystyle \ mathbf {Z} = \ {Z_ {1} \ kropki Z_ {n} \}}$${\ Displaystyle \ mathbf {X}}$${\ Displaystyle Q (\ mathbf {Z} )}$

${\ Displaystyle P (\ mathbf {Z} \ mid \ mathbf {X}) \ w przybliżeniu Q (\ mathbf {Z}).}$

Rozkład jest ograniczony do rodziny rozkładów o prostszej formie (np. rodzina rozkładów Gaussa) niż , wybranych z zamiarem upodobnienia do prawdziwego a posteriori, . ${\ Displaystyle Q (\ mathbf {Z} )}$${\ Displaystyle P (\ mathbf {Z} \ mid \ mathbf {X})}$${\ Displaystyle Q (\ mathbf {Z} )}$${\ Displaystyle P (\ mathbf {Z} \ mid \ mathbf {X})}$

Podobieństwo (lub odmienność) mierzy się w kategoriach funkcji odmienności, a zatem wnioskowanie odbywa się poprzez wybór rozkładu, który minimalizuje . ${\ Displaystyle d (Q; P)}$${\ Displaystyle Q (\ mathbf {Z} )}$${\ Displaystyle d (Q; P)}$

Rozbieżność KL

Najpopularniejszy typ wariacji Bayes wykorzystuje rozbieżność Kullbacka-Leiblera ( rozbieżność KL) P z Q jako wybór funkcji niepodobieństwa. Ten wybór sprawia, że ​​ta minimalizacja jest wykonalna. Rozbieżność KL jest zdefiniowana jako

${\ Displaystyle D_ {\ operatorname {KL} } (Q \ P równoległy) \ trójkąt \ suma _ {\ mathbf {Z}} Q (\ mathbf {Z} ) \ log {\ Frac {Q (\ mathbf {Z} )}{P(\mathbf {Z} \mid \mathbf {X} )}}.}$

Zauważ, że Q i P są odwrotne od tego, czego można by się spodziewać. To użycie odwróconej dywergencji KL jest koncepcyjnie podobne do algorytmu maksymalizacji oczekiwań . (Użycie dywergencji KL w inny sposób daje algorytm propagacji oczekiwania .)

Krnąbrność

Techniki wariacyjne są zwykle używane do tworzenia przybliżenia dla:

${\ Displaystyle P (\ mathbf {Z} \ mid \ mathbf {X} ) = {\ Frac {P (\ mathbf {X} \ mid \ mathbf {Z}) P (\ mathbf {Z})} {P ( \mathbf {X} )}}={\frac {P(\mathbf {X} \mid \mathbf {Z} )P(\mathbf {Z} )}{\int _{\mathbf {Z} }P( \mathbf {X} ,\mathbf {Z} ')\,d\mathbf {Z} '}}}$

Marginalizacja przed obliczeniem w mianowniku jest zazwyczaj niewykonalna, ponieważ np. przestrzeń poszukiwań jest kombinatorycznie duża. Dlatego szukamy przybliżenia, używając . ${\ Displaystyle \ mathbf {Z}}$${\ Displaystyle P (\ mathbf {X} )}$${\ Displaystyle \ mathbf {Z}}$${\ Displaystyle Q (\ mathbf {Z} ) \ około P (\ mathbf {Z} \ mid \ mathbf {X})}$

Dolna granica dowodów

Biorąc pod uwagę, że , powyższa rozbieżność KL może być również zapisana jako ${\ Displaystyle P (\ mathbf {Z} \ mid \ mathbf {X} ) = {\ Frac {P (\ mathbf {X}, \ mathbf {Z}}} {P (\ mathbf {X})}}}$

${\ Displaystyle D_ {\ operatorname {KL} } (Q \ równoległe P) = \ suma _ {\ mathbf {Z}} Q (\ mathbf {Z}) \ lewo [\ log {\ Frac {Q (\ mathbf { Z} )}{P(\mathbf {Z} ,\mathbf {X} )}}+\log P(\mathbf {X} )\right]=\sum _{\mathbf {Z} }Q(\mathbf {Z} )\left[\log Q(\mathbf {Z} )-\log P(\mathbf {Z} ,\mathbf {X} )\right]+\sum _{\mathbf {Z} }Q( \mathbf {Z} )\left[\log P(\mathbf {X} )\right]}$

Ponieważ jest stałą w odniesieniu do i ponieważ jest rozkładem, mamy ${\ Displaystyle P (\ mathbf {X} )}$${\ Displaystyle \ mathbf {Z}}$${\ Displaystyle \ suma _ {\ mathbf {Z}} Q (\ mathbf {Z}) = 1}$${\ Displaystyle Q (\ mathbf {Z} )}$

${\ Displaystyle D_ {\ operatorname {KL}} (Q \ parallel P) = \ suma _ {\ mathbf {Z}} Q (\ mathbf {Z}) \ lewo [\ log Q (\ mathbf {Z}) - \log P(\mathbf {Z} ,\mathbf {X} )\right]+\log P(\mathbf {X} )}$

które zgodnie z definicją wartości oczekiwanej (dla dyskretnej zmiennej losowej ) można zapisać w następujący sposób:

${\ Displaystyle D_ {\ operatorname {KL}} (Q \ równoległe P) = \ mathbb {E} _ {\ mathbf {Q}} \ lewo [\ log Q (\ mathbf {Z}) - \ log P (\ mathbf {Z} ,\mathbf {X} )\right]+\log P(\mathbf {X} )}$

które można zmienić, aby stać się

${\ Displaystyle \ log P (\ mathbf {X} ) = D_ {\ operatorname {KL}} (Q \ p równoległy) - \ mathbb {E} _ {\ mathbf {Q}} \ lewo [\ log Q (\ mathbf {Z} )-\log P(\mathbf {Z} ,\mathbf {X} )\right]=D_{\mathrm {KL} }(Q\parallel P)+{\mathcal {L}}(Q )}$

Ponieważ dowód logarytmiczny jest ustalony w odniesieniu do , maksymalizacja końcowego terminu minimalizuje rozbieżność KL od . Dzięki odpowiedniemu doborowi , staje się podatny na obliczenia i maksymalizację. Stąd mamy zarówno przybliżenie analityczne dla a posteriori , jak i dolną granicę dla dowodów (ponieważ rozbieżność KL jest nieujemna). ${\ Displaystyle \ log P (\ mathbf {X})}$${\displaystyle Q}$${\ Displaystyle {\ Mathcal {L}} (Q)}$${\displaystyle Q}$${\displaystyle P}$${\displaystyle Q}$${\ Displaystyle {\ Mathcal {L}} (Q)}$${\displaystyle Q}$${\ Displaystyle P (\ mathbf {Z} \ mid \ mathbf {X})}$${\ Displaystyle {\ Mathcal {L}} (Q)}$${\ Displaystyle \ log P (\ mathbf {X})}$

Dolna granica jest znany jako (ujemny) wariacyjną energii swobodnej analogicznie energia swobodna , ponieważ może on być wyrażony jako negatywnej energii plus entropii z . Termin ten jest również znany jako Evidence Lower Bound , w skrócie ELBO , aby podkreślić, że jest to dolna granica dowodów danych. ${\ Displaystyle {\ Mathcal {L}} (Q)}$${\ Displaystyle \ operatorname {E} _ {Q} [\ log P (\ mathbf {Z}, \ mathbf {X})]}$${\displaystyle Q}$${\ Displaystyle {\ Mathcal {L}} (Q)}$

Dowody

Za pomocą uogólnionego twierdzenia Pitagorasa o dywergencji Bregmana , którego rozbieżność KL jest szczególnym przypadkiem, można wykazać, że:

Uogólnione twierdzenie Pitagorasa dla rozbieżności Bregmana .

${\ Displaystyle D_ {\ operatorname {KL}} (Q \ operator równoległy P) \ geq D_ {\ operatorname {KL}} (Q \ operator równoległy Q ^ {*}) + D_ {\ operatorname {KL}} (Q ^ { *}\parallel P),\forall Q^{*}\in {\mathcal {C}}}$

gdzie jest zbiorem wypukłym, a równość zachodzi, jeśli: ${\displaystyle {\mathcal {C}}}$

${\ Displaystyle Q = Q ^ {*} \ triangleq \ arg \ min _ {Q \ w {\ mathcal {C}}} D_ {\ operatorname {KL}} (Q \ równoległy P).}$

W takim przypadku globalny minimalizator z można znaleźć w następujący sposób: ${\ Displaystyle Q ^ {*} (\ mathbf {Z} ) = q ^ {*} (\ mathbf {Z} _ {1} \ mid \ mathbf {Z} _ {2}) q ^ {*} (\ mathbf {Z} _{2})=q^{*}(\mathbf {Z} _{2}\mid \mathbf {Z} _{1})q^{*}(\mathbf {Z} _{ 1}),}$${\ Displaystyle \ mathbf {Z} = \ {\ mathbf {Z_ {1}} \ mathbf {Z_ {2}} \}}$

${\ Displaystyle q ^ {*} (\ mathbf {Z} _ {2}) = {\ Frac {P (\ mathbf {X}}}} {\ Zeta (\ mathbf {X})}} {\ Frac {P (\mathbf {Z} _{2}\mid \mathbf {X} )}{\exp(D_{\mathrm {KL} }(q^{*}(\mathbf {Z} _{1}\mid \ mathbf {Z} _{2})\parallel P(\mathbf {Z} _{1}\mid \mathbf {Z} _{2},\mathbf {X} )))}}={\frac {1 }{\zeta (\mathbf {X} )}}\exp \mathbb {E} _{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})} \left(\log {\frac {P(\mathbf {Z} ,\mathbf {X} )}{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2 })}}\Prawidłowy),}$

w którym stała normalizująca to:

${\ Displaystyle \ zeta (\ mathbf {X} ) = P (\ mathbf {X} ) \ int _ {\ mathbf {Z} _ {2}} {\ Frac {P (\ mathbf {Z} _ {2}) \mid \mathbf {X} )}{\exp(D_{\mathrm {KL} }(q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})\ równolegle P(\mathbf {Z} _{1}\mid \mathbf {Z} _{2},\mathbf {X} )))}}=\int _{\mathbf {Z} _{2}}\ exp \mathbb {E} _{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})}\left(\log {\frac {P(\mathbf { Z} ,\mathbf {X} )}{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})}}\right).}$

Termin ten jest często nazywany w praktyce dolną granicą dowodów ( ELBO ), ponieważ , jak pokazano powyżej. ${\ Displaystyle \ zeta (\ mathbf {X})}$${\ Displaystyle P (\ mathbf {X} ) \ geq \ zeta (\ mathbf {X} ) = \ exp ({\ mathcal {L}} (Q ^ {*}))}$

Zamieniając role i możemy iteracyjnie obliczyć aproksymowane i prawdziwe brzegi modelu i odpowiednio. Chociaż ten schemat iteracyjny gwarantuje zbieżność monotoniczną, zbieżność jest tylko lokalnym minimalizatorem . ${\ Displaystyle \ mathbf {Z} _ {1}}$${\ Displaystyle \ mathbf {Z} _ {2}}$${\ Displaystyle q ^ {*} (\ mathbf {Z} _ {1})}$${\ Displaystyle q ^ {*} (\ mathbf {Z} _ {2})}$${\ Displaystyle P (\ mathbf {Z} _ {1} \ mid \ mathbf {X})}$${\ Displaystyle P (\ mathbf {Z} _ {2} \ mid \ mathbf {X})}$${\ Displaystyle Q ^ {*}}$${\ Displaystyle D_ {\ operatorname {KL} } (Q \ P równoległy)}$

Jeżeli ograniczona przestrzeń jest zamknięta w niezależnej przestrzeni, tj . powyższy schemat iteracyjny stanie się tak zwanym przybliżeniem pola średniego, jak pokazano poniżej. ${\displaystyle {\mathcal {C}}}$${\ Displaystyle q ^ {*} (\ mathbf {Z} _ {1} \ mid \ mathbf {Z} _ {2}) = q ^ {*} (\ mathbf {Z_ {1}}}),}$${\ Displaystyle Q ^ {*} (\ mathbf {Z} ) = q ^ {*} (\ mathbf {Z} _ {1}) q ^ {*} (\ mathbf {Z} _ {2})}$

Aproksymacja średniego pola

Zazwyczaj zakłada się, że rozkład wariacyjny rozkłada się na czynniki w pewnym podziale zmiennych latentnych, tj. w przypadku pewnego podziału zmiennych latentnych na , ${\ Displaystyle Q (\ mathbf {Z} )}$${\ Displaystyle \ mathbf {Z}}$${\ Displaystyle \ mathbf {Z} _ {1} \ kropki \ mathbf {Z} _ {M}}$

${\ Displaystyle Q (\ mathbf {Z} ) = \ prod _ {i = 1} ^ {M} q_ {i} (\ mathbf {Z} _ {i} \ mid \ mathbf {X})}$

Korzystając z rachunku wariacyjnego (stąd nazwa „wariacyjny Bayes”) można wykazać, że „najlepszy” rozkład dla każdego z czynników (pod względem rozkładu minimalizującego rozbieżność KL, jak opisano powyżej) można wyrazić jako: ${\ Displaystyle q_ {j} ^ {*}}$${\displaystyle q_{j}}$

${\ Displaystyle q_ {j} ^ {*} (\ mathbf {Z} _ {j} \ mid \ mathbf {X} ) = {\ Frac {e ^ {\ operator {E} _ {i \ neq j} [ \ln p(\mathbf {Z} ,\mathbf {X} )]}}{\int e^{\operatorname {E} _{i\neq j}[\ln p(\mathbf {Z} ,\mathbf {X} )]}\,d\mathbf {Z} _{j}}}}$

gdzie jest oczekiwaniem logarytmu łącznego prawdopodobieństwa danych i zmiennych latentnych, przejętych po wszystkich zmiennych nie w podziale: patrz wyprowadzenie rozkładu . ${\ Displaystyle \ operatorname {E} _ {i \ neq j} [\ ln p (\ mathbf {Z}, \ mathbf {X})]}$${\ Displaystyle q_ {j} ^ {*} (\ mathbf {Z} _ {j} \ mid \ mathbf {X})}$

W praktyce najczęściej pracujemy logarytmicznie, czyli:

${\ Displaystyle \ ln q_ {j} ^ {*} (\ mathbf {Z} _ {j} \ mid \ mathbf {X} ) = \ operatorname {E} _ {i \ neq j} [\ ln p (\ mathbf {Z} ,\mathbf {X} )]+{\text{stała}}}$

Stała w powyższym wyrażeniu jest powiązana ze stałą normalizującą (mianownik w powyższym wyrażeniu dla ) i jest zwykle przywracana przez kontrolę, ponieważ resztę wyrażenia można zwykle rozpoznać jako znany typ rozkładu (np. Gaussian , gamma itp.). ${\ Displaystyle q_ {j} ^ {*}}$

Na podstawie właściwości oczekiwań, ekspresja może zwykle być uproszczone do funkcji stałych hiperparametrów tych stanu rozkładu powyżej zmiennych utajonych i oczekiwań (czasem wyższych momentów takich jak wariancji ) zmiennych utajonych nie w bieżącej partycji (tj ukryte zmienne nieuwzględnione w ). Tworzy to cykliczne zależności między parametrami rozkładów względem zmiennych w jednej partycji a oczekiwaniami zmiennych w pozostałych partycjach. To naturalnie sugeruje algorytm iteracyjny , podobnie jak EM ( algorytm maksymalizacji oczekiwań ), w którym oczekiwania (i ewentualnie wyższe momenty) zmiennych latentnych są inicjowane w pewien sposób (być może losowo), a następnie parametry każdego rozkładu są obliczane z kolei przy użyciu bieżących wartości oczekiwań, po czym oczekiwanie nowo obliczonego rozkładu jest odpowiednio ustawiane zgodnie z obliczonymi parametrami. Algorytm tego rodzaju gwarantuje zbieżność . ${\ Displaystyle \ operatorname {E} _ {i \ neq j} [\ ln p (\ mathbf {Z}, \ mathbf {X})]}$${\ Displaystyle \ mathbf {Z} _ {j}}$

Innymi słowy, dla każdego z podziałów zmiennych, poprzez uproszczenie wyrażenia na rozkład nad zmiennymi tego podziału i zbadanie funkcjonalnej zależności rozkładu od rozpatrywanych zmiennych, zwykle można określić rodzinę rozkładu (co z kolei determinuje wartość stałej). Wzór na parametry rozkładu będzie wyrażony w postaci hiperparametrów poprzednich rozkładów (które są znanymi stałymi), ale także w postaci oczekiwań funkcji zmiennych w innych podziałach. Zwykle oczekiwania te można uprościć do funkcji oczekiwań samych zmiennych (tj. średnich ); czasami pojawiają się również oczekiwania dotyczące zmiennych do kwadratu (które mogą być związane z wariancją zmiennych) lub oczekiwania wyższych potęg (tj. wyższych momentów ). W większości przypadków rozkłady pozostałych zmiennych będą pochodzić ze znanych rodzin i można znaleźć wzory na odpowiednie oczekiwania. Jednak formuły te zależą od parametrów tych rozkładów, które z kolei zależą od oczekiwań dotyczących innych zmiennych. W rezultacie wzory na parametry rozkładów każdej zmiennej można wyrazić jako szereg równań z wzajemnymi, nieliniowymi zależnościami między zmiennymi. Zwykle nie ma możliwości bezpośredniego rozwiązania tego układu równań. Jednak, jak opisano powyżej, zależności sugerują prosty algorytm iteracyjny, który w większości przypadków gwarantuje zbieżność. Przykład wyjaśni ten proces.

Formuła dwoistości dla wnioskowania wariacyjnego

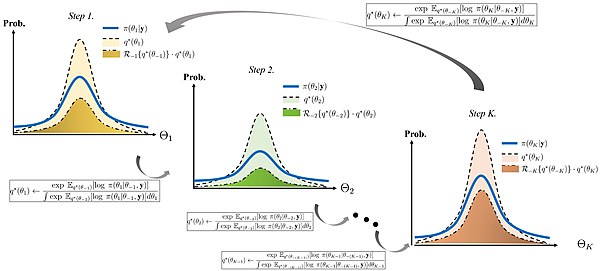
Obrazkowa ilustracja algorytmu wnioskowania wariacyjnego ze współrzędnością wznoszenia za pomocą wzoru na dualność.

Poniższe twierdzenie jest określane jako formuła dwoistości dla wnioskowania wariacyjnego. Wyjaśnia niektóre ważne właściwości rozkładów wariacyjnych stosowanych w wariacyjnych metodach Bayesa.

Twierdzenie Rozważmy dwa Przestrzeń probabilistyczna i z . Załóżmy, że istnieje wspólna dominująca miara prawdopodobieństwa, taka jak i . Pozwolić oznaczają żadnych realnych wartościach zmienną losową o który spełnia . Wtedy obowiązuje następująca równość ${\ Displaystyle (\ Theta {\ mathcal {F}}, P)}$${\ Displaystyle (\ Theta {\ mathcal {F}}, Q)}$${\ Displaystyle Q \ ll P}$ ${\ Displaystyle \ lambda}$${\ Displaystyle P \ ll \ lambda}$${\ Displaystyle Q \ ll \ lambda}$${\ Displaystyle h}$${\ Displaystyle (\ Theta {\ mathcal {F}}, P)}$${\ Displaystyle h \ w L_ {1}(P)}$

${\ Displaystyle \ log E_ {P} [\ exp h] = {\ tekst {sup}} _ {Q \ ll P} \ {E_ {Q} [h]-D_ {\ tekst {KL}} (Q \ równolegle P)\}.}$

Co więcej, supremum po prawej stronie jest osiągane wtedy i tylko wtedy, gdy się trzyma

${\displaystyle {\frac {q(\theta)}{p(\theta)}}={\frac {\exp h(\theta)}{E_{P}[\exp h]}},}$

prawie na pewno w przypadku środka prawdopodobieństwa , w którym i oznaczają pochodnych Radona-Nikodyma tych środków prawdopodobieństwa i w odniesieniu do , odpowiednio. ${\displaystyle Q}$${\displaystyle p(\theta)=DP/d\lambda}$${\displaystyle q(\theta)=dQ/d\lambda}$${\displaystyle P}$${\displaystyle Q}$${\ Displaystyle \ lambda}$

Podstawowy przykład

Rozważmy prosty niehierarchiczny model bayesowski składający się z zestawu obserwacji iid z rozkładu Gaussa , z nieznaną średnią i wariancją . Poniżej szczegółowo omówimy ten model, aby zilustrować działanie wariacyjnej metody Bayesa.

Dla matematycznej wygody w poniższym przykładzie pracujemy w kategoriach precyzji — tj. odwrotności wariancji (lub w wielowymiarowym gaussie, odwrotności macierzy kowariancji ) — a nie samej wariancji. (Z teoretycznego punktu widzenia precyzja i wariancja są równoważne, ponieważ istnieje między nimi zależność jeden do jednego ).

Model matematyczny

Umieszczamy sprzężone rozkłady wcześniejsze na nieznanej średniej i precyzji , tj. średnia również jest zgodna z rozkładem Gaussa, podczas gdy precyzja jest zgodna z rozkładem gamma . Innymi słowy: ${\ Displaystyle \ mu}$${\ Displaystyle \ tau}$

${\ Displaystyle {\ zacząć {wyrównany} \ tau i \ sim \ nazwa operatora {gamma} (a_ {0}, b_ {0}) \ \ \ mu | \ tau i \ sim {\ mathcal {N}} (\ mu _{0},(\lambda _{0}\tau )^{-1})\\\{x_{1},\dots ,x_{N}\}&\sim {\mathcal {N}}( \mu ,\tau ^{-1})\\N&={\text{liczba punktów danych}}\end{wyrównane}}}$

W hiperparametrów i w poprzednich dystrybucji są stałe, określone wartości. Można je ustawić na małe liczby dodatnie, aby uzyskać szerokie rozkłady wcześniejsze wskazujące na nieznajomość wcześniejszych rozkładów i . ${\ Displaystyle \ mu _ {0}, \ lambda _ {0}, a_ {0}}$${\displaystyle b_{0}}$${\ Displaystyle \ mu}$${\ Displaystyle \ tau}$

Otrzymujemy punkty danych, a naszym celem jest wywnioskowanie a posteriori rozkładu parametrów i${\ Displaystyle N}$${\ Displaystyle \ mathbf {X} = \ {x_ {1}, \ ldots, x_ {N} \}}$ ${\ Displaystyle q (\ mu, \ tau) = p (\ mu, \ tau \ mid x_ {1}, \ ldots, x_ {N})}$${\ Displaystyle \ mu}$${\displaystyle \tau.}$

Wspólne prawdopodobieństwo

Wspólne prawdopodobieństwo wszystkich zmiennych można zapisać jako

${\ Displaystyle p (\ mathbf {X} , \ mu , \ tau ) = p (\ mathbf {X} \ mid \ mu \ tau) p (\ mu \ mid \ tau) p (\ tau)}$

gdzie znajdują się poszczególne czynniki

${\ Displaystyle {\ zacząć {wyrównany} p (\ mathbf {X} \ mid \ mu \ tau) & = \ prod _ {n = 1} ^ {N} {\ mathcal {N}} (x_ {n} \mid \mu ,\tau ^{-1})\\p(\mu \mid \tau )&={\mathcal {N}}\left(\mu \mid \mu _{0},(\lambda _{0}\tau )^{-1}\right)\\p(\tau )&=\operatorname {Gamma} (\tau \mid a_{0},b_{0})\end{aligned}} }$

gdzie

${\ Displaystyle {\ zacząć {wyrównany} {\ mathcal {N}} (x \ mid \ mu \ sigma ^ {2}) i = {\ Frac {1} {\ sqrt {2 \ pi \ sigma ^ {2 }}}}e^{\frac {-(x-\mu )^{2}}{2\sigma ^{2}}}\\\nazwa operatora {Gamma} (\tau \mid a,b)&= {\frac {1}{\Gamma (a)}}b^{a}\tau ^{a-1}e^{-b\tau }\end{wyrównany}}}$

Przybliżenie faktoryzowane

Załóżmy, że , tj. rozkład a posteriori rozkłada się na czynniki niezależne dla i . Tego typu założenie leży u podstaw wariacyjnej metody bayesowskiej. Prawdziwy rozkład a posteriori w rzeczywistości nie uwzględnia tego w ten sposób (w rzeczywistości, w tym prostym przypadku, wiadomo, że jest to rozkład Gaussa-gamma ), a zatem otrzymany wynik będzie przybliżeniem. ${\displaystyle q(\mu,\tau)=q(\mu)q(\tau)}$${\ Displaystyle \ mu}$${\ Displaystyle \ tau}$

Wyprowadzenie q(μ)

Następnie

${\ Displaystyle {\ zacząć {wyrównany} \ ln q_ {\ mu} ^ {*} (\ mu) & = \ nazwa operatora {e} _ {\ tau} \ lewo [\ ln p (\ mathbf {X} \ mid \mu ,\tau )+\ln p(\mu \mid \tau )+\ln p(\tau )\right]+C\\&=\nazwa operatora {E} _{\tau }\left[\ln p(\mathbf {X} \mid \mu ,\tau )\right]+\nazwa operatora {E} _{\tau }\left[\ln p(\mu \mid \tau )\right]+\nazwa operatora { E} _{\tau }\left[\ln p(\tau )\right]+C\\&=\nazwa operatora {E} _{\tau }\left[\ln \prod _{n=1}^ {N}{\mathcal {N}}\left(x_{n}\mid \mu ,\tau ^{-1}\right)\right]+\operatorname {E} _{\tau }\left[\ ln {\mathcal {N}}\left(\mu \mid \mu _{0},(\lambda _{0}\tau )^{-1}\right)\right]+C_{2}\\ &=\operatorname {E} _{\tau }\left[\ln \prod _{n=1}^{N}{\sqrt {\frac {\tau }{2\pi }}}e^{- {\frac {(x_{n}-\mu )^{2}\tau }{2}}}\right]+\nazwa operatora {E} _{\tau }\left[\ln {\sqrt {\frac {\lambda _{0}\tau }{2\pi }}}e^{-{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\tau }{ 2}}}\right]+C_{2}\\&=\nazwa operatora {E} _{\tau }\left[\sum _{n=1}^{N}\left({\frac {1} {2}}(\ln \tau -\ln 2\pi )-{\frac {(x_{n}-\mu )^{2}\tau }{2}}\rig ht)\right]+\nazwa operatora {E} _{\tau }\left[{\frac {1}{2}}(\ln \lambda _{0}+\ln \tau -\ln 2\pi ) -{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\tau }{2}}\right]+C_{2}\\&=\nazwa operatora {E} _{\tau }\left[\sum _{n=1}^{N}-{\frac {(x_{n}-\mu )^{2}\tau }{2}}\right]+\ nazwa operatora {E} _{\tau }\left[-{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\tau }{2}}\right]+\ nazwa operatora {E} _{\tau }\left[\sum _{n=1}^{N}{\frac {1}{2}}(\ln \tau -\ln 2\pi )\right]+ \operatorname {E} _{\tau }\left[{\frac {1}{2}}(\ln \lambda _{0}+\ln \tau -\ln 2\pi )\right]+C_{ 2}\\&=\nazwa operatora {E} _{\tau }\left[\sum _{n=1}^{N}-{\frac {(x_{n}-\mu )^{2}\ tau }{2}}\right]+\nazwa operatora {E} _{\tau }\left[-{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\ tau }{2}}\right]+C_{3}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{\sum _{ n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right\}+C_{ 3}\end{wyrównany}}}$

W powyższej pochodnej, , i odnoszą się do wartości, które są stałe w zakresie . Zauważ, że termin nie jest funkcją i będzie miał taką samą wartość niezależnie od wartości . Stąd w wierszu 3 możemy na końcu wchłonąć to w wyraz stały. To samo robimy w wierszu 7. ${\displaystyle C}$${\displaystyle C_{2}}$${\displaystyle C_{3}}$${\ Displaystyle \ mu}$${\ Displaystyle \ operatorname {E} _ {\ tau} [\ ln p (\ tau)]}$${\ Displaystyle \ mu}$${\ Displaystyle \ mu}$

Ostatni wiersz to po prostu wielomian kwadratowy w . Ponieważ jest to logarytm , możemy zobaczyć , że sam jest rozkładem Gaussa . ${\ Displaystyle \ mu}$${\ Displaystyle q_ {\ mu} ^ {*} (\ mu)}$${\ Displaystyle q_ {\ mu} ^ {*} (\ mu)}$

Z pewnej ilości żmudnej matematyki (rozszerzenie kwadraty wewnątrz szelki, rozdzielania i grupowania warunków obejmujących a i ukończenie kwadratowy over ), możemy czerpać parametry rozkładu Gaussa: ${\ Displaystyle \ mu}$${\ Displaystyle \ mu ^ {2}}$${\ Displaystyle \ mu}$

${\ Displaystyle {\ zacząć {wyrównany} \ ln q_ {\ mu } ^ {*} (\ mu) & = - {\ Frac {\ nazwa operatora {e} _ {\ tau} [\ tau]} {2}} \left\{\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2 }\right\}+C_{3}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{\sum _{n=1} ^{N}(x_{n}^{2}-2x_{n}\mu +\mu ^{2})+\lambda _{0}(\mu ^{2}-2\mu _{0} \mu +\mu _{0}^{2})\right\}+C_{3}\\&=-{\frac {\nazwa operatora {E} _{\tau }[\tau ]}{2} }\left\{\left(\sum _{n=1}^{N}x_{n}^{2}\right)-2\left(\sum _{n=1}^{N}x_{ n}\right)\mu +\left(\sum _{n=1}^{N}\mu ^{2}\right)+\lambda _{0}\mu ^{2}-2\lambda _ {0}\mu _{0}\mu +\lambda _{0}\mu _{0}^{2}\right\}+C_{3}\\&=-{\frac {\nazwa operatora {E } _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\mu ^{2}-2\left(\lambda _{0}\mu _{ 0}+\sum _{n=1}^{N}x_{n}\right)\mu +\left(\sum _{n=1}^{N}x_{n}^{2}\right )+\lambda _{0}\mu _{0}^{2}\right\}+C_{3}\\&=-{\frac {\nazwa operatora {E} _{\tau }[\tau ] }{2}}\left\{(\lambda _{0}+N)\mu ^{2}-2\left(\lambda _{0}\mu _{0}+\sum _{n=1 }^{N}x_{n}\right)\mu \right\}+C_{4}\\&=-{\frac {\ nazwa operatora {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\mu ^{2}-2\left({\frac {\lambda _ {0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)(\lambda _{0}+N )\mu \right\}+C_{4}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0 }+N)\left(\mu ^{2}-2\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n }}{\lambda _{0}+N}}\right)\mu \right)\right\}+C_{4}\\&=-{\frac {\nazwa operatora {E} _{\tau }[ \tau ]}{2}}\left\{(\lambda _{0}+N)\left(\mu ^{2}-2\left({\frac {\lambda _{0}\mu _{ 0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)\mu +\left({\frac {\lambda _{0} \mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}-\left({\frac { \lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}\right )\right\}+C_{4}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+ N)\left(\mu ^{2}-2\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}} {\lambda _{0}+N}}\right)\mu +\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_ {n}}{\lambda _{0}+N}}\prawo)^ {2}\right)\right\}+C_{5}\\&=-{\frac {\nazwa operatora {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\left(\mu -{\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}\right\}+C_{5}\\&=-{\frac {1}{2}}(\lambda _{0}+N)\ nazwa operatora {E} _{\tau }[\tau ]\left(\mu -{\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{ n}}{\lambda _{0}+N}}\right)^{2}+C_{5}\end{wyrównany}}}$

Zauważ, że wszystkie powyższe kroki można skrócić, używając wzoru na sumę dwóch kwadratów .

Innymi słowy:

${\ Displaystyle {\ zacząć {wyrównany} q_ {\ mu} ^ {*} (\ mu) i \ sim {\ mathcal {N}} (\ mu \ mid \ mu _ {N} \ lambda _ {N} ^{-1})\\\mu _{N}&={\frac {\lambda _{0}\mu _{0}+N{\bar {x}}}{\lambda _{0}+ N}}\\\lambda _{N}&=(\lambda _{0}+N)\nazwa operatora {E} _{\tau }[\tau ]\\{\bar {x}}&={\ frac {1}{N}}\sum _{n=1}^{N}x_{n}\end{wyrównany}}}$

Wyprowadzenie q(τ)

Wyprowadzenie jest podobne do powyższego, chociaż pomijamy niektóre szczegóły ze względu na zwięzłość. ${\ Displaystyle q_ {\ tau} ^ {*} (\ tau)}$

${\ Displaystyle {\ zacząć {wyrównany} \ ln q_ {\ tau} ^ {*} (\ tau) & = \ nazwa operatora {e} _ {\ mu} [\ ln p (\ mathbf {X} \ mid \ mu ,\tau )+\ln p(\mu \mid \tau )]+\ln p(\tau )+{\text{stała}}\\&=(a_{0}-1)\ln \tau - b_{0}\tau +{\frac {1}{2}}\ln \tau +{\frac {N}{2}}\ln \tau -{\frac {\tau }{2}}\nazwa operatora {E} _{\mu }\left[\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _ {0})^{2}\right]+{\text{stała}}\end{wyrównana}}}$

Potęgując obie strony, widzimy, że jest to rozkład gamma . Konkretnie: ${\ Displaystyle q_ {\ tau} ^ {*} (\ tau)}$

${\ Displaystyle {\ zacząć {wyrównany} q_ {\ tau} ^ {*} (\ tau) i \ sim \ operatorname {gamma} (\ tau \ mid a_ {N}, b_ {N}) \ \ a_ {N }&=a_{0}+{\frac {N+1}{2}}\\b_{N}&=b_{0}+{\frac {1}{2}}\nazwa operatora {E} _{ \mu }\left[\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^ {2}\right]\end{wyrównany}}}$

Algorytm obliczania parametrów

Podsumujmy wnioski z poprzednich rozdziałów:

${\ Displaystyle {\ zacząć {wyrównany} q_ {\ mu} ^ {*} (\ mu) i \ sim {\ mathcal {N}} (\ mu \ mid \ mu _ {N} \ lambda _ {N} ^{-1})\\\mu _{N}&={\frac {\lambda _{0}\mu _{0}+N{\bar {x}}}{\lambda _{0}+ N}}\\\lambda _{N}&=(\lambda _{0}+N)\nazwa operatora {E} _{\tau }[\tau ]\\{\bar {x}}&={\ frac {1}{N}}\sum _{n=1}^{N}x_{n}\end{wyrównany}}}$

oraz

${\ Displaystyle {\ zacząć {wyrównany} q_ {\ tau} ^ {*} (\ tau) i \ sim \ operatorname {gamma} (\ tau \ mid a_ {N}, b_ {N}) \ \ a_ {N }&=a_{0}+{\frac {N+1}{2}}\\b_{N}&=b_{0}+{\frac {1}{2}}\nazwa operatora {E} _{ \mu }\left[\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^ {2}\right]\end{wyrównany}}}$

W każdym przypadku parametry rozkładu po jednej ze zmiennych zależą od oczekiwań przyjętych względem drugiej zmiennej. Możemy rozszerzyć oczekiwania, korzystając ze standardowych wzorów na oczekiwania momentów rozkładu Gaussa i gamma:

${\ Displaystyle {\ zacząć {wyrównany} \ operatorname {E} [\ tau \ mid a_ {N}, b_ {N}] & = {\ Frac {a_ {N}} {b_ {N}}} \ \ \ nazwa operatora {E} \left[\mu \mid \mu _{N},\lambda _{N}^{-1}\right]&=\mu _{N}\\\nazwa operatora {E} \left[ X^{2}\right]&=\nazwa operatora {Var} (X)+(\nazwa operatora {E} [X])^{2}\\\nazwa operatora {E} \left[\mu ^{2}\ mid \mu _{N},\lambda _{N}^{-1}\right]&=\lambda _{N}^{-1}+\mu _{N}^{2}\end{wyrównany }}}$

Zastosowanie tych wzorów do powyższych równań jest w większości przypadków trywialne, ale równanie dla wymaga więcej pracy: ${\displaystyle b_{N}}$

${\ Displaystyle {\ zacząć {wyrównany} b_ {N} i = b_ {0}+ {\ Frac {1} {2}} \ operatorname {E} _ {\ mu} \ lewo [\ suma _ {n = 1 }^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right]\\&=b_{0 }+{\frac {1}{2}}\nazwa operatora {E} _{\mu }\left[(\lambda _{0}+N)\mu ^{2}-2\left(\lambda _{ 0}\mu _{0}+\sum _{n=1}^{N}x_{n}\right)\mu +\left(\sum _{n=1}^{N}x_{n} ^{2}\right)+\lambda _{0}\mu _{0}^{2}\right]\\&=b_{0}+{\frac {1}{2}}\left[( \lambda _{0}+N)\nazwa operatora {E} _{\mu }[\mu ^{2}]-2\left(\lambda _{0}\mu _{0}+\sum _{n =1}^{N}x_{n}\right)\operatorname {E} _{\mu }[\mu ]+\left(\sum _{n=1}^{N}x_{n}^{ 2}\right)+\lambda _{0}\mu _{0}^{2}\right]\\&=b_{0}+{\frac {1}{2}}\left[(\lambda _{0}+N)\left(\lambda _{N}^{-1}+\mu _{N}^{2}\right)-2\left(\lambda _{0}\mu _{ 0}+\sum _{n=1}^{N}x_{n}\right)\mu _{N}+\lewo(\sum _{n=1}^{N}x_{n}^{ 2}\right)+\lambda _{0}\mu _{0}^{2}\right]\\\end{aligned}}}$

Możemy wtedy zapisać równania parametrów w następujący sposób, bez żadnych oczekiwań:

${\ Displaystyle {\ zacząć {wyrównany} \ mu _ {N} i = {\ Frac {\ lambda _ {0} \ mu _ {0}+ N {\ bar {x}}} {\ lambda _ {0} +N}}\\\lambda _{N}&=(\lambda _{0}+N){\frac {a_{N}}{b_{N}}}\\{\bar {x}}& ={\frac {1}{N}}\sum _{n=1}^{N}x_{n}\\a_{N}&=a_{0}+{\frac {N+1}{2 }}\\b_{N}&=b_{0}+{\frac {1}{2}}\left[(\lambda _{0}+N)\left(\lambda _{N}^{- 1}+\mu _{N}^{2}\right)-2\left(\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n} \right)\mu _{N}+\left(\sum _{n=1}^{N}x_{n}^{2}\right)+\lambda _{0}\mu _{0}^ {2}\right]\end{wyrównany}}}$

Zauważ, że między formułami dla i istnieją zależności cykliczne . To naturalnie sugeruje algorytm podobny do EM : ${\ Displaystyle \ lambda _ {N}}$${\displaystyle b_{N}}$

1. Oblicz i użyj tych wartości do obliczenia i${\ Displaystyle \ suma _ {n = 1} ^ {N} x_ {n}}$${\ Displaystyle \ suma _ {n = 1} ^ {N} x_ {n} ^ {2}.}$${\ Displaystyle \ mu _ {N}}$${\ Displaystyle a_ {N}.}$
2. Zainicjuj do dowolnej wartości.${\ Displaystyle \ lambda _ {N}}$
3. Użyj bieżącej wartości wraz ze znanymi wartościami innych parametrów, aby obliczyć .${\ Displaystyle \ lambda _ {N},}$${\displaystyle b_{N}}$
4. Użyj bieżącej wartości wraz ze znanymi wartościami innych parametrów, aby obliczyć .${\displaystyle b_{N},}$${\ Displaystyle \ lambda _ {N}}$
5. Powtarzaj ostatnie dwa kroki aż do zbieżności (tj. dopóki żadna wartość nie zmieni się bardziej niż jakaś niewielka ilość).

Następnie mamy wartości hiperparametrów aproksymujących rozkładów parametrów a posteriori, których możemy użyć do obliczenia dowolnych właściwości a posteriori — np. jego średniej i wariancji, 95% obszaru o największej gęstości (najmniejszy przedział, który obejmuje 95 % całkowitego prawdopodobieństwa) itp.

Można wykazać, że ten algorytm gwarantuje zbieżność do lokalnego maksimum.

Należy również zauważyć, że rozkłady a posteriori mają taką samą formę jak odpowiadające im rozkłady wcześniejsze. Zrobiliśmy nie zakładamy tego; jedynym założeniem, jakie przyjęliśmy, było to, że rozkłady ulegają faktoryzacji, a forma rozkładów jest naturalna. Okazuje się (patrz niżej), że fakt, że rozkłady a posteriori mają taką samą postać jak rozkłady wcześniejsze, nie jest zbiegiem okoliczności, ale ogólnym wynikiem, gdy rozkłady poprzedzające należą do rodziny wykładniczej , co ma miejsce w większości przypadków standardowe dystrybucje.

Dalsza dyskusja

Przepis krok po kroku

Powyższy przykład pokazuje metodę, za pomocą której wyprowadza się aproksymację wariacyjną-bayesowską do gęstości prawdopodobieństwa a posteriori w danej sieci bayesowskiej :

1. Opisz sieć za pomocą modelu graficznego , identyfikując zmienne obserwowane (dane) i zmienne nieobserwowane ( parametry i zmienne latentne ) oraz ich warunkowe rozkłady prawdopodobieństwa . Następnie Bayes konstruuje przybliżenie prawdopodobieństwa a posteriori . Aproksymacja ma podstawową właściwość, że jest rozkładem faktoryzowanym, tj. iloczynem dwóch lub więcej rozkładów niezależnych przez rozłączne podzbiory zmiennych nieobserwowanych.${\ Displaystyle \ mathbf {X}}$ ${\displaystyle {\boldsymbol {\theta}}}$ ${\ Displaystyle \ mathbf {Z}}$${\ Displaystyle p (\ mathbf {Z} , {\ pogrubienie {\ Theta}} \ mid \ mathbf {X} )}$
2. Podziel nieobserwowane zmienne na dwa lub więcej podzbiorów, z których zostaną wyprowadzone niezależne czynniki. Nie ma uniwersalnej procedury, aby to zrobić; tworzenie zbyt wielu podzbiorów daje słabe przybliżenie, podczas gdy tworzenie zbyt małej liczby sprawia, że ​​cała wariacyjna procedura Bayesa jest niewykonalna. Zazwyczaj pierwszy podział polega na oddzieleniu parametrów i zmiennych ukrytych; często samo to wystarcza, aby uzyskać wykonalny wynik. Załóżmy, że partycje nazywają się .${\ Displaystyle \ mathbf {Z} _ {1} \ ldots \ mathbf {Z} _ {M}}$
3. Dla danego podziału zapisz wzór na najlepszy rozkład aproksymujący, korzystając z równania podstawowego .${\ Displaystyle \ mathbf {Z} _ {j}}$${\ Displaystyle q_ {j} ^ {*} (\ mathbf {Z} _ {j} \ mid \ mathbf {X})}$${\ Displaystyle \ ln q_ {j} ^ {*} (\ mathbf {Z} _ {j} \ mid \ mathbf {X} ) = \ operatorname {E} _ {i \ neq j} [\ ln p (\ mathbf {Z} ,\mathbf {X} )]+{\text{stała}}}$
4. Wypełnij wzór na łączny rozkład prawdopodobieństwa za pomocą modelu graficznego. Wszelkie rozkłady warunkowe składników, które nie obejmują żadnej ze zmiennych w, mogą zostać zignorowane; zostaną one złożone w stały termin.${\ Displaystyle \ mathbf {Z} _ {j}}$
5. Uprość formułę i zastosuj operator oczekiwania, zgodnie z powyższym przykładem. Idealnie, powinno to uprościć oczekiwanie podstawowych funkcji zmiennych, których nie ma (np. pierwszy lub drugi surowy moment , oczekiwanie logarytmu itp.). Aby wariacyjna procedura Bayesa działała dobrze, oczekiwania te powinny być ogólnie wyrażalne analitycznie jako funkcje parametrów i/lub hiperparametrów rozkładów tych zmiennych. We wszystkich przypadkach te warunki oczekiwania są stałymi w odniesieniu do zmiennych w bieżącym podziale.${\ Displaystyle \ mathbf {Z} _ {j}}$
6. Forma funkcjonalna wzoru w odniesieniu do zmiennych w aktualnym podziale wskazuje rodzaj rozkładu. W szczególności potęgowanie wzoru generuje funkcję gęstości prawdopodobieństwa (PDF) rozkładu (lub przynajmniej coś proporcjonalnego do niego, o nieznanej stałej normalizacji ). Aby cała metoda była wykonalna, powinno być możliwe rozpoznanie postaci funkcjonalnej jako należącej do znanego rozkładu. Konwersja formuły do ​​postaci zgodnej z plikiem PDF o znanej dystrybucji może wymagać znacznych manipulacji matematycznych. Gdy jest to możliwe, stałą normalizacji można przywrócić z definicji, a równania parametrów znanego rozkładu można wyprowadzić przez wyodrębnienie odpowiednich części wzoru.
7. Gdy wszystkie oczekiwania można zastąpić analitycznie funkcjami zmiennych spoza bieżącego podziału, a PDF umieścić w postaci umożliwiającej identyfikację ze znanym rozkładem, wynikiem jest zestaw równań wyrażających wartości optymalnych parametrów jako funkcje parametry zmiennych w innych przegrodach.
8. Gdy tę procedurę można zastosować do wszystkich partycji, wynikiem jest zestaw wzajemnie powiązanych równań określających optymalne wartości wszystkich parametrów.
9. Maksymalizację oczekiwań (EM) Procedura typ jest następnie nakładana, zbierając początkowej wartości dla każdego parametru oraz iteracja szeregu etapów, w których w każdym cyklu kroku poprzez równania, aktualizuje każdego parametru skrętu. Gwarantuje to zbieżność.

Najważniejsze punkty

Ze względu na wszystkie związane z tym manipulacje matematyczne, łatwo jest stracić orientację w dużym obrazie. Ważne rzeczy to:

1. Ideą wariacyjnego Bayesa jest skonstruowanie analitycznego przybliżenia prawdopodobieństwa a posteriori zbioru zmiennych nieobserwowanych (parametry i zmienne latentne) na podstawie danych. Oznacza to, że forma rozwiązania jest podobna do innych metod wnioskowania bayesowskiego , takich jak próbkowanie Gibbsa — czyli rozkład, który stara się opisać wszystko, co wiadomo o zmiennych. Podobnie jak w innych metodach bayesowskich — ale inaczej niż np. w metodzie maksymalizacji oczekiwań (EM) lub innych metodach największej wiarygodności — oba typy zmiennych nieobserwowanych (tj. parametry i zmienne latentne) są traktowane tak samo, tj. jako zmienne losowe . Szacunki dla zmiennych można następnie wyprowadzić standardowymi metodami bayesowskimi, np. obliczając średnią rozkładu w celu uzyskania jednopunktowego oszacowania lub wyprowadzając wiarygodny przedział , region o największej gęstości itp.
2. „Aproksymacja analityczna” oznacza, że ​​można zapisać wzór na rozkład a posteriori. Formuła zazwyczaj składa się z iloczynu dobrze znanych rozkładów prawdopodobieństwa, z których każdy jest faktoryzowany przez zestaw nieobserwowanych zmiennych (tzn. jest warunkowo niezależny od innych zmiennych, biorąc pod uwagę obserwowane dane). Ten wzór nie jest prawdziwym rozkładem a posteriori, ale jego przybliżeniem; w szczególności, będzie na ogół dość ściśle zgadzał się w najniższych momentach nieobserwowanych zmiennych, np. średniej i wariancji .
3. Wynikiem wszystkich manipulacji matematycznych jest (1) identyczność rozkładów prawdopodobieństwa składających się na czynniki oraz (2) wzajemnie zależne wzory na parametry tych rozkładów. Rzeczywiste wartości tych parametrów są obliczane numerycznie, poprzez naprzemienną procedurę iteracyjną, podobną do EM.

W porównaniu z maksymalizacją oczekiwań (EM)

Variation Bayes (VB) jest często porównywany z maksymalizacją oczekiwań (EM). Rzeczywista procedura numeryczna jest dość podobna, ponieważ obie są naprzemiennymi procedurami iteracyjnymi, które sukcesywnie zbliżają się do optymalnych wartości parametrów. Początkowe kroki w celu wyprowadzenia odpowiednich procedur są również niejasno podobne, oba zaczynają się od wzorów na gęstości prawdopodobieństwa i oba obejmują znaczne ilości manipulacji matematycznych.

Istnieje jednak szereg różnic. Najważniejsze jest to, co jest obliczane.

• EM oblicza estymatory punktowe rozkładu a posteriori tych zmiennych losowych, które można sklasyfikować jako „parametry”, ale tylko estymatory rzeczywistych rozkładów a posteriori zmiennych latentnych (przynajmniej w „miękkim EM”, a często tylko wtedy, gdy zmienne latentne są dyskretne ). Obliczone oceny punktowe są postaciami tych parametrów; brak innych informacji.
• Z drugiej strony VB oblicza oszacowania rzeczywistego rozkładu a posteriori wszystkich zmiennych, zarówno parametrów, jak i zmiennych latentnych. Gdy konieczne jest wyprowadzenie oszacowań punktowych, na ogół stosuje się średnią, a nie modę, jak jest to normalne we wnioskowaniu bayesowskim. W związku z tym parametry obliczone w VB nie mają takiego samego znaczenia jak te w EM. EM oblicza optymalne wartości parametrów samej sieci Bayesa. VB oblicza optymalne wartości parametrów rozkładów używanych do aproksymacji parametrów i zmiennych latentnych sieci Bayesa. Na przykład typowy model mieszaniny Gaussa będzie miał parametry dla średniej i wariancji każdego ze składników mieszaniny. EM bezpośrednio oszacowałoby optymalne wartości tych parametrów. Jednak VB najpierw dopasuje rozkład do tych parametrów — zazwyczaj w postaci wcześniejszego rozkładu , np. odwróconego rozkładu gamma o skali normalnej — a następnie obliczy wartości parametrów tego wcześniejszego rozkładu, tj. zasadniczo hiperparametrów . W tym przypadku VB obliczy optymalne oszacowania czterech parametrów odwróconego rozkładu gamma o skali normalnej, który opisuje łączny rozkład średniej i wariancji składnika.

Bardziej złożony przykład

Bayesowski model mieszaniny gaussowskiej z wykorzystaniem notacji płytowej . Mniejsze kwadraty oznaczają stałe parametry; większe kółka oznaczają zmienne losowe. Wypełnione kształty wskazują znane wartości. Oznaczenie [K] oznacza wektor o rozmiarze K ; [ D , D ] oznacza macierz o rozmiarze D × D ; Samo K oznacza zmienną kategorialną z wynikami K. Falista linia wychodząca od z kończącego się poprzeczką wskazuje przełącznik — wartość tej zmiennej wybiera dla innych przychodzących zmiennych, którą wartość użyć z tablicy size- K możliwych wartości.

Wyobraźmy sobie model mieszanki bayesowskiej Gaussa opisany w następujący sposób:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {\ pi} i \ sim \ operatorname {SymDir} (K, \ alfa _ {0}) \ \ \ mathbf {\ Lambda} _ {i = 1 \ kropki K} &\sim {\mathcal {W}}(\mathbf {W} _{0},\nu _{0})\\\mathbf {\mu } _{i=1\dots K}&\sim {\ mathcal {N}}(\mathbf {\mu } _{0},(\beta _{0}\mathbf {\Lambda } _{i})^{-1})\\\mathbf {z} [i =1\dots N]&\sim \operatorname {Mult} (1,\mathbf {\pi } )\\\mathbf {x} _{i=1\dots N}&\sim {\mathcal {N}} (\mathbf {\mu } _{z_{i}},{\mathbf {\Lambda } _{z_{i}}}^{-1})\\K&={\text{liczba składników mieszających}} \\N&={\text{liczba punktów danych}}\end{wyrównany}}}$

Notatka:

• SymDir() jest symetrycznym rozkładem Dirichleta wymiaru , z hiperparametrem dla każdego komponentu ustawionym na . Rozkład Dirichlet jest koniugat przed z rozkładu kategorycznego lub podziału wielomianu .${\ Displaystyle K}$${\ Displaystyle \ alfa _ {0}}$
• ${\displaystyle {\mathcal {W}}()}$jest rozkładem Wisharta , który jest sprzężoną przed macierzą precyzji ( macierz odwrotnej kowariancji ) dla wielowymiarowego rozkładu Gaussa .
• Mult() to rozkład wielomianowy na pojedynczej obserwacji (odpowiednik rozkładu kategorycznego ). Przestrzeń stanów jest reprezentacją „jeden z K”, tj. wektorem dwuwymiarowym, w którym jeden z elementów ma wartość 1 (określającą identyczność obserwacji), a wszystkie pozostałe 0.${\ Displaystyle K}$
• ${\displaystyle {\mathcal {N}}()}$jest rozkładem Gaussa , w tym przypadku konkretnie wielowymiarowym rozkładem Gaussa .

Interpretacja powyższych zmiennych jest następująca:

• ${\ Displaystyle \ mathbf {X} = \ {\ mathbf {x} _ {1} \ kropki \ mathbf {x} _ {N} \}}$to zbiór punktów danych, z których każdy jest wektorem dwuwymiarowym rozłożonym zgodnie z wielowymiarowym rozkładem Gaussa .${\ Displaystyle N}$${\ Displaystyle D}$
• ${\ Displaystyle \ mathbf {Z} = \ {\ mathbf {z} _ {1}, \ kropki, \ mathbf {z} _ {N} \}}$to zestaw zmiennych ukrytych, po jednej na punkt danych, określający, do którego składnika mieszaniny należy odpowiedni punkt danych, przy użyciu reprezentacji wektorowej „jeden z K” ze składnikami dla , jak opisano powyżej.${\displaystyle z_{nk}}$${\ Displaystyle k = 1 \ kropki K}$
• ${\displaystyle \mathbf {\pi}}$to proporcje mieszania składników mieszanki.${\ Displaystyle K}$
• ${\ Displaystyle \ mathbf {\ mu} _ {i = 1 \ kropki K}}$i określić parametry ( średnia i precyzja ) związane z każdym składnikiem mieszaniny.${\ Displaystyle \ mathbf {\ Lambda} _ {i = 1 \ kropki K}}$

Wspólne prawdopodobieństwo wszystkich zmiennych można przepisać jako

${\ Displaystyle p (\ mathbf {X} , \ mathbf {Z} , \ mathbf {\ pi} , \ mathbf {\ mu} , \ mathbf {\ Lambda} ) = p (\ mathbf {X} \ mid \ mathbf {Z} ,\mathbf {\mu } ,\mathbf {\Lambda } )p(\mathbf {Z} \mid \mathbf {\pi } )p(\mathbf {\pi } )p(\mathbf {\mu } \mid \mathbf {\Lambda } )p(\mathbf {\Lambda } )}$

gdzie znajdują się poszczególne czynniki

${\ Displaystyle {\ zacząć {wyrównany} p (\ mathbf {X} \ mid \ mathbf {Z}, \ mathbf {\ mu}, \ mathbf {\ Lambda} ) & = \ prod _ {n = 1} ^ { N}\prod _{k=1}^{K}{\mathcal {N}}(\mathbf {x} _{n}\mid \mathbf {\mu } _{k},\mathbf {\Lambda } _{k}^{-1})^{z_{nk}}\\p(\mathbf {Z} \mid \mathbf {\pi } )&=\prod _{n=1}^{N}\ prod _{k=1}^{K}\pi _{k}^{z_{nk}}\\p(\mathbf {\pi } )&={\frac {\Gamma (K\alpha _{0 })}{\Gamma (\alpha _{0})^{K}}}\prod _{k=1}^{K}\pi _{k}^{\alpha _{0}-1}\ \p(\mathbf {\mu } \mid \mathbf {\Lambda } )&=\prod _{k=1}^{K}{\mathcal {N}}(\mathbf {\mu } _{k} \mid \mathbf {\mu } _{0},(\beta _{0}\mathbf {\Lambda } _{k})^{-1})\\p(\mathbf {\Lambda } )&= \prod _{k=1}^{K}{\mathcal {W}}(\mathbf {\Lambda } _{k}\mid \mathbf {W} _{0},\nu _{0})\ koniec{wyrównany}}}$