Zasada włączenia-wykluczenia - Inclusion–exclusion principle

W kombinatoryce , gałęzi matematyki , zasada włączenia-wykluczenia jest techniką liczenia, która uogólnia znaną metodę uzyskiwania liczby elementów w związku dwóch zbiorów skończonych ; symbolicznie wyrażone jako

${\ Displaystyle | A \ filiżanka B | = | A | + | B | - | A \ czapka B |,}$

gdzie A i B są dwoma zbiorami skończonymi i | S | wskazuje liczność zbioru S (którą można uznać za liczbę elementów zbioru, jeśli zbiór jest skończony ). Wzór wyraża fakt, że suma rozmiarów dwóch zestawów może być zbyt duża, ponieważ niektóre elementy mogą być liczone dwukrotnie. Elementy liczone podwójnie to te, które znajdują się na przecięciu dwóch zestawów, a liczba jest korygowana przez odjęcie rozmiaru przecięcia.

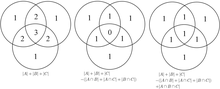
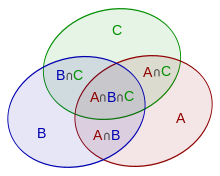
Zasada inkluzji-wykluczenia, będąca uogólnieniem przypadku dwuzbiorowego, jest chyba wyraźniej widoczna w przypadku zbiorów trzech, co dla zbiorów A , B i C dana jest wzorem

${\ Displaystyle | A \ filiżanka B \ filiżanka C | = | A | + | B | + | C | - | A \ czapka B | - | A \ czapka C | - | B \ czapka C | + | A \ czapka B\cap C|.}$

Ten wzór można zweryfikować, licząc, ile razy każdy region na diagramie Venna jest uwzględniony po prawej stronie wzoru. W tym przypadku, przy usuwaniu wkładów przeliczonych elementów, liczba elementów we wzajemnym przecięciu trzech zestawów była zbyt często odejmowana, więc należy ją dodać z powrotem, aby uzyskać poprawną sumę.

Uogólnienie wyników tych przykładów daje zasadę włączenia-wykluczenia. Aby znaleźć liczność sumy n zbiorów:

1. Uwzględnij moce zestawów.
2. Wyklucz moce przecięć parami.
3. Uwzględnij moce potrójnych skrzyżowań.
4. Wyklucz moce poczwórnych skrzyżowań.
5. Uwzględnij moce pięciokrotnych skrzyżowań.
6. Kontynuuj, aż liczność n -krotnego przecięcia zostanie uwzględniona (jeśli n jest nieparzyste) lub wyłączone ( n parzyste).

Nazwa wzięła się od idei, że zasada opiera się na nadmiernym włączeniu , a następnie kompensacyjnym wykluczeniu . Koncepcję tę przypisuje się Abrahamowi de Moivre (1718); ale po raz pierwszy pojawia się w artykule Daniela da Silvy (1854), a później w artykule JJ Sylwestra (1883). Czasem zasadę tę nazywa się formułą Da Silvy lub Sylwestra ze względu na te publikacje. Zasada jest przykładem metody sitowej szeroko stosowanej w teorii liczb i jest czasami określana jako formuła sitowa , chociaż Legendre już używał podobnego urządzenia w kontekście sitowym w 1808 roku.

Ponieważ skończone prawdopodobieństwa są obliczane jako zliczenia względem liczności przestrzeni prawdopodobieństwa , wzory na zasadę włączania-wykluczania pozostają ważne, gdy moce zbiorów są zastępowane skończonymi prawdopodobieństwami. Bardziej ogólnie, obie wersje zasady można umieścić pod wspólnym parasolem teorii miary .

W bardzo abstrakcyjnym otoczeniu zasada włączenia-wykluczenia może być wyrażona jako obliczenie odwrotności pewnej macierzy. Ta odwrotność ma specjalną strukturę, dzięki czemu zasada ta jest niezwykle cenną techniką w kombinatoryce i pokrewnych dziedzinach matematyki. Jak ujął to Gian-Carlo Rota :

„Jedną z najbardziej użytecznych zasad wyliczania w prawdopodobieństwie dyskretnym i teorii kombinatorycznej jest słynna zasada włączenia-wykluczenia. Umiejętnie zastosowana zasada ta przyniosła rozwiązanie wielu problemów kombinatorycznych”.

Oświadczenie

W swej ogólnej postaci zasada inkluzji-wykluczenia głosi, że dla zbiorów skończonych A ₁ , ..., A _n , mamy identyczność

${\ Displaystyle \ lewo | \ bigcup _ {i = 1} ^ {n} A_ {i} \ po prawej | = \ suma _ {i = 1} ^ {n} | A_ {i} | - \ suma _ {1 \leqslant i<j\leqslant n}|A_{i}\cap A_{j}|+\sum _{1\leqslant i<j<k\leqslant n}|A_{i}\cap A_{j}\ cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.}$

( 1 )

Można to zwięźle zapisać jako

${\ Displaystyle \ lewo | \ bigcup _ {i = 1} ^ {n} A_ {i} \ po prawej | = \ suma _ {k = 1} ^ {n} (-1) ^ {k + 1} \ po lewej (\sum _{1\leqslant i_{1}<\cdots <i_{k}\leqslant n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)}$

lub

${\ Displaystyle \ lewo | \ bigcup _ {i = 1} ^ {n} A_ {i} \ prawej | = \ suma _ {\ pusty zbiór \ neq J \ subseteq \ {1, \ ldots, n \}} (- 1)^{|J|+1}\left|\bigcap _{j\in J}A_{j}\right|.}$

Mówiąc słownie, aby policzyć liczbę elementów w skończonej unii zbiorów skończonych, najpierw zsumuj moce poszczególnych zbiorów, następnie odejmij liczbę elementów, które pojawiają się w co najmniej dwóch zestawach, a następnie dodaj z powrotem liczbę elementów, które pojawiają się w co najmniej trzy zestawy, a następnie odejmij liczbę elementów, które pojawiają się w co najmniej czterech zestawach i tak dalej. Ten proces zawsze się kończy, ponieważ nie może być elementów, które pojawiają się w większej liczbie zestawów niż liczba zestawów w unii. (Na przykład, jeśli nie może być elementów, które występują w więcej niż zestawach; równoważnie, nie może być elementów, które występują w co najmniej zestawach). ${\displaystyle n=4,}$${\ Displaystyle 4}$${\ Displaystyle 5}$

W zastosowaniach często spotyka się zasadę wyrażoną w formie uzupełniającej. Oznacza to, że niech S będzie skończonym zbiorem uniwersalnym zawierającym wszystkie A _i i niech oznacza dopełnienie A _i w S , zgodnie z prawami De Morgana mamy ${\ Displaystyle {\ bar {A_ {i}}}}$

${\ Displaystyle \ lewo | \ bigcap _ {i = 1} ^ {n} {\ bar {A_ {i}}} \ prawo | = \ lewo | S- \ bigcup _ {i = 1} ^ {n} A_ {i}\right|=|S|-\sum _{i=1}^{n}|A_{i}|+\sum _{1\leqslant i<j\leqslant n}|A_{i}\ cap A_{j}|-\cdots +(-1)^{n}|A_{1}\cap \cdots \cap A_{n}|.}$

Jako inny wariant twierdzenia, niech P ₁ , ..., P _n będzie listą własności, które elementy zbioru S mogą mieć lub nie, to zasada włączenia-wykluczenia pozwala obliczyć liczbę elementów z S , który ma żadnej właściwości. Po prostu niech A _i będzie podzbiorem elementów S, które mają własność Pi _i używają zasady w jej komplementarnej formie. Ten wariant to zasługa JJ Sylwestra .

Zauważ, że jeśli weźmiesz pod uwagę tylko pierwszych m<n sum po prawej stronie (w ogólnej postaci zasady), otrzymasz przeszacowanie, jeśli m jest nieparzyste, a niedoszacowanie, jeśli m jest parzyste.

Przykłady

Liczenie liczb całkowitych

Jako prosty przykład zastosowania zasady włączenia-wykluczenia rozważ pytanie:

Ile liczb całkowitych w {1,...,100} nie jest podzielnych przez 2, 3 lub 5?

Niech S = {1,...,100} i P ₁ własność, że liczba całkowita jest podzielna przez 2, P ₂ własność, że liczba całkowita jest podzielna przez 3, a P ₃ własność, że liczba całkowita jest podzielna przez 5. A _i będzie podzbiorem S, którego elementy mają własność P _i otrzymamy przez elementarne liczenie: | ₁ | = 50, | ₂ | = 33, oraz | ₃ | = 20. Jest 16 takich liczb całkowitych podzielnych przez 6, 10 podzielnych przez 10 i 6 podzielnych przez 15. W końcu są tylko 3 liczby całkowite podzielne przez 30, więc liczba liczb całkowitych niepodzielnych przez żadną z 2, 3 lub 5 jest dany przez:

100 − (50 + 33 + 20) + (16 + 10 + 6) - 3 = 26.

Liczenie zaburzeń

Bardziej złożony przykład jest następujący.

Załóżmy, że istnieje talia składająca się z n kart ponumerowanych od 1 do  n . Załóżmy, że karta o numerze m znajduje się we właściwej pozycji, jeśli jest m- tą kartą w talii. Na ile sposobów, W , można potasować karty, gdy co najmniej 1 karta znajduje się we właściwej pozycji?

Rozpocznij od zdefiniowania zbioru A _m , czyli wszystkich kolejności kart z poprawną m- tą kartą. Wtedy liczba rozkazów W , z co najmniej jedną kartą znajdującą się we właściwej pozycji, m , wynosi

${\ Displaystyle W = \ lewo | \ bigcup _ {m = 1} ^ {n} A_ {m} \ prawo |.}$

Stosować zasadę inkluzji-wykluczenia,

${\ Displaystyle W = \ suma _ {m_ {1} = 1} ^ {n} | A_ {m_ {1}} | - \ suma _ {1 \ leqslant m_ {1} < m_ {2} \ leqslant n} |A_{m_{1}}\cap A_{m_{2}}|+\cdots +(-1)^{p-1}\sum _{1\leqslant m_{1}<\cdots <m_{p }\leqslant n}|A_{m_{1}}\cap \cdots \cap A_{m_{p}}|+\cdots }$

Każda wartość przedstawia zespół tasowania mających co najmniej P wartości m ₁ , ...,  m, _p we właściwym położeniu. Zauważ, że liczba przetasowań z co najmniej poprawnymi wartościami p zależy tylko od p , a nie od poszczególnych wartości . Na przykład, liczba tasowania z 1., 3. i 17. kartą we właściwej pozycji jest taka sama, jak liczba tasowania z 2., 5. i 13. kartą we właściwych pozycjach. Liczy się tylko to, że z n kart 3 zostały wybrane, aby znaleźć się we właściwej pozycji. Zatem w sumowaniu p występują równe warunki (patrz kombinacja ). ${\ Displaystyle A_ {m_ {1}} \ czapka \ cdots \ czapka A_ {m_ {p}}}$${\ Displaystyle m}$${\displaystyle {n \wybierz p}}$

${\ Displaystyle W = {n \ wybrać 1} | A_ {1} | - {n \ wybrać 2} | A_ {1} \ czapka A_ {2} | + \ cdots + (-1) ^ {p-1} {n \choose p}|A_{1}\cap \cdots \cap A_{p}|+\cdots }$

${\ Displaystyle | A_ {1} \ czapka \ cdots \ czapka A_ {p} |}$to liczba uporządkowań mających p elementów we właściwej pozycji, która jest równa liczbie sposobów uporządkowania pozostałych n  −  p elementów, czyli ( n  −  p )!. W ten sposób w końcu otrzymujemy:

${\ Displaystyle {\ zacząć {wyrównany} W & = {n \ wybrać 1} (n-1)! - {n \ wybrać 2} (n-2)! + \ cdots + (-1) ^ {p-1} {n \wybierz p}(np)!+\cdots \\&=\sum _{p=1}^{n}(-1)^{p-1}{n \wybierz p}(np)!\ \&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!(np)!}}(np)!\\&=\ suma _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!}}\end{wyrównane}}}$

Permutacja, w której żadna karta nie znajduje się we właściwej pozycji, nazywana jest obłąkaniem . Biorąc n ! aby być całkowitą liczbą permutacji, prawdopodobieństwo Q, że losowe przetasowanie spowoduje zaburzenie jest dane przez

${\ Displaystyle Q = 1- {\ Frac {W} {n!}} = \ suma _ {p = 0} ^ {n} {\ Frac {(-1) ^ {p}} {p!}}, }$

przycięcie na n  + 1 względem rozwinięcia Taylora z E ^-1 . Zatem prawdopodobieństwo odgadnięcia kolejności dla potasowanej talii kart i błędnego określenia każdej karty wynosi około e- ¹ lub 37%.

Szczególny przypadek

Sytuacja, która pojawia się w powyższym przykładzie z zaburzeniami, występuje na tyle często, że zasługuje na szczególną uwagę. Mianowicie, gdy wielkość zbiorów przecięcia występujących we wzorach na zasadę włączenia-wykluczenia zależy tylko od liczby zbiorów w przecięciach, a nie od tego, które zbiory się pojawiają. Bardziej formalnie, jeśli skrzyżowanie

${\ Displaystyle A_ {J}: = \ bigcap _ {j \ w J} A_ {j}}$

ma taką samą moc, powiedzmy α _k = | A _J |, dla każdego k- elementowego podzbioru J z {1, ...,  n }, to

${\ Displaystyle \ lewo | \ bigcup _ {i = 1} ^ {n} A_ {i} \ prawej | = \ suma _ {k = 1} ^ {n} (-1) ^ {k-1} {\ binom {n}{k}}\alfa _{k}.}$

Lub w formie komplementarnej, gdzie zbiór uniwersalny S ma moc α ₀ ,

${\ Displaystyle \ lewo | S \ setminus \ bigcup _ {i = 1} ^ {n} A_ {i} \ prawo | = \ suma _ {k = 0} ^ {n} (-1) ^ {k} \binom {n}{k}}\alfa _{k}.}$

Uogólnienie

Mając rodzinę (dozwolone powtórzenia) podzbiorów A ₁ , A ₂ , ..., A _n zbioru uniwersalnego S , zasada włączenia-wykluczenia nie oblicza liczby elementów S w żadnym z tych podzbiorów. Uogólnienie tego pojęcia pozwoliłoby obliczyć liczbę elementów S, które występują w dokładnie pewnym ustalonym m tych zbiorów.

Niech N = [ n ] = {1,2,..., n }. Jeśli zdefiniujemy , to zasadę włączenia-wykluczenia można zapisać jako, używając notacji z poprzedniego podrozdziału; liczba elementów S zawartych w żadnym z A _i wynosi: ${\ Displaystyle A_ {\ Emptyset} = S}$

${\ Displaystyle \ suma _ {J \ subseteq [n]} (-1) ^ {| J |} | A_ {J} |.}$

Jeżeli I jest ustalonym podzbiorem zbioru indeksów N , to liczba elementów należących do A _i dla wszystkich i w I i dla żadnych innych wartości wynosi:

${\ Displaystyle \ suma _ {I \ subseteq J} (-1) ^ {| J | - | I |} | A_ {J} |.}$

Zdefiniuj zestawy

${\ Displaystyle B_ {k} = A_ {ja \ filiżanka \ {k \}} {\ tekst {dla}} k \ w N \ setminus I.}$

Poszukujemy liczby elementów w żadnym z B _k, które zgodnie z zasadą włączenia-wykluczenia (z ) wynosi ${\ Displaystyle B_ {\ Emptyset} = A_ {I}}$

${\ Displaystyle \ suma _ {K \ subseteq N \ setminus I} (-1) ^ {| K |} | B_ {K} |.}$

Korespondencja K ↔ J = I ∪ K między podzbiorami N  \  I a podzbiorami N zawierającymi I jest bijekcją i jeśli J i K odpowiadają sobie pod tą mapą, to B _K = A _J , co pokazuje, że wynik jest poprawny.

W prawdopodobieństwie

W prawdopodobieństwie , dla zdarzeń A ₁ , ..., A _n w przestrzeni prawdopodobieństwa , zasada włączenia-wykluczenia staje się dla n  = 2 ${\ Displaystyle \ scriptstyle (\ Omega {\ mathcal {F}} \ mathbb {P})}$

${\ Displaystyle \ mathbb {P} (A_ {1} \ filiżanka A_ {2}) = \ mathbb {P} (A_ {1}) + \ mathbb {P} (A_ {2}) - \ mathbb {P} (A_{1}\cap A_{2}),}$

dla n  = 3

${\ Displaystyle \ mathbb {P} (A_ {1} \ filiżanka A_ {2} \ filiżanka A_ {3}) = \ mathbb {P} (A_ {1}) + \ mathbb {P} (A_ {2}) +\mathbb {P} (A_{3})-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\ mathbb {P} (A_{2}\cap A_{3})+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})}$

i na ogół

${\ Displaystyle \ mathbb {P} \ lewo (\ bigcup _ {i = 1} ^ {n} A_ {i} \ prawej) = \ suma _ {i = 1} ^ {n} \ mathbb {P} (A_ {i})-\sum _{i<j}\mathbb {P} (A_{i}\cap A_{j})+\sum _{i<j<k}\mathbb {P} (A_{i }\cap A_{j}\cap A_{k})+\cdots +(-1)^{n-1}\sum _{i<...<n}\mathbb {P} \left(\bigcap _{i=1}^{n}A_{i}\prawo),}$

które można zapisać w formie zamkniętej jako

${\ Displaystyle \ mathbb {P} \ lewo (\ bigcup _ {i = 1} ^ {n} A_ {i} \ prawej) = \ suma _ {k = 1} ^ {n} \ lewo ((-1) ^{k-1}\sum _{I\subseteq \{1,\ldots ,n\} \atop |I|=k}\mathbb {P} (A_{I})\right),}$

gdzie ostatnia suma przebiega przez wszystkie podzbiory I indeksów 1, ..., n, które zawierają dokładnie k elementów, oraz

${\ Displaystyle A_ {I}: = \ bigcap _ {i \ w I} A_ {i}}$

oznacza przecięcie wszystkich tych A _i z indeksem w I .

Zgodnie z nierównościami Bonferroniego suma pierwszych członów we wzorze stanowi na przemian górną i dolną granicę dla LHS . Można to wykorzystać w przypadkach, gdy pełna formuła jest zbyt uciążliwa.

Dla ogólnej przestrzeni miary ( S ,Σ, μ ) i mierzalnych podzbiorów A ₁ , ..., A _n skończonej miary, powyższe tożsamości zachowują się również wtedy, gdy miara prawdopodobieństwa zostaje zastąpiona miarą μ . ${\ Displaystyle \ mathbb {P}}$

Szczególny przypadek

Jeżeli w probabilistycznej wersji zasada włączeń i wyłączeń, prawdopodobieństwo przecięcia _I zależy tylko od liczności I , co oznacza, że dla każdego k w {1, ...,  n } istnieje _k takie, że

${\ Displaystyle a_ {k} = \ mathbb {P} (A_ {ja}) {\ tekst {dla każdego}} ja \ podzbiór \ {1, \ ldots, n \} {\ tekst {z}} | ja | =k,}$

to powyższy wzór upraszcza się do

${\ Displaystyle \ mathbb {P} \ lewo (\ bigcup _ {i = 1} ^ {n} A_ {i} \ prawej) = \ suma _ {k = 1} ^ {n} (-1) ^ {k -1}{\binom {n}{k}}a_{k}}$

ze względu na kombinatoryczną interpretację współczynnika dwumianowego . Na przykład, jeśli zdarzenia są niezależne i identycznie rozłożone , to dla wszystkich i , a mamy , w takim przypadku powyższe wyrażenie upraszcza się do ${\displaystyle \scriptstyle {\binom {n}{k}}}$${\ Displaystyle A_ {i}}$${\ Displaystyle \ mathbb {P} (A_ {i}) = p}$${\ Displaystyle a_ {k} = p ^ {k}}$

${\ Displaystyle \ mathbb {P} \ lewo (\ bigcup _ {i = 1} ^ {n} A_ {i} \ prawej) = 1 - (1-p) ^ {n}.}$

(Wynik ten można również uzyskać w prostszy sposób, biorąc pod uwagę przecięcie się dopełnień wydarzeń .) ${\ Displaystyle A_ {i}}$

Analogiczne uproszczenie jest możliwe w przypadku ogólnej przestrzeni miar ( S ,Σ, μ ) i mierzalnych podzbiorów A ₁ , ..., A _n o skończonej miary.

Inne formy

Zasada jest czasami wyrażana w formie, która mówi, że jeśli

${\ Displaystyle g (A) = \ suma _ {S \ podseteq A} f (S)}$

następnie

${\ Displaystyle f (A) = \ suma _ {S \ podseteq A} (-1) ^ {| A | - | S |} g (S) \ qquad (**)}$

Kombinatoryczna i probabilistyczna wersja zasady włączenia-wykluczenia są przykładami (**).

Jeśli ktoś postrzega liczbę jako zbiór jej czynników pierwszych, to (**) jest uogólnieniem wzoru inwersji Möbiusa dla liczb naturalnych bez kwadratów . Dlatego, (**) jest uważana za wzorze inwersji Möbius do Algebra padania na częściowy porządek wszystkich podgrup A . ${\ Displaystyle n}$

Aby uogólnić pełną wersję formuły inwersji Möbiusa, (**) należy uogólnić do multisets . Dla multisetów zamiast zestawów, (**) staje się

${\ Displaystyle f (A) = \ suma _ {S \ podseteq A} \ mu (AS) g (S) \ qquad (***)}$

gdzie jest multiset dla którego , i ${\displaystyle AS}$${\ Displaystyle (AS) \ plus S = A}$

• μ ( S ) = 1 jeśli S jest zbiorem (tj. zbiorem wieloelementowym bez elementów podwójnych) o parzystej liczności .
• μ ( S ) = -1 jeśli S jest zbiorem (tj. zbiorem wieloelementowym bez elementów podwójnych) o nieparzystej liczności.
• μ ( S ) = 0 jeśli S jest prawidłowym multisetem (tzn. S ma elementy podwójne).

Zauważ, że jest to tylko (**) w przypadku, gdy jest to zestaw. ${\ Displaystyle \ mu (jako)}$${\ Displaystyle (-1) ^ {| A | - | S |}}$${\displaystyle AS}$

Aplikacje

Zasada włączenia-wykluczenia jest szeroko stosowana i tylko kilka z jej zastosowań można tu wymienić.

Liczenie zaburzeń

Dobrze znanym zastosowaniem zasady inkluzji i wykluczenia jest kombinatoryczny problem liczenia wszystkich odchyleń zbioru skończonego. Derangement z ustalonym A to bijection od A do siebie, że nie ma stałych punktów. Za pomocą zasady włączenia-wykluczenia można wykazać, że jeśli liczność A wynosi n , to liczba odchyleń wynosi [ n ! /  e ] gdzie [ x ] oznacza najbliższą liczbę całkowitą do x ; szczegółowy dowód jest dostępny tutaj, a także zobacz sekcję przykładów powyżej.

Problem z liczeniem derangementów pojawił się po raz pierwszy we wczesnej książce o grach losowych: Essai d'analyse sur les jeux de hazard autorstwa PR de Montmort (1678 – 1719) i był znany jako „problem Montmorta” lub przez imię, które mu nadał, „ problème des rencontres ”. Problem jest również znany jako problem sprawdzania kapelusza.

Liczba zaburzeniami jest również znany jako subfactorial z n , napisany! n . Wynika z tego, że jeśli wszystkim bijekcjom przypisuje się to samo prawdopodobieństwo, to prawdopodobieństwo, że losowa bijekcja jest zaburzeniem, szybko zbliża się do 1/ e, gdy n rośnie.

Liczenie skrzyżowań

Zasada inkluzji-wykluczenia w połączeniu z prawem De Morgana może być również użyta do obliczenia liczności przecięcia zbiorów. Niech reprezentuj dopełnienie A _k względem pewnego zbioru uniwersalnego A takiego, że dla każdego k . Potem będzie ${\ Displaystyle {\ overline {A_ {k}}}}$${\ Displaystyle A_ {k} \ podseteq A}$

${\ Displaystyle \ bigcap _ {i = 1} ^ {n} A_ {i} = {\ overline {\ bigcup _ {i = 1} ^ {n} {\ overline {A_ {i}}}}}}$

tym samym zamieniając problem znalezienia skrzyżowania w problem znalezienia związku.

Kolorowanie wykresu

Zasada wykluczania inkluzji stanowi podstawę algorytmów dla wielu problemów z partycjonowaniem NP-twardych grafów, takich jak kolorowanie grafów.

Dobrze znanym zastosowaniem tej zasady jest konstrukcja wielomianu chromatycznego grafu.

Wykres dwudzielny idealne dopasowania

Liczba doskonałych skojarzeń o dwustronnym wykresu można obliczyć stosując zasadę.

Liczba na funkcji

Biorąc pod uwagę zbiory skończone A i B , ile jest funkcji surjektywnych (na funkcje) od A do B ? Bez utraty ogólności możemy przyjąć A = {1, ..., k } i B = {1, ..., n }, ponieważ liczą się tylko moce zbiorów. Używając S jako zbioru wszystkich funkcji od A do B i definiując, dla każdego i w B , właściwość P _i jako „funkcja pomija element i w B ” ( i nie znajduje się na obrazie funkcji), zasada inkluzji-wykluczenia podaje liczbę funkcji on między A i B jako:

${\ Displaystyle \ suma _ {j = 0} ^ {n} {\ Binom {n} {j}} (-1) ^ {j} (nj) ^ {k}.}$

Permutacje z zabronionymi pozycjami

Permutacją zbioru S = {1, ..., N }, gdzie każdy element S jest ograniczona do nie być w pewnych pozycjach (tutaj permutacji jest uważany za uporządkowania elementów S ) nazywa się permutacji zabronione pozycje . Na przykład, przy S = {1,2,3,4}, permutacje z ograniczeniem, że element 1 nie może znajdować się na pozycjach 1 lub 3, a element 2 nie może być na pozycji 4 to: 2134, 2143, 3124, 4123, 2341, 2431, 3241, 3421, 4231 i 4321. Pozwalając, aby A _i był zbiorem pozycji, w których element i nie może się znajdować, a właściwość P _i jest własnością, w której permutacja umieszcza element i na pozycję w A _i , zasada włączenia-wykluczenia może być użyta do obliczenia liczby permutacji, które spełniają wszystkie ograniczenia.

W podanym przykładzie mamy 12 = 2(3!) permutacji o własności P ₁ , 6 = 3! permutacje z właściwością P ₂ i żadne permutacje mają właściwości P ₃ lub P _4, ponieważ nie ma ograniczeń dla tych dwóch elementów. Liczba permutacji spełniających ograniczenia wynosi zatem:

4! − (12 + 6 + 0 + 0) + (4) = 24 − 18 + 4 = 10.

Ostatnia 4 w tym obliczeniu to liczba permutacji mających obie właściwości P ₁ i P ₂ . Nie ma innych niezerowych wkładów do formuły.

Liczby Stirlinga drugiego rodzaju

Te numery Stirlinga drugiego rodzaju , S ( n , k ) zliczania liczby partycji, z zestawem n elementów w k niepusty podgrup (odróżnienia pudełka ). Wyraźny dla nich wzór można uzyskać, stosując zasadę włączania-wykluczania do bardzo ściśle powiązanego problemu, a mianowicie liczenia liczby podziałów zbioru n na k niepustych, ale rozróżnialnych pól ( uporządkowanych niepustych podzbiorów) . Używając uniwersalnego zbioru składającego się ze wszystkich przegród zbioru n na k (ewentualnie pustych) rozróżnialnych pól, A ₁ , A ₂ , ..., A _k , oraz właściwości P _i oznaczających, że przegroda ma pole A _i puste, zasada włączenia-wykluczenia daje odpowiedź na powiązany wynik. Dzielenie przez k ! aby usunąć sztuczne uporządkowanie podaje się liczbę Stirlinga drugiego rodzaju:

${\ Displaystyle S (n, k) = {\ Frac {1} {k!}} \ suma _ {t = 0} ^ {k} (-1) ^ {t} {\ binom {k} {t} }(kt)^{n}.}$

Wielomiany wieżowe

Wielomian wież jest funkcją generującą liczbę sposobów umieszczenia wież nieatakujących na planszy B, która wygląda jak podzbiór kwadratów szachownicy ; oznacza to, że żadne dwie wieże nie mogą znajdować się w tym samym rzędzie lub kolumnie. Plansza B jest dowolnym podzbiorem kwadratów prostokątnej planszy zn rzędami i m kolumnami; myślimy o tym jako o polach, w które można postawić wieżę. Współczynnik , R _K ( B ) o x ^k w wieżę wielomianu R _B ( x ) jest szereg sposobów k wież, z których żadna nie atakuje siebie, mogą być ustawione na placach B . Dla każdej planszy B istnieje plansza uzupełniająca składająca się z kwadratów planszy prostokątnej, których nie ma w B . Ta komplementarna plansza ma również wielomian wieżowy ze współczynnikami${\displaystyle B'}$${\ Displaystyle R_ {B'} (x)}$${\ Displaystyle r_ {k} (B').}$

Czasami wygodnie jest móc obliczyć najwyższy współczynnik wielomianu wieży w kategoriach współczynników wielomianu wieży tablicy komplementarnej. Bez utraty ogólności możemy założyć, że n ≤ m , więc współczynnik ten wynosi r _n ( B ). Liczbę sposobów umieszczenia n nieatakujących wież na całej „szachownicy” n × m (bez względu na to, czy wieże są umieszczone w polach szachownicy B ) jest określona przez silnię opadającą :

${\ Displaystyle (m) _ {n} = m (m-1) (m-2) \ cdots (m-n + 1).}$

Niech P _i będzie własnością, że przypisanie n nieatakujących wież na całej szachownicy ma w kolumnie i wieżę, która nie znajduje się w kwadracie szachownicy B , to zgodnie z zasadą włączenia-wykluczenia mamy:

${\ Displaystyle r_ {n} (B) = \ suma _ {t = 0} ^ {n} (-1) ^ {t} (mt) _ {nt} r_ {t} (B ').}$

Funkcja phi Eulera

Totient Eulera lub funkcja phi, φ ( n ) jest funkcją arytmetyczną, która zlicza liczbę dodatnich liczb całkowitych mniejszych lub równych n, które są względnie pierwsze do n . Oznacza to, że jeśli n jest dodatnią liczbą całkowitą , to φ( n ) jest liczbą liczb całkowitych k z zakresu 1 ≤ k ≤ n, które nie mają wspólnego czynnika z n innym niż 1. Zasada włączenia-wykluczenia służy do uzyskania wzór na φ( n ). Niech S być zestawu {1, ..., n }, a określenie własność P _ja się, że numer w S jest podzielna przez liczby pierwsze p _ı , 1 ≤ i ≤ R , gdzie czynniki pierwsze z

${\ Displaystyle n = p_ {1} ^ {a_ {1}} p_ {2} ^ {a_ {2}} \ cdots p_ {r} ^ {a_ {r}}.}$

Następnie,

${\ Displaystyle \ varphi (n) = n - \ suma _ {i = 1} ^ {r} {\ Frac {n} {p_ {i}}} + \ suma _ {1 \ leqslant ja <j \ leqslant r }{\frac {n}{p_{i}p_{j}}}-\cdots =n\prod _{i=1}^{r}\left(1-{\frac {1}{p_{i }}}\Prawidłowy).}$

Rozwodniona zasada włączenia-wykluczenia

W wielu przypadkach, w których zasada mogłaby dać dokładną formułę (w szczególności liczenie liczb pierwszych za pomocą sita Eratostenesa ), formuła powstająca nie oferuje użytecznej treści, ponieważ liczba zawartych w niej terminów jest nadmierna. Jeśli każdy termin z osobna można dokładnie oszacować, nagromadzenie błędów może sugerować, że wzór włączenia-wykluczenia nie ma bezpośredniego zastosowania. W teorii liczb problem ten został rozwiązany przez Viggo Bruna . Po powolnym starcie jego pomysły zostały podchwycone przez innych i opracowano wiele różnych metod sitowych . Mogą one na przykład próbować znaleźć górne granice dla „przesianych” zestawów, a nie dokładną formułę.

Niech A ₁ , ..., A _n będą dowolnymi zbiorami i p ₁ , ..., p _n liczbami rzeczywistymi w przedziale domkniętej jednostki [0,1]. Wówczas dla każdej liczby parzystej k w {0,..., n } funkcje wskaźnikowe spełniają nierówność:

${\ Displaystyle 1_ {A_ {1} \ filiżanka \ cdots \ filiżanka A_ {n}} \ geq \ suma _ {j = 1} ^ {k} (-1) ^ {j-1} \ suma _ {1 \ leq i_{1}<\cdots <i_{j}\leq n}p_{i_{1}}\dots p_{i_{j}}\,1_{A_{i_{1}}\cap \cdots \cap A_{i_{j}}}.}$

Dowód głównego oświadczenia

Wybierz element zawarty w unii wszystkich zestawów i niech będą poszczególne zestawy, które go zawierają. (Zauważ, że t > 0.) Ponieważ element jest liczony dokładnie raz po lewej stronie równania ( 1 ), musimy pokazać, że jest liczony dokładnie raz po prawej stronie. Po prawej stronie jedyne niezerowe wkłady występują, gdy wszystkie podzbiory w określonym terminie zawierają wybrany element, czyli wszystkie podzbiory są wybrane z . Wkład wynosi jeden dla każdego z tych zestawów (plus lub minus w zależności od terminu), a zatem jest to tylko (podpisana) liczba tych podzbiorów używanych w terminie. Mamy wtedy: ${\displaystyle A_{1},A_{2},\kropki,A_{t}}$${\displaystyle A_{1},A_{2},\kropki,A_{t}}$

${\ Displaystyle {\ zacząć {wyrównany} | \ {A_ {i} \ mid 1 \ leqslant ja \ leqslant t \} | i - | \ {A_ {i} \ cap A_ {j} \ mid 1 \ leqslant i < j\leqslant t\}|+\cdots +(-1)^{t+1}|\{A_{1}\cap A_{2}\cap \cdots \cap A_{t}\}|={\ binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}}.\end{wyrównany}} }$

Przez twierdzenie dwumianowe ,

${\ Displaystyle 0 = (1-1) ^ {t} = {\ binom {t} {0}} - {\ binom {t} {1}} + {\ binom {t} {2}} - \ cdots +(-1)^{t}{\binom {t}{t}}.}$

Korzystając z tego i zmieniając terminy, mamy ${\displaystyle {\binom {t}{0}}=1}$

${\ Displaystyle 1 = {\ binom {t} {1}} - {\ binom {t} {2}} + \ cdots + (-1) ^ {t + 1} {\ binom {t} t}} ,}$

i tak wybrany element jest liczony tylko raz po prawej stronie równania ( 1 ).

Dowód algebraiczny

Dowód algebraiczny można uzyskać za pomocą funkcji wskaźnikowych (znanych również jako funkcje charakterystyczne). Funkcją wskaźnikową podzbioru S zbioru X jest funkcja

${\ Displaystyle {\ zacząć {przypadki} \ mathbf {1} _ {S}: X \ {0, 1 \} \ \ \ mathbf {1} _ {S} (x) = {\ zacząć {przypadki} 1&x\w S\\0&x\now S\end{przypadkach}}\end{przypadkach}}}$

Jeśli i są dwoma podzbiorami , to ${\ Displaystyle A}$${\ Displaystyle B}$${\ Displaystyle X}$

${\ Displaystyle \ mathbf {1} _ {A} \ cdot \ mathbf {1} _ {B} = \ mathbf {1} _ {A \ czapka B}.}$

Niech A oznacza sumę zbiorów A ₁ , ..., A _n . Aby ogólnie udowodnić zasadę włączenia-wykluczenia, najpierw weryfikujemy tożsamość ${\textstyle \bigcup _{i=1}^{n}A_{i}}$

${\ Displaystyle \ mathbf {1} _ {A} = \ suma _ {k = 1} ^ {n} (-1) ^ {k-1} \ suma _ {I \ podzbiór \ {1, \ ldots, n \} \atop |I|=k}\mathbf {1} _{A_{I}}}$

(∗)

dla funkcji wskaźników, gdzie:

${\ Displaystyle A_ {I} = \ bigcap _ {i \ w I} A_ {i}}.$

Następująca funkcja

${\ Displaystyle \ lewo (\ mathbf {1} _ {A} - \ mathbf {1} _ {A_ {1}} \ po prawej) \ lewo (\ mathbf {1} _ {A} - \ mathbf {1} _ {A_{2}}\right)\cdots \left(\mathbf {1} _{A}-\mathbf {1} _{A_{n}}\right),}$

jest identycznie zero, ponieważ: jeśli x nie jest w A , to wszystkie czynniki wynoszą 0 − 0 = 0; w przeciwnym razie, jeśli x należy do jakiegoś A _m , to odpowiadający mu m- ^ty czynnik wynosi 1 − 1 = 0. Rozwijając iloczyn po lewej stronie, następuje równanie (∗).

Aby udowodnić zasadę inkluzji-wykluczenia dla liczności zbiorów, zsumuj równanie (∗) po wszystkich x w związku A ₁ , ..., A _n . Aby wyprowadzić wersję używaną z prawdopodobieństwem, weź oczekiwanie w (∗). Ogólnie całkujemy równanie (∗) względem  μ . Zawsze używaj liniowości w tych wyprowadzeniach.

Zobacz też

• Zasady kombinatoryczne
• Nierówność Boole'a
• Problem z naszyjnikiem
• Wzór Schuette-Nesbitta
• Tożsamość maksimum-minimum

Uwagi

Bibliografia

• Allenby, RBJT; Slomson, Alan (2010), Jak liczyć: Wprowadzenie do kombinatoryki , Matematyka dyskretna i jej zastosowania (2 wyd.), CRC Press, s. 51-60, ISBN 9781420082609
• Björklund, A.; Husfeldt, T.; Koivisto, M. (2009), "Ustaw partycjonowanie przez włączenie-wykluczenie", SIAM Journal on Computing , 39 (2): 546-563, doi : 10.1137/070683933
• Brualdi, Richard A. (2010), Wstępna kombinatoryka (5th ed.), Prentice-Hall, ISBN 9780136020400
• Cameron, Peter J. (1994), Kombinatoryka: tematy, techniki, algorytmy , Cambridge University Press, ISBN 0-521-45761-0
• Fernández, Roberto; Fröhlich, Jürg ; Alan D., Sokal (1992), Random Walks, Critical Phenomena and Triviaity in Quantum Field Theory , Texts an Monographs in Physics, Berlin: Springer-Verlag , s. xviii+444, ISBN 3-540-54358-9, MR  1219313 , Zbl  0761.60061
• Graham, RL; Grötschel, M .; Lovász, L. (1995), Hand Book of Combinatorics (tom 2) , MIT Press – Holandia Północna, ISBN 9780262071710
• Gross, Jonathan L. (2008), Metody kombinatoryczne z aplikacjami komputerowymi , Chapman&Hall/CRC, ISBN 9781584887430
• „Zasada włączenia i wykluczenia” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• Mazur, David R. (2010), Combinatorics A Guided Tour , The Mathematical Association of America, ISBN 9780883857625
• Roberts, Fred S.; Tesman, Barry (2009), kombinatoryka stosowana (2nd ed.), CRC Press, ISBN 9781420099829
• Stanley, Richard P. (1986), Enumerative Combinatorics Tom I , Wadsworth & Brooks / Cole, ISBN 0534065465
• van Linta, JH; Wilson, RM (1992), Kurs kombinatoryki , Cambridge University Press, ISBN 0521422604

Ten artykuł zawiera materiał z zasady włączenia-wykluczenia w PlanetMath , który jest objęty licencją Creative Commons Attribution/Share-Alike License .