Metoda Eulera - Euler method

Równania różniczkowe
Równania różniczkowe Naviera-Stokesa stosowane do symulacji przepływu powietrza wokół przeszkody
Zakres Nauki przyrodnicze Inżynieria Astronomia Fizyka Chemia Biologia Geologia Matematyka stosowana Mechanika kontinuum Teoria chaosu Układy dynamiczne Nauki społeczne Ekonomia Dynamika populacji
Klasyfikacja
Rodzaje Zwykły Częściowy Różniczkowo-algebraiczny Całko-różnicowy Frakcyjny Liniowy Nieliniowy Według typu zmiennej Zmienne zależne i niezależne Autonomiczny Złożony Połączone / Oddzielone Dokładny Jednorodne  / Niejednorodne Cechy Zamówienie Operator Notacja
Związek z procesami Różnica (dyskretny analog) Stochastyczny Stochastyczne częściowe Opóźnienie
Rozwiązanie
Istnienie i wyjątkowość Twierdzenie Picarda-Lindelöfa Twierdzenie o istnieniu Peano Twierdzenie o istnieniu Carathéodory'ego Twierdzenie Cauchy'ego-Kowalewskiego
Tematy ogólne wroński Portret fazowy Przestrzeń fazowa Lapunow  / Asymptotyczna  / Stabilność wykładnicza Wskaźnik konwergencji Seria  / Rozwiązania integralne Całkowanie numeryczne Funkcja delta Diraca
Metody rozwiązania Kontrola Metoda charakterystyki Euler Wykładnicza formuła odpowiedzi Różnica skończona  ( Crank-Nicolson ) Końcowy element Nieskończony element Skończona objętość Galerkin Pietrow-Galerkin Czynnik integrujący Przekształcenia całkowe Teoria zaburzeń Runge-Kutta Separacja zmiennych Nieokreślone współczynniki Zmienność parametrów
Ludzie Izaak Newton Gottfrieda Leibniza Leonhard Euler Emil Picard Józef Maria Hoene-Wroński Ernst Lindelöf Rudolf Lipschitz Augustin-Louis Cauchy John Crank Phyllis Nicolson Carl David Tolmé Runge Martin Kutta
v T mi

Ilustracja metody Eulera. Nieznana krzywa jest na niebiesko, a jej przybliżenie wielokątne na czerwono.

W matematyce oraz informatyce The metodę Eulera (zwany również przodu metodą Eulera ) jest pierwszego rzędu liczbowa procedury rozwiązania równań różniczkowych (Ody) z określoną wartością początkową . Jest to najbardziej podstawowy wyraźny sposób do numerycznego całkowania równań różniczkowych zwyczajnych i to najprostsza metoda Runge-Kutty . Metoda Eulera nosi imię Leonharda Eulera , który potraktował ją w swojej książce Institutionum calculi integralis (wyd. 1768–1870).

Metoda Eulera jest metodą pierwszego rzędu, co oznacza, że ​​błąd lokalny (błąd na krok) jest proporcjonalny do kwadratu wielkości kroku, a błąd globalny (błąd w danym czasie) jest proporcjonalny do wielkości kroku. Metoda Eulera często służy jako podstawa do konstruowania bardziej złożonych metod, np. metody predyktor-korektor .

Nieformalny opis geometryczny

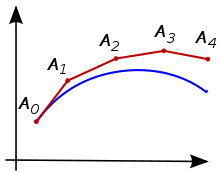
Rozważ problem obliczenia kształtu nieznanej krzywej, która zaczyna się w danym punkcie i spełnia dane równanie różniczkowe. W tym przypadku równanie różniczkowe może być traktowany jako wzór w którym nachylenie w linii stycznej do krzywej można obliczyć w dowolnym punkcie na krzywej, gdy została obliczona położenie tego punktu.

Chodzi o to, że chociaż krzywa jest początkowo nieznana, jej punkt początkowy, który oznaczamy, jest znany (patrz rysunek w prawym górnym rogu). Następnie z równania różniczkowego można obliczyć nachylenie do krzywej w , a więc linię styczną. ${\displaystyle A_{0},}$${\displaystyle A_{0}}$

Zrób mały krok wzdłuż tej stycznej do punktu Wzdłuż tego małego kroku nachylenie nie zmienia się zbytnio, więc będzie blisko łuku. Jeśli założymy, że nadal jest na krzywej, można zastosować to samo rozumowanie, jak w przypadku powyższego punktu . Po kilku krokach obliczana jest krzywa wielokątna . Ogólnie ta krzywa nie odbiega zbyt daleko od pierwotnej nieznanej krzywej, a błąd między dwiema krzywymi może być mały, jeśli wielkość kroku jest wystarczająco mała, a przedział obliczeń jest skończony: ${\displaystyle A_{1}.}$${\displaystyle A_{1}}$${\displaystyle A_{1}}$${\displaystyle A_{0}}$ ${\displaystyle A_{0}A_{1}A_{2}A_{3}\kropki}$

${\ Displaystyle y'(t)=f(t,y(t)),\qquad r(t_{0})=y_{0}.}$

Wybierz wartość dla rozmiaru każdego kroku i ustaw . Teraz jeden krok metody Eulera od do to: ${\ Displaystyle h}$${\displaystyle t_{n}=t_{0}+nh}$${\displaystyle t_{n}}$${\ Displaystyle t_ {n + 1} = t_ {n} + h}$

${\ Displaystyle y_ {n + 1} = y_ {n} + hf (t_ {n}, y_ {n}).}$

Wartość jest przybliżeniem rozwiązania ODE w czasie : . Metoda Eulera jest jawna , tzn. rozwiązanie jest jawną funkcją for . ${\ Displaystyle y_ {n}}$${\displaystyle t_{n}}$${\ Displaystyle y_ {n} \ w przybliżeniu r (t_ {n})}$${\displaystyle y_{n+1}}$${\displaystyle y_{i}}$${\displaystyle ja\leq n}$

Podczas gdy metoda Eulera integruje ODE pierwszego rzędu, każdy ODE rzędu N może być reprezentowany jako układ ODE pierwszego rzędu: aby traktować równanie

${\ Displaystyle y ^ {(N)} (t) = f (t, y (t), y '(t), \ ldots, y ^ {(N-1)} (t))}$,

wprowadzamy zmienne pomocnicze i otrzymujemy równanie równoważne: ${\ Displaystyle z_ {1} (t) = r (t), z_ {2} (t) = r (t), \ ldots, z_ {N} (t) = y ^ {(N-1)} (T)}$

${\ Displaystyle \ mathbf {z} '(t) = {\ zacznij {pmatrix} z_ {1} '(t) \ \ \ vdots \ \ z_ {N-1} '(t) \ \ z_ {N} ' (t)\end{pmatrix}}={\begin{pmatrix}y'(t)\\\vdots \\y^{(N-1)}(t)\\y^{(N)}(t )\end{pmatrix}}={\begin{pmatrix}z_{2}(t)\\\vdots \\z_{N}(t)\\f(t,z_{1}(t),\ldots ,z_{N}(t))\end{pmacierz}}}$

Jest to system pierwszego rzędu w zmiennej i może być obsługiwany metodą Eulera lub, w rzeczywistości, dowolnym innym schematem dla systemów pierwszego rzędu. ${\ Displaystyle \ mathbf {z} (t)}$

Przykład

Biorąc pod uwagę problem z wartością początkową

${\displaystyle y'=y,\quad y(0)=1,}$

chcielibyśmy użyć metody Eulera do przybliżenia . ${\displaystyle y(4)}$

Stosując rozmiar kroku równy 1 ( h = 1)

Ilustracja całkowania numerycznego dla równania Blue to metoda Eulera; zielony, metoda punktu środkowego ; czerwony, rozwiązanie dokładne, Wielkość kroku to h  = 1,0 .${\displaystyle y'=y,y(0)=1.}$${\ Displaystyle y = e ^ {t}.}$

Metoda Eulera to

${\ Displaystyle y_ {n + 1} = y_ {n} + hf (t_ {n}, y_ {n}). \ qquad \ qquad}$

więc najpierw musimy obliczyć . W tym prostym równaniu różniczkowym funkcja jest zdefiniowana przez . Mamy ${\displaystyle f(t_{0},y_{0})}$${\displaystyle f}$${\displaystyle f(t,y)=y}$

${\displaystyle f(t_{0},y_{0})=f(0,1)=1.\qquad \qquad}$

Wykonując powyższy krok, znaleźliśmy nachylenie prostej stycznej do krzywej rozwiązania w punkcie . Przypomnijmy, że nachylenie jest zdefiniowane jako zmiana podzielona przez zmianę lub . ${\ Displaystyle (0,1)}$${\displaystyle y}$${\displaystyle t}$${\ Displaystyle \ Delta r / \ Delta t}$

Następnym krokiem jest pomnożenie powyższej wartości przez rozmiar kroku , który tutaj przyjmujemy jako jeden: ${\ Displaystyle h}$

${\ Displaystyle h \ cdot f (y_ {0}) = 1 \ cdot 1 = 1. \ qquad \ qquad }$

Ponieważ wielkość kroku to zmiana w , gdy pomnożymy wielkość kroku i nachylenie stycznej, otrzymamy zmianę wartości. Ta wartość jest następnie dodawana do wartości początkowej, aby uzyskać następną wartość do wykorzystania w obliczeniach. ${\displaystyle t}$${\displaystyle y}$${\displaystyle y}$

${\displaystyle y_{0}+hf(y_{0})=y_{1}=1+1\cdot 1=2.\qquad \qquad}$

Powyższe kroki należy powtórzyć, aby znaleźć , i . ${\displaystyle y_{2}}$${\displaystyle Y_{3}}$${\displaystyle y_{4}}$

${\ Displaystyle {\ zacząć {wyrównany} y_ {2} i = y_ {1} + hf (y_ {1}) = 2 + 1 \ cdot 2 = 4 \ \ y_ {3}& = y_ {2} + hf(y_{2})=4+1\cdot 4=8,\\y_{4}&=y_{3}+hf(y_{3})=8+1\cdot 8=16.\end{ wyrównany}}}$

Ze względu na powtarzalny charakter tego algorytmu pomocne może być zorganizowanie obliczeń w formie wykresu, jak pokazano poniżej, aby uniknąć błędów.

${\ Displaystyle n}$	${\ Displaystyle y_ {n}}$	${\displaystyle t_{n}}$	${\ Displaystyle f (t_ {n}, y_ {n})}$	${\ Displaystyle h}$	${\ Displaystyle \ Delta y}$	${\displaystyle y_{n+1}}$
0	1	0	1	1	1	2
1	2	1	2	1	2	4
2	4	2	4	1	4	8
3	8	3	8	1	8	16

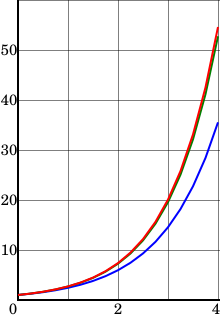
Wniosek z tego obliczenia jest taki, że . Dokładnym rozwiązaniem równania różniczkowego jest , więc . Chociaż aproksymacja metody Eulera w tym konkretnym przypadku nie była zbyt dokładna, szczególnie ze względu na duży rozmiar kroku wartości , jej zachowanie jest jakościowo poprawne, jak pokazuje rysunek. ${\ Displaystyle y_{4}=16}$${\ Displaystyle y (t) = e ^ {t}}$${\ Displaystyle y (4) = e ^ {4} \ około 54,598}$${\ Displaystyle h}$

Przykład kodu MATLAB

clear; clc; close('all');
y0 = 1;
t0 = 0;
h = 1; % try: h = 0.01
tn = 4; % equal to: t0 + h*n, with n the number of steps
[t, y] = Euler(t0, y0, h, tn);
plot(t, y, 'b');

% exact solution (y = e^t):
tt = (t0:0.001:tn);
yy = exp(tt);
hold('on');
plot(tt, yy, 'r');
hold('off');
legend('Euler', 'Exact');

function [t, y] = Euler(t0, y0, h, tn)
    fprintf('%10s%10s%10s%15s\n', 'i', 'yi', 'ti', 'f(yi,ti)');
    fprintf('%10d%+10.2f%+10.2f%+15.2f\n', 0, y0, t0, f(y0, t0));
    t = (t0:h:tn)';
    y = zeros(size(t));
    y(1) = y0;
    for i = 1:1:length(t) - 1
        y(i + 1) = y(i) + h * f(y(i), t(i));
        fprintf('%10d%+10.2f%+10.2f%+15.2f\n', i, y(i + 1), t(i + 1), f(y(i + 1), t(i + 1)));
    end
end

% in this case, f(y,t) = f(y)
function dydt = f(y, t)
    dydt = y;
end

% OUTPUT:
%         i        yi        ti       f(yi,ti)
%         0     +1.00     +0.00          +1.00
%         1     +2.00     +1.00          +2.00
%         2     +4.00     +2.00          +4.00
%         3     +8.00     +3.00          +8.00
%         4    +16.00     +4.00         +16.00
% NOTE: Code also outputs a comparison plot

Przykład kodu R

Graficzne wyjście kodu języka programowania R dla przedstawionego przykładu

Poniżej znajduje się kod na przykład w języku programowania R .

# ============
# SOLUTION to
#   y' = y,   where y' = f(t,y)
# then:
f <- function(ti,y) y

# INITIAL VALUES:
t0 <- 0
y0 <- 1
h  <- 1
tn <- 4

# Euler's method: function definition
Euler <- function(t0, y0, h, tn, dy.dt) {
  # dy.dt: derivative function
  
  # t sequence:
  tt <- seq(t0, tn, by=h)
  # table with as many rows as tt elements:
  tbl <- data.frame(ti=tt)
  tbl$yi <- y0 # Initializes yi with y0
  tbl$Dy.dt[1] <- dy.dt(tbl$ti[1],y0) # derivative
  for (i in 2:nrow(tbl)) {
    tbl$yi[i] <- tbl$yi[i-1] + h*tbl$Dy.dt[i-1]
    # For next iteration:
    tbl$Dy.dt[i] <- dy.dt(tbl$ti[i],tbl$yi[i])
  }
  return(tbl)
}

# Euler's method: function application
r <- Euler(t0, y0, h, tn, f)
rownames(r) <- 0:(nrow(r)-1) # to coincide with index n

# Exact solution for this case: y = exp(t)
#       added as an additional column to r
r$y <- exp(r$ti)

# TABLE with results:
print(r)

plot(r$ti, r$y, type="l", col="red", lwd=2)
lines(r$ti, r$yi, col="blue", lwd=2)
grid(col="black")
legend("top",  legend = c("Exact", "Euler"), lwd=2,  col = c("red", "blue"))

# OUTPUT:
#
#   ti yi Dy.dt         y
# 0  0  1     1  1.000000
# 1  1  2     2  2.718282
# 2  2  4     4  7.389056
# 3  3  8     8 20.085537
# 4  4 16    16 54.598150
# NOTE: Code also outputs a comparison plot

Korzystanie z innych rozmiarów kroku

Ta sama ilustracja dla h  = 0,25.

Jak zasugerowano we wstępie, metoda Eulera jest dokładniejsza, jeśli wielkość kroku jest mniejsza. Poniższa tabela pokazuje wynik z różnymi rozmiarami stopni. Górny rząd odpowiada przykładowi z poprzedniej sekcji, a drugi rząd jest przedstawiony na rysunku. ${\ Displaystyle h}$

Rozmiar kroku	wynik metody Eulera	błąd
1	16.00	38,60
0,25	35,53	19.07
0,1	45,26	9.34
0,05	49,56	5.04
0,025	51,98	2,62
0,0125	53,26	1.34

Błąd odnotowany w ostatniej kolumnie tabeli to różnica między dokładnym rozwiązaniem w a przybliżeniem Eulera. Na dole tabeli rozmiar kroku to połowa rozmiaru kroku w poprzednim wierszu, a błąd jest również w przybliżeniu połową błędu w poprzednim wierszu. Sugeruje to, że błąd jest w przybliżeniu proporcjonalny do wielkości kroku, przynajmniej dla dość małych wartości wielkości kroku. Generalnie dotyczy to również innych równań; zobacz sekcję Globalny błąd obcinania, aby uzyskać więcej informacji. ${\displaystyle t=4}$

Inne metody, takie jak metoda punktu środkowego również pokazana na rysunkach, zachowują się korzystniej: błąd globalny metody punktu środkowego jest w przybliżeniu proporcjonalny do kwadratu wielkości kroku. Z tego powodu mówi się, że metoda Eulera jest metodą pierwszego rzędu, podczas gdy metoda punktu środkowego jest metodą drugiego rzędu.

Możemy ekstrapolować z powyższej tabeli, że rozmiar kroku potrzebny do uzyskania odpowiedzi poprawnej do trzech miejsc po przecinku wynosi około 0,00001, co oznacza, że ​​potrzebujemy 400 000 kroków. Ta duża liczba kroków pociąga za sobą wysokie koszty obliczeniowe. Z tego powodu stosuje się metody wyższego rzędu, takie jak metody Runge-Kutta lub liniowe metody wieloetapowe , zwłaszcza jeśli pożądana jest wysoka dokładność.

Pochodzenie

Metodę Eulera można wyprowadzić na wiele sposobów. Po pierwsze, powyżej znajduje się opis geometryczny.

Inną możliwością jest rozważenie rozwinięcia Taylora funkcji wokół : ${\displaystyle y}$${\displaystyle t_{0}}$

${\ Displaystyle y (t_ {0}+ h) = r (t_ {0}) + hy '(t_ {0}) + {\ Frac {1} {2}} h ^ {2} r '' (t_ {0})+O(h^{3}).}$

Równanie różniczkowe stwierdza, że . Jeśli zostanie to podstawione w rozwinięciu Taylora, a człony kwadratowe i wyższego rzędu są ignorowane, powstaje metoda Eulera. Rozszerzenie Taylora jest używane poniżej do analizy błędu popełnionego przez metodę Eulera i może być rozszerzone na tworzenie metod Runge-Kutty . ${\displaystyle y'=f(t,y)}$

Ściśle pokrewnym wyprowadzeniem jest zastąpienie pochodnej wzoru różnic skończonych w przód ,

${\ Displaystyle y '(t_ {0}) \ około {\ Frac {y (t_ {0}+ h)-y (t_ {0})} {h}}}$

w równaniu różniczkowym . Ponownie daje to metodę Eulera. Podobne obliczenia prowadzą do metody punktu środkowego i wstecznej metody Eulera . ${\displaystyle y'=f(t,y)}$

Na koniec można scałkować równanie różniczkowe od do i zastosować podstawowe twierdzenie rachunku różniczkowego, aby uzyskać: ${\displaystyle t_{0}}$${\displaystyle t_{0}+h}$

${\ Displaystyle y (t_ {0}+ h)-y (t_ {0}) = \ int _ {t_ {0}} ^ {t_ {0}+ h} f (t, r (t)) \, \mathrm {d} t.}$

Teraz przybliż całkę metodą prostokąta po lewej stronie (z tylko jednym prostokątem):

${\ Displaystyle \ int _ {t_ {0}} ^ {t_ {0}+ h} f (t, y (t)) \, \ operatorname {d} t \ około hf (t_ {0}, y (t_) {0})).}$

Łącząc oba równania, ponownie znajdujemy metodę Eulera. Ten tok myślenia można kontynuować, aby dojść do różnych liniowych, wieloetapowych metod .

Błąd lokalnego obcinania

Lokalny błąd obcięcia metody Eulera jest błąd popełniony w jednym kroku. Jest to różnica między rozwiązaniem numerycznym po jednym kroku , a dokładnym rozwiązaniem w czasie . Rozwiązanie numeryczne jest podane przez ${\displaystyle Y_{1}}$${\displaystyle t_{1}=t_{0}+h}$

${\displaystyle y_{1}=y_{0}+hf(t_{0},y_{0}).\quad}$

Dla dokładnego rozwiązania używamy rozwinięcia Taylora wspomnianego w sekcji Wyprowadzenie powyżej:

${\ Displaystyle y (t_ {0}+ h) = r (t_ {0}) + hy '(t_ {0}) + {\ Frac {1} {2}} h ^ {2} r '' (t_ {0})+O(h^{3}).}$

Lokalny błąd obcięcia (LTE) wprowadzony metodą Eulera wynika z różnicy między tymi równaniami:

${\ Displaystyle \ operatorname {LTE} = r (t_ {0}+ h)-y_ {1} = {\ Frac {1} {2}} h ^ {2} r ''(t_ {0}) + O (h^{3}).}$

Ten wynik jest ważny, jeśli ma ograniczoną trzecią pochodną. ${\displaystyle y}$

To pokazuje, że dla small , lokalny błąd obcięcia jest w przybliżeniu proporcjonalny do . To sprawia, że ​​metoda Eulera jest mniej dokładna (dla małych ) niż inne techniki wyższego rzędu, takie jak metody Runge-Kutta i liniowe metody wieloetapowe , dla których lokalny błąd obcięcia jest proporcjonalny do większej mocy wielkości kroku. ${\ Displaystyle h}$${\ Displaystyle h ^ {2}}$${\ Displaystyle h}$

Nieco inne sformułowanie dla lokalnego błędu obcięcia można uzyskać, używając formy Lagrange'a dla pozostałego członu w twierdzeniu Taylora . Jeżeli ma ciągłą drugą pochodną, ​​to istnieje taka, że ${\displaystyle y}$${\ Displaystyle \ xi \ w [t_{0},t_{0}+h]}$

${\ Displaystyle \ operatorname {LTE} = r (t_ {0}+ h)-y_ {1} = {\ Frac {1} {2}} h ^ {2} r ''(\ XI).}$

W powyższych wyrażeniach na błąd drugą pochodną nieznanego rozwiązania dokładnego można zastąpić wyrażeniem obejmującym prawą stronę równania różniczkowego. Rzeczywiście, z równania wynika, że ${\displaystyle y}$${\displaystyle y'=f(t,y)}$

${\ Displaystyle y ''(t_ {0}) = {\ częściowy f \ nad \ częściowy t} (t_ {0}, y (t_ {0})) + {\ częściowy f \ nad \ częściowy y} (t_ {0},y(t_{0}))\,f(t_{0},y(t_{0})).}$

Globalny błąd obcinania

Globalny błąd obcięcia jest błąd w ustalonym czasie , jednak po wielu kroków metody powinna podjąć, aby osiągnąć ten czas od momentu początkowego. Globalny błąd obcinania jest skumulowanym efektem lokalnych błędów obcinania popełnionych na każdym kroku. Liczba kroków jest łatwo określona jako , która jest proporcjonalna do , a błąd popełniony w każdym kroku jest proporcjonalny do (patrz poprzedni rozdział). Dlatego należy oczekiwać, że globalny błąd obcięcia będzie proporcjonalny do . ${\displaystyle t}$${\ Displaystyle (t-t_ {0})/h}$${\ Displaystyle 1/h}$${\ Displaystyle h ^ {2}}$${\ Displaystyle h}$

To intuicyjne rozumowanie można sprecyzować. Jeżeli rozwiązanie ma ograniczoną drugą pochodną i jest w drugim argumencie ciągiem Lipschitza , to globalny błąd obcięcia (GTE) jest ograniczony przez ${\displaystyle y}$${\displaystyle f}$

${\ Displaystyle | {\ tekst {GTE}} | \ leq {\ Frac {hM} {2L}} (e ^ {L (t-t_ {0})} -1) \ qquad \ qquad}$

gdzie jest górnym ograniczeniem drugiej pochodnej na danym przedziale i jest stałą Lipschitza . ${\ Displaystyle M}$${\displaystyle y}$${\ Displaystyle L}$${\displaystyle f}$

Dokładna forma tego wiązania ma niewielkie znaczenie praktyczne, ponieważ w większości przypadków wiązanie to znacznie przecenia rzeczywisty błąd popełniony przez metodę Eulera. Co ważne, pokazuje, że globalny błąd obcięcia jest (w przybliżeniu) proporcjonalny do . Z tego powodu mówi się, że metoda Eulera jest metodą pierwszego rzędu. ${\ Displaystyle h}$

Stabilność numeryczna

Rozwiązanie obliczone metodą Eulera z wielkością kroku (niebieskie kwadraty) i (czerwone kółka). Czarna krzywa pokazuje dokładne rozwiązanie.${\displaystyle y'=-2,3y}$${\displaystyle h=1}$${\ Displaystyle h = 0,7}$

Metoda Eulera może być również numerycznie niestabilna , zwłaszcza dla sztywnych równań , co oznacza, że ​​rozwiązanie numeryczne staje się bardzo duże dla równań, w których rozwiązanie dokładne nie. Można to zilustrować za pomocą równania liniowego

${\ Displaystyle y' = -2,3 y \ qquad y (0) = 1.}$

Dokładnym rozwiązaniem jest , które rozpada się do zera jako . Jeśli jednak zastosujemy metodę Eulera do tego równania z rozmiarem kroku , to rozwiązanie numeryczne jest jakościowo błędne: oscyluje i rośnie (patrz rysunek). To właśnie oznacza być niestabilnym. Jeśli na przykład zostanie użyty mniejszy krok , to rozwiązanie numeryczne rozpada się do zera. ${\ Displaystyle y (t) = e ^ {-2,3 t}}$${\displaystyle t\do \infty}$${\displaystyle h=1}$${\ Displaystyle h = 0,7}$

Różowy krążek pokazuje region stabilności dla metody Eulera.

Jeżeli metoda Eulera zostanie zastosowana do równania liniowego , to rozwiązanie numeryczne jest niestabilne, jeśli iloczyn znajduje się poza regionem ${\displaystyle y'=ky}$${\displaystyle hk}$

${\ Displaystyle \ {z \ w \ mathbf {C} \ mid | z + 1 | \ leq 1 \}}$

zilustrowany po prawej stronie. Region ten nazywany jest (liniowym) regionem stabilności . W przykładzie wynosi −2,3, więc jeśli to jest poza obszarem stabilności, a zatem rozwiązanie numeryczne jest niestabilne. ${\displaystyle k}$${\displaystyle h=1}$${\ Displaystyle hk = -2,3}$

To ograniczenie — wraz z jego powolną zbieżnością błędu z h — oznacza, że ​​metoda Eulera nie jest często używana, z wyjątkiem prostego przykładu całkowania numerycznego.

Błędy zaokrąglania

W dotychczasowej dyskusji pomijano konsekwencje błędu zaokrąglania . W kroku n metody Eulera błąd zaokrąglenia jest w przybliżeniu wielkości ε y _n, gdzie ε jest epsilonem maszyny . Zakładając, że wszystkie błędy zaokrągleń są w przybliżeniu tej samej wielkości, łączny błąd zaokrąglenia w N krokach wynosi w przybliżeniu N ε y _0, jeśli wszystkie błędy wskazują ten sam kierunek. Ponieważ liczba kroków jest odwrotnie proporcjonalna do wielkości kroku h , całkowity błąd zaokrąglenia jest proporcjonalny do ε / h . W rzeczywistości jednak jest bardzo mało prawdopodobne, aby wszystkie błędy zaokrąglania wskazywały ten sam kierunek. Jeżeli zamiast tego założymy, że błędy zaokrągleń są niezależnymi zmiennymi losowymi, to oczekiwany całkowity błąd zaokrąglenia jest proporcjonalny do . ${\ Displaystyle \ varepsilon / {\ sqrt {h}}}$

Tak więc, dla bardzo małych wartości wielkości kroku, błąd obcięcia będzie mały, ale efekt błędu zaokrąglenia może być duży. Większości efektu błędu zaokrąglenia można łatwo uniknąć, jeśli we wzorze na metodę Eulera stosuje się sumowanie skompensowane .

Modyfikacje i rozszerzenia

Prostą modyfikacją metody Eulera, która eliminuje problemy ze stabilnością odnotowane w poprzednim rozdziale, jest wsteczna metoda Eulera :

${\ Displaystyle y_ {n + 1} = y_ {n} + hf (t_ {n + 1}, y_ {n + 1}).}$

Różni się to od (standardowej lub wyprzedzającej) metody Eulera tym, że funkcja jest oceniana w punkcie końcowym kroku, a nie w punkcie początkowym. Metoda wstecznego Eulera jest metodą niejawną , co oznacza, że ​​wzór na metodę wstecznego Eulera ma obie strony, więc stosując metodę wstecznego Eulera musimy rozwiązać równanie. To sprawia, że ​​wdrożenie jest bardziej kosztowne. ${\displaystyle f}$${\displaystyle y_{n+1}}$

Inne modyfikacje metody Eulera, które pomagają w utrzymaniu stabilności, dają wykładniczą metodę Eulera lub półukrytą metodę Eulera .

Bardziej skomplikowane metody mogą osiągnąć wyższy rząd (i większą dokładność). Jedną z możliwości jest użycie większej liczby ewaluacji funkcji. Ilustruje to wspomniana już w tym artykule metoda punktu środkowego :

${\ Displaystyle y_ {n + 1} = y_ {n} + hf {\ duży (} t_ {n} + {\ tfrac {1} {2}} h, y_ {n} + {\ tfrac {1} { 2}}hf(t_{n},y_{n}){\Duży )}}$.

Prowadzi to do rodziny metod Runge-Kutty .

Inną możliwością jest użycie większej liczby przeszłych wartości, co ilustruje dwuetapowa metoda Adamsa-Bashfortha:

${\ Displaystyle y_ {n + 1} = y_ {n} + {\ tfrac {3} {2}} hf (t_ {n}, y_ {n}) - {\ tfrac {1} {2}} hf ( t_{n-1},y_{n-1}).}$

Prowadzi to do rodziny liniowych metod wieloetapowych . Istnieją inne modyfikacje, które wykorzystują techniki wykrywania kompresji, aby zminimalizować zużycie pamięci

W kulturze popularnej

W filmie Ukryte figur , Katherine Goble ucieka z metodą Eulera w obliczaniu ponowne wejście astronauta John Glenn z orbity Ziemi.

Zobacz też

• Metoda korby-Nicolsona
• Opadanie gradientowe podobnie wykorzystuje skończone kroki, tutaj, aby znaleźć minima funkcji
• Lista metod Runge-Kutta
• Liniowa metoda wieloetapowa
• Całkowanie numeryczne (do obliczania całek oznaczonych)
• Metody numeryczne dla równań różniczkowych zwyczajnych

Uwagi

Bibliografia

• Atkinson, Kendall A. (1989). Wprowadzenie do analizy numerycznej (wyd. 2). Nowy Jork: John Wiley i Synowie . Numer ISBN 978-0-471-50023-0.
• Ascher, Uri M.; Petzold, Linda R. (1998). Metody komputerowe równań różniczkowych zwyczajnych i równań różniczkowo-algebraicznych . Filadelfia: Towarzystwo Matematyki Przemysłowej i Stosowanej . Numer ISBN 978-0-89871-412-8.
• Rzeźnik, John C. (2003). Metody numeryczne równań różniczkowych zwyczajnych . Nowy Jork: John Wiley i Synowie . Numer ISBN 978-0-471-96758-3.
• Fryzjer, Ernst; Norsett, Syvert Paul; Wanner, Gerhard (1993). Rozwiązywanie równań różniczkowych zwyczajnych I: Problemy niesztywne . Berlin, Nowy Jork: Springer-Verlag . Numer ISBN 978-3-540-56670-0.
• Iserles, Arieh (1996). Pierwszy kurs numerycznej analizy równań różniczkowych . Wydawnictwo Uniwersytetu Cambridge . Numer ISBN 978-0-521-55655-2.
• Stoer, Josef; Bulirsch, Roland (2002). Wprowadzenie do analizy numerycznej (3rd ed.). Berlin, Nowy Jork: Springer-Verlag . Numer ISBN 978-0-387-95452-3.
• Lakoba, Taras I. (2012), Prosta metoda Eulera i jej modyfikacje (PDF) (Lecture notes for MATH334), University of Vermont , pobrane 29 lutego 2012
• Unni, MP (2017). „Redukcja pamięci dla numerycznego rozwiązania równań różniczkowych z wykorzystaniem wykrywania ściskającego”. 2017 IEEE 13th International Colloquium on Signal Processing & its Applications (CSPA) . IEEE CSPA . s. 79–84. doi : 10.1109/CSPA.2017.8064928 . Numer ISBN 978-1-5090-1184-1. S2CID  13082456 .

Zewnętrzne linki

• Multimedia związane z metodą Eulera w Wikimedia Commons
• Implementacje metody Eulera w różnych językach przez Rosetta Code
• „Metoda Eulera” , Encyklopedia Matematyki , EMS Press , 2001 [1994]