Zbiór policzalny - Countable set

W matematyce , A policzalny zestaw jest zestaw z tym samym liczności ( liczba elementów) jako pewien podzbiór zbioru liczb naturalnych . Zbiór przeliczalny jest albo zbiorem skończonym, albo zbiorem przeliczalnie nieskończonym . Niezależnie od tego, czy są skończone, czy nieskończone, elementy zbioru policzalnego zawsze mogą być liczone pojedynczo i — chociaż liczenie może nigdy się nie skończyć — każdy element zbioru jest powiązany z unikalną liczbą naturalną.

Georg Cantor wprowadził pojęcie zbiorów policzalnych, kontrastujących zbiorów policzalnych z niepoliczalnymi . Dzisiaj zbiory policzalne stanowią podstawę gałęzi matematyki zwanej matematyką dyskretną .

Uwaga dotycząca terminologii

Chociaż zdefiniowane tutaj terminy „policzalny” i „przeliczalnie nieskończony” są dość powszechne, terminologia nie jest uniwersalna. Alternatywny styl używa policzalnego, aby oznaczać to, co tutaj nazywamy policzalną nieskończonością, a co najwyżej policzalne, aby oznaczać to, co nazywamy policzalnym. Aby uniknąć dwuznaczności, można ograniczyć się do określeń „co najwyżej policzalny” i „przeliczalnie nieskończony”, choć pod względem zwięzłości jest to najgorsze z obu światów. Czytelnik powinien sprawdzić używaną definicję, gdy napotka w literaturze termin „policzalny”.

Można również używać terminów przeliczalny i przeliczalny , np. w odniesieniu do odpowiednio policzalnej i policzalnej nieskończoności, ale ponieważ definicje się różnią, czytelnikowi zaleca się, aby ponownie sprawdził używaną definicję.

Definicja

Najbardziej zwięzła definicja dotyczy kardynalności . Zbiór $S$ jest policzalny, jeśli jego moc |S| jest mniejsza lub równa ( aleph-null ), moc zbioru liczb naturalnych $N$ . Zbiór $S$ jest przeliczalnie nieskończony, jeśli |S| = . Zbiór jest niepoliczalny, jeśli nie jest policzalny, tj. jego liczność jest większa niż ; Czytelnik jest odsyłany do zestawu Uncountable do dalszej dyskusji. $\aleph_{0}$ $\aleph_{0}$ $\aleph_{0}$

Równoważnie zbiór $S$ jest policzalny iff :

istnieje funkcja iniekcyjna od $S$ do N .
$S$ jest puste lub istnieje funkcja surjektywna od N do $S$ lub .
istnieje bijektywne odwzorowanie między $S$ a podzbiorem N .
$S$ jest albo skończone, albo przeliczalnie nieskończone.

Podobnie zbiór $S$ jest przeliczalnie nieskończony iff :

istnieje odwzorowanie iniektywne i surjektywne (a zatem bijektywne ) między $S$ i N . Innymi słowy, zbiór jest przeliczalnie nieskończony, jeśli odpowiada jeden do jednego ze zbiorem liczb naturalnych $N$ .
Elementy $S$ mogą być ułożone w nieskończonej sekwencji , gdzie różni się od for i każdy element $S$ jest wymieniony. $a_{0},a_{1},a_{2},\ldots$ $a_{i}$ $a_{j}$ $i\neqj$

Historia

W 1874 r. w swoim pierwszym artykule z teorii mnogości Cantor udowodnił, że zbiór liczb rzeczywistych jest niepoliczalny, pokazując tym samym, że nie wszystkie zbiory nieskończone są przeliczalne. W 1878 r. użył korespondencji jeden do jednego, aby określić i porównać kardynałowie. W 1883 roku rozszerzył liczby naturalne o swoje nieskończone liczby porządkowe i użył zbiorów liczb porządkowych do stworzenia nieskończoności zbiorów o różnych nieskończonych mocach.

Wstęp

Zestaw to zbiór elementów i może być opisane na wiele sposobów. Jednym ze sposobów jest po prostu wymienienie wszystkich jego elementów; na przykład zbiór składający się z liczb całkowitych 3, 4 i 5 może być oznaczony jako {3, 4, 5}, zwany formą roster. Jest to jednak skuteczne tylko w przypadku małych zestawów; w przypadku większych zestawów byłoby to czasochłonne i podatne na błędy. Zamiast wymieniać każdy pojedynczy element, czasami używa się wielokropka ("...") do przedstawienia wielu elementów między elementem początkowym a końcowym w zestawie, jeśli autor uważa, że czytelnik może łatwo odgadnąć, co reprezentuje ... ; na przykład {1, 2, 3, ..., 100} prawdopodobnie oznacza zbiór liczb całkowitych od 1 do 100. Nawet w tym przypadku jednak nadal można wymienić wszystkie elementy, ponieważ liczba elementów w zbiór jest skończony.

Niektóre zbiory są nieskończone ; te zestawy mają więcej niż n elementów, gdzie n jest dowolną liczbą całkowitą, którą można określić. (Bez względu na to, jak duża jest określona liczba całkowita n , na przykład n = 9 × 10 ³² , zbiory nieskończone mają więcej niż n elementów.) Na przykład zbiór liczb naturalnych, oznaczany przez {0, 1, 2, 3, 4 , 5, ...} ma nieskończenie wiele elementów i nie możemy użyć żadnej liczby naturalnej do podania jej rozmiaru. Okazuje się jednak, że zbiory nieskończone mają dobrze zdefiniowane pojęcie rozmiaru (a właściwie kardynalność , termin techniczny określający liczbę elementów w zbiorze), a nie wszystkie zbiory nieskończone mają taką samą kardynalność.

Mapowanie bijective od liczb całkowitych do parzystych

Aby zrozumieć, co to oznacza, najpierw zbadajmy, czego to nie znaczy. Na przykład istnieje nieskończenie wiele nieparzystych liczb całkowitych, nieskończenie wiele parzystych liczb całkowitych i (stąd) nieskończenie wiele liczb całkowitych ogółem. Okazuje się jednak, że liczba parzystych liczb całkowitych, która jest równa liczbie nieparzystych liczb całkowitych, jest również taka sama jak liczba całkowitych liczb całkowitych. Dzieje się tak, ponieważ możemy uporządkować rzeczy w taki sposób, że dla każdej liczby całkowitej istnieje odrębna liczba parzysta:

\ldots\,-\!2\!\rightarrow \!-\!4,\,-\!1\!\rightarrow \!-\!2,\,0\!\rightarrow \!0, \,1\!\rightarrow \!2,\,2\!\rightarrow \!4\,\ldots

lub ogólniej (patrz rysunek). To, co zrobiliśmy tutaj, to uporządkowanie liczb całkowitych i parzystych w korespondencję jeden do jednego (lub bijekcję ), która jest funkcją odwzorowującą między dwoma zestawami w taki sposób, że każdy element każdego zestawu odpowiada jednemu elementowi w drugim ustawić.

n\rightarrow 2n

Jednak nie wszystkie zbiory nieskończone mają tę samą kardynalność. Na przykład Georg Cantor (który wprowadził tę koncepcję) wykazał, że liczb rzeczywistych nie można umieścić w korespondencji jeden do jednego z liczbami naturalnymi (nieujemnymi liczbami całkowitymi), a zatem zbiór liczb rzeczywistych ma większą moc niż zbiór liczb naturalnych.

Przegląd formalny

Z definicji zbiór S jest policzalny, jeśli istnieje funkcja iniekcyjna f : S → N od S do liczb naturalnych N = {0, 1, 2, 3, ...}. Oznacza to po prostu, że każdy element w S odpowiada innemu elementowi w N .

Podział zbiorów na różne klasy może wydawać się naturalne: złóż wszystkie zestawy zawierające jeden element; wszystkie zestawy zawierające dwa elementy razem; ...; na koniec połącz wszystkie nieskończone zestawy i rozważ je jako mające ten sam rozmiar. Tego poglądu nie da się jednak obronić w ramach naturalnej definicji rozmiaru.

Aby to rozwinąć, potrzebujemy pojęcia bijekcji . Chociaż „bijection” może wydawać się pojęciem bardziej zaawansowanym niż liczba, zwykły rozwój matematyki w zakresie teorii mnogości definiuje funkcje przed liczbami, ponieważ są one oparte na znacznie prostszych zestawach. W tym miejscu pojawia się pojęcie bijekcji: zdefiniuj korespondencję

a 1, b ↔ 2, c ↔ 3

Ponieważ każdy element { a , b , c } jest sparowany z dokładnie jednym elementem {1, 2, 3} i odwrotnie, definiuje to bijekcję.

Uogólniamy teraz tę sytuację; możemy określić , że dwa zbiory są tej samej wielkości, wtedy i tylko wtedy, jeśli istnieje bijection między nimi. Dla wszystkich zbiorów skończonych daje nam to zwykłą definicję „tego samego rozmiaru”.

W przypadku zbiorów nieskończonych rozważmy zbiory A = {1, 2, 3, ... } , zbiór liczb całkowitych dodatnich , oraz B = {2, 4, 6, ... } , zbiór parzystych liczby naturalne. Twierdzimy, że zgodnie z naszą definicją zbiory te mają ten sam rozmiar, a zatem B jest przeliczalnie nieskończone. Przypomnijmy, że aby to udowodnić, musimy wykazać bijekcję między nimi. Można to osiągnąć za pomocą przypisania n ↔ 2 n , tak że

1 × 2, 2 × 4, 3 × 6, 4 × 8, ....

Podobnie jak we wcześniejszym przykładzie, każdy element A został sparowany z dokładnie jednym elementem B i na odwrót. Dlatego mają ten sam rozmiar. Jest to przykład zbioru o takim samym rozmiarze jak jeden z jego właściwych podzbiorów , co jest niemożliwe dla zbiorów skończonych.

Podobnie zbiór wszystkich uporządkowanych par liczb naturalnych ( iloczyn kartezjański dwóch zbiorów liczb naturalnych N × N ) jest przeliczalnie nieskończony, co można zobaczyć, podążając ścieżką podobną do tej na rysunku:

Funkcja parowania Cantora przypisuje jedną liczbę naturalną do każdej pary liczb naturalnych

Wynikowe mapowanie przebiega w następujący sposób:

0 (0, 0), 1 (1, 0), 2 (0, 1), 3 ↔ (2, 0), 4 (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), ....

To mapowanie obejmuje wszystkie takie uporządkowane pary.

Ta forma odwzorowania trójkątnego rekurencyjnie uogólnia się na n - krotki liczb naturalnych, tj. ( a ₁ , a ₂ , a ₃ , ..., a _n ) gdzie a _i oraz n są liczbami naturalnymi, poprzez wielokrotne mapowanie pierwszych dwóch elementów z n -tuple do liczby naturalnej. Na przykład (0, 2, 3) można zapisać jako ((0, 2), 3). Następnie (0, 2) mapuje do 5, więc ((0, 2), 3) mapuje do (5, 3), następnie (5, 3) mapuje do 39. Ponieważ inna krotka 2-, czyli para taka jak ( a , b ), odwzorowuje się na inną liczbę naturalną, wystarczy różnica między dwoma n-krotkami o jeden element, aby zapewnić odwzorowanie n-krotek na różne liczby naturalne. Czyli wstrzyknięcie ze zbioru n -krotek do zbioru liczb naturalnych N jest udowodnione. W przypadku zbioru n-krotek utworzonego przez iloczyn kartezjański skończenie wielu różnych zbiorów, każdy element w każdej krotce odpowiada liczbie naturalnej, więc każdą krotkę można zapisać w liczbach naturalnych, a następnie stosuje się tę samą logikę do udowodnienia twierdzenia .

Twierdzenie: iloczyn kartezjański o skończenie wielu zbiorów przeliczalnych jest przeliczalna.

Zbiór wszystkich liczb całkowitych Z i zbiór wszystkich liczb wymiernych Q może intuicyjnie wydawać się znacznie większy niż N . Ale wygląd może mylić. Jeśli para jest traktowana jako w liczniku i mianowniku z wulgarnym frakcji (ułamek w postaci a / b, w którym i

b ≠ 0 są liczbami całkowitymi), po czym dla każdej frakcji pozytywny, to może pochodzić z wyraźną liczbą naturalną odpowiadającej do niego. Ta reprezentacja obejmuje również liczby naturalne, ponieważ każda liczba naturalna jest również ułamkiem N /1. Możemy więc wywnioskować, że jest dokładnie tyle dodatnich liczb wymiernych, ile jest dodatnich liczb całkowitych. Odnosi się to również do wszystkich liczb wymiernych, jak widać poniżej.

Twierdzenie: Z (zbiór wszystkich liczb całkowitych) i Q (zbiór wszystkich liczb wymiernych) są przeliczalne.

W podobny sposób zbiór liczb algebraicznych jest policzalny.

Czasami przydatne jest więcej niż jedno mapowanie: zbiór A, który ma być pokazany jako policzalny, jest mapowany jeden do jednego (wstrzykiwanie) do innego zbioru B, a następnie A okazuje się policzalny, jeśli B jest mapowany jeden do jednego do zbioru liczby naturalne. Na przykład zbiór dodatnich liczb wymiernych można łatwo odwzorować jeden do jednego na zbiór par liczb naturalnych (2-krotki), ponieważ p / q odwzorowuje ( p , q ). Ponieważ zbiór par liczb naturalnych jest odwzorowany jeden do jednego (właściwie jeden do jednego lub bijekcja) do zbioru liczb naturalnych, jak pokazano powyżej, dodatni zbiór liczb wymiernych jest udowodniony jako przeliczalny.

Twierdzenie: Każdy skończony związek z zbiór przeliczalny jest przeliczalny.

Mając świadomość, że istnieje niezliczona ilość zestawów, możemy się zastanawiać, czy ten ostatni wynik można posunąć dalej. Odpowiedź brzmi „tak” i „nie”, możemy ją rozszerzyć, ale w tym celu musimy przyjąć nowy aksjomat.

Twierdzenie: (Zakładając aksjomat wyboru policzalnego ) Suma policzalnych zbiorów przeliczalnych jest policzalna.

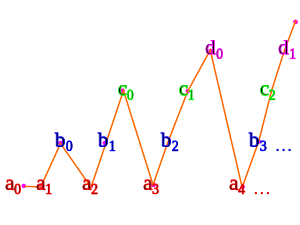
Na przykład dane zbiory przeliczalne a , b , c , ...

Enumeracja dla policzalnej liczby zbiorów policzalnych

Korzystając z wariantu wyliczenia trójkątnego, który widzieliśmy powyżej:

a ₀ mapuje do 0
A ₁ mapuje do 1
b ₀ mapuje do 2
a ₂ mapy do 3
b ₁ mapuje do 4
c ₀ mapuje do 5
A ₃ mapy do 6
b ₂ mapy do 7
c ₁ mapuje do 8
d ₀ mapuje do 9
a ₄ mapy do 10
...

Działa to tylko wtedy, gdy zbiory a , b , c , ... są rozłączne . Jeśli nie, to suma jest jeszcze mniejsza i dlatego jest również policzalna przez poprzednie twierdzenie.

Potrzebujemy aksjomatu policzalnego wyboru, aby indeksować wszystkie zbiory a , b , c , ... jednocześnie.

Twierdzenie: Zbiór wszystkich ciągów liczb naturalnych o skończonej długości jest przeliczalny.

Ten zbiór jest połączeniem sekwencji o długości 1, sekwencji o długości 2, sekwencji o długości 3, z których każdy jest zbiorem policzalnym (skończony iloczyn kartezjański). Mówimy więc o policzalnej unii zbiorów policzalnych, która jest policzalna przez poprzednie twierdzenie.

Twierdzenie: Zbiór wszystkich skończonych podzbiorów liczb naturalnych jest przeliczalny.

Elementy dowolnego skończonego podzbioru można uporządkować w skończony ciąg. Istnieje tylko przeliczalnie wiele skończonych ciągów, więc istnieje tylko przeliczalnie wiele skończonych podzbiorów.

Twierdzenie: Niech S i T będą zbiorami.

Jeżeli funkcja f : S → T jest iniekcyjna i T jest policzalna, to S jest policzalne.
Jeżeli funkcja g : S → T jest surjektywna i S jest policzalna, to T jest policzalne.

Wynikają one z definicji zbioru przeliczalnego jako funkcji iniektywnych/surjektywnych.

Twierdzenie Cantora głosi, że jeśli A jest zbiorem, a P ( A ) jest jego zbiorem potęgowym , tj. zbiorem wszystkich podzbiorów A , to nie ma funkcji surjektywnej od A do P ( A ). Dowód podano w artykule Twierdzenie Cantora . Bezpośrednią konsekwencją tego i powyższego twierdzenia podstawowego jest:

Twierdzenie: Zbiór P ( N ) jest niepoliczalny; tj. jest niepoliczalna .

Dla rozwinięcia tego wyniku zobacz argument diagonalny Cantora .

Zbiór liczb rzeczywistych jest niepoliczalny, podobnie jak zbiór wszystkich nieskończonych ciągów liczb naturalnych.

Minimalny model teorii mnogości jest policzalny

Jeśli istnieje zbiór, który jest modelem standardowym (patrz model wewnętrzny ) teorii mnogości ZFC, to istnieje minimalny model standardowy ( patrz Wszechświat konstruowalny ). Twierdzenie Löwenheima-Skolema można wykorzystać do wykazania, że ten minimalny model jest policzalny. Fakt, że pojęcie „nieprzeliczalności” ma sens nawet w tym modelu, a w szczególności, że model M zawiera elementy, które są:

podzbiory M , stąd policzalne,
ale niepoliczalne z punktu widzenia M ,

był postrzegany jako paradoksalny we wczesnych dniach teorii mnogości, zobacz paradoks Skolema po więcej.

Minimalny model standardowy zawiera wszystkie liczby algebraiczne i wszystkie efektywnie obliczalne liczby przestępne , a także wiele innych rodzajów liczb.

Razem zamówienia

Zestawy policzalne można zamawiać w

całości na różne sposoby, na przykład:

Dobrze zamówienia (patrz również liczba porządkowa ):
- Zwykła kolejność liczb naturalnych (0, 1, 2, 3, 4, 5, ...)
- Liczby całkowite w kolejności (0, 1, 2, 3, ...; −1, −2, −3, ...)
Inne ( niezbyt dobrze zamówienia):
- Zwykła kolejność liczb całkowitych (..., -3, -2, -1, 0, 1, 2, 3, ...)
- Zwykła kolejność liczb wymiernych (nie może być jawnie zapisana jako uporządkowana lista!)

W obu przykładach dobrze uporządkowanych tutaj każdy podzbiór ma najmniejszy element ; aw obu przykładach rzędów innych niż dobrze niektóre podzbiory nie mają najmniejszego elementu . To jest kluczowa definicja, która określa, czy zamówienie całkowite jest również dobrem.

Zobacz też

Uwagi

Cytaty

Bibliografia

Apostol, Tom M. (czerwiec 1969), rachunek różniczkowy wielu zmiennych i algebra liniowa z aplikacjami , Rachunek, 2 (2nd ed.), New York: John Wiley + Sons, ISBN 978-0-471-00007-5
Avelsgaard, Carol (1990), Podstawy zaawansowanej matematyki , Scott, Foresman and Company, ISBN 0-673-38152-8
Kantor Georg (1878), „Ein Beitrag zur Mannigfaltigkeitslehre” , Journal für die Reine und Angewandte Mathematik , 1878 (84): 242–248, doi : 10.1515/crelle-1878-18788413
Ferreirós, José (2007), Labirynt myśli: historia teorii mnogości i jej rola w myśli matematycznej (2. poprawione wyd.), Birkhäuser, ISBN 978-3-7643-8349-7
Fletcher, Piotr; Patty, C. Wayne (1988), Podstawy Wyższej Matematyki , Boston: PWS-KENT Publishing Company, ISBN 0-87150-164-3
Halmos, Paul R. (1960), Naiwna teoria mnogości , D. Van Nostrand Company, IncPrzedruk Springer-Verlag, New York, 1974. ISBN 0-387-90092-6 (wydanie Springer-Verlag). Przedruk Martino Fine Books, 2011. ISBN 978-1-61427-131-4 (wydanie w miękkiej oprawie).
Kamke, Erich (1950), Teoria zbiorów , seria Dover w matematyce i fizyce , New York: Dover, ISBN 978-0486601410
Lang, Serge (1993), Analiza rzeczywista i funkcjonalna , Berlin, New York: Springer-Verlag, ISBN 0-387-94001-4
Rudin, Walter (1976), Zasady analizy matematycznej , New York: McGraw-Hill, ISBN 0-07-054235-X
Tao, Terence (2016). „Zbiory nieskończone” . Analiza I (wyd. trzecie). Singapur: Springer. s. 181-210. Numer ISBN 978-981-10-1789-6.

Languages

In other projects