Metoda gradientu sprzężonego - Conjugate gradient method

Porównanie zbieżności gradientu opadania z optymalną wielkością kroku (na zielono) i wektorem sprzężonym (na czerwono) w celu zminimalizowania funkcji kwadratowej związanej z danym układem liniowym. Gradient sprzężony, zakładając arytmetykę dokładną, jest zbieżny w co najwyżej n krokach, gdzie n jest wielkością macierzy układu (tu n  = 2).

W matematyce The koniugat gradient metoda jest algorytm do numerycznego rozwiązania poszczególnych systemów równań liniowych , to znaczy te, których matryca jest dodatnio określony . Metoda gradientu sprzężonego jest często implementowana jako algorytm iteracyjny , mający zastosowanie do rzadkich systemów, które są zbyt duże, aby można je było obsłużyć przez implementację bezpośrednią lub inne metody bezpośrednie, takie jak rozkład Cholesky'ego . Duże rzadkie układy często powstają podczas numerycznego rozwiązywania równań różniczkowych cząstkowych lub problemów optymalizacyjnych.

Metodę gradientu sprzężonego można również wykorzystać do rozwiązywania problemów optymalizacji bez ograniczeń , takich jak minimalizacja energii . Jest powszechnie przypisywany Magnusowi Hestenesowi i Eduardowi Stiefelowi , którzy zaprogramowali go na Z4 i intensywnie badali.

Sposób biconjugate gradientu zapewnia uogólnienie do matryc niesymetrycznej. Różne nieliniowe metody gradientów sprzężonych poszukują minimów równań nieliniowych i funkcji celu czarnoskrzynkowego.

Opis problemu, którego dotyczą gradienty sprzężone

Załóżmy, że chcemy rozwiązać układ równań liniowych

${\ Displaystyle \ mathbf {A} \ mathbf {x} = \ mathbf {b}}$

dla wektora , gdzie znana macierz jest symetryczna (tj . ^AT = A ), dodatnio określona (tj. x ^T Ax > 0 dla wszystkich niezerowych wektorów w R ⁿ ) i rzeczywista , a także jest znana. Unikalne rozwiązanie tego systemu określamy symbolem . ${\displaystyle \mathbf {x}}$${\displaystyle n\razy n}$${\ Displaystyle \ mathbf {A}}$${\displaystyle \mathbf {x}}$${\displaystyle \mathbf {b}}$${\ Displaystyle \ mathbf {x} _ {*}}$

Wyprowadzenie jako metoda bezpośrednia

Metodę gradientu sprzężonego można wyprowadzić z kilku różnych perspektyw, w tym ze specjalizacji metody kierunku sprzężonego do optymalizacji oraz wariacji iteracji Arnoldiego / Lanczosa dla problemów z wartościami własnymi . Pomimo różnic w ich podejściach, te derywacje mają wspólny temat — udowadnianie ortogonalności reszt i koniugacji kierunków wyszukiwania. Te dwie właściwości są kluczowe dla opracowania dobrze znanego zwięzłego sformułowania metody.

Mówimy, że dwa niezerowe wektory u i v są sprzężone (w odniesieniu do ) jeśli ${\ Displaystyle \ mathbf {A}}$

${\ Displaystyle \ mathbf {u} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {v} = 0.}$

Ponieważ jest symetryczny i dodatnio określony, lewa strona definiuje iloczyn skalarny${\ Displaystyle \ mathbf {A}}$

${\ Displaystyle \ mathbf {u} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {v} = \ langle \ mathbf {u} \ mathbf {v} \ rangle _ {\ mathbf {A}} :=\langle \mathbf {A} \mathbf {u} ,\mathbf {v} \rangle =\langle \mathbf {u} ,\mathbf {A} ^{\mathsf {T}}\mathbf {v} \ rangle =\langle \mathbf {u},\mathbf {A} \mathbf {v} \rangle}$

Dwa wektory są sprzężone wtedy i tylko wtedy, gdy są ortogonalne względem tego produktu wewnętrznego. Bycie sprzężonym jest relacją symetryczną: jeśli jest sprzężony z , to jest sprzężony z . Przypuszczam, że ${\displaystyle \mathbf {u}}$${\displaystyle \mathbf {v}}$${\displaystyle \mathbf {v}}$${\displaystyle \mathbf {u}}$

${\ Displaystyle P = \ {\ mathbf {p} _ {1} \ kropki \ mathbf {p} _ {n} \}}$

jest zbiorem wzajemnie sprzężonych wektorów względem , tj. dla wszystkich . Następnie tworzy podstawę dla i można wyrazić roztworu o na tej podstawie: ${\ Displaystyle n}$${\ Displaystyle \ mathbf {A}}$${\ Displaystyle \ mathbf {p} _ {i} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {p} _ {j} = 0}$${\displaystyle i\neqj}$${\displaystyle P}$${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle \ mathbf {x} _ {*}}$${\ Displaystyle \ mathbf {topór} = \ mathbf {b}}$

${\ Displaystyle \ mathbf {x} _ {*} = \ suma _ {i = 1} ^ {n} \ alfa _ {i} \ mathbf {p} _ {i} \ prawostrzałka \ mathbf {A} \ mathbf { x} _{*}=\sum _{i=1}^{n}\alpha _{i}\mathbf {A} \mathbf {p} _{i}.}$

Mnożenie lewej strony przez plony ${\ Displaystyle \ mathbf {p} _ {k} ^ {\ mathsf {T}}}$

${\ Displaystyle \ mathbf {p} _ {k} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {x} _ {*} = \ suma _ {i = 1} ^ {n} \ alfa _ {i}\mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{i}\Rightarrow \mathbf {p} _{k}^{\mathsf { T}}\mathbf {b} =\sum _{i=1}^{n}\alpha _{i}\left\langle \mathbf {p} _{k},\mathbf {p} _{i} \right\rangle _{\mathbf {A} }=\alpha _{k}\left\langle \mathbf {p} _{k},\mathbf {p} _{k}\right\rangle _{\mathbf {A} }\Strzałka w prawo }$

${\ Displaystyle \ alfa _ {k} = {\ Frac {\ langle \ mathbf {p} _ {k} \ mathbf {b} \ rangle} {\ langle \ mathbf {p} _ {k} \ mathbf { p} _{k}\rangle _{\mathbf {A} }}}.}$

Daje to następującą metodę rozwiązania równania Ax = b : znajdź sekwencję kierunków sprzężonych, a następnie oblicz współczynniki . ${\ Displaystyle n}$${\ Displaystyle \ alfa _ {k}}$

Jako metoda iteracyjna

Jeśli starannie dobierzemy wektory sprzężone , możemy nie potrzebować ich wszystkich, aby uzyskać dobre przybliżenie rozwiązania . Tak więc, chcemy traktować metodę gradientu sprzężonego jako metodę iteracyjną. Pozwala nam to również w przybliżeniu rozwiązać systemy, w których n jest tak duże, że metoda bezpośrednia zajęłaby zbyt dużo czasu. ${\ Displaystyle \ mathbf {p} _ {k}}$${\ Displaystyle \ mathbf {x} _ {*}}$

Początkowe przypuszczenie dla x _∗ oznaczamy przez x ₀ (możemy założyć bez utraty ogólności, że x ₀ = 0 , w przeciwnym razie rozważmy zamiast tego system Az = b − Ax ₀ ). Zaczynając od x ₀ szukamy rozwiązania iw każdej iteracji potrzebujemy metryki, która powie nam, czy jesteśmy bliżej rozwiązania x _∗ (którego nie znamy). Ta metryka wynika z faktu, że rozwiązanie x _∗ jest również unikalnym minimalizatorem następującej funkcji kwadratowej

${\ Displaystyle f (\ mathbf {x} ) = {\ tfrac {1} {2}} \ mathbf {x} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {x} - \ mathbf {x } ^{\mathsf {T}}\mathbf {b} ,\qquad \mathbf {x} \in \mathbf {R} ^{n}\,.}$

Istnienie unikatowego minimalizatora jest oczywiste, gdyż jego drugą pochodną dana jest symetryczna macierz dodatnio określona

${\ Displaystyle \ nabla ^ {2} f (\ mathbf {x} ) = \ mathbf {A} \,,}$

i że minimalizator (użyj D f ( x )=0) rozwiązuje początkowy problem jest oczywiste z jego pierwszej pochodnej

${\ Displaystyle \ nabla f (\ mathbf {x} ) = \ mathbf {A} \ mathbf {x} - \ mathbf {b} \}.$

Sugeruje to przyjęcie pierwszego wektora bazowego p ₀ jako ujemnego gradientu f przy x = x ₀ . Gradient f jest równy Ax − b . Zaczynając od początkowego przypuszczenia x ₀ , oznacza to, że bierzemy p ₀ = b − Ax ₀ . Pozostałe wektory w bazie będą sprzężone z gradientem, stąd nazwa metoda gradientu sprzężonego . Zauważ, że p ₀ jest również resztą dostarczoną przez ten początkowy krok algorytmu.

Niech r _k będzie resztą na k- tym kroku:

${\ Displaystyle \ mathbf {r} _ {k} = \ mathbf {b} - \ mathbf {topór} _ {k}.}$

Jak zaobserwowano powyżej, jest to ujemny gradient at , więc metoda gradientu opadania wymagałaby poruszania się w kierunku r _k . Tutaj jednak nalegamy, aby kierunki były ze sobą sprzężone. Praktycznym sposobem na wymuszenie tego jest wymaganie, aby następny kierunek wyszukiwania był zbudowany na podstawie bieżącej pozostałości i wszystkich poprzednich kierunków wyszukiwania. Ograniczenie sprzężenia jest ograniczeniem typu ortonormalnego, a zatem algorytm można postrzegać jako przykład ortonormalizacji Grama-Schmidta . Daje to następujące wyrażenie: ${\ Displaystyle \ mathbf {r} _ {k}}$${\displaystyle f}$${\ Displaystyle \ mathbf {x} _ {k}}$${\ Displaystyle \ mathbf {p} _ {k}}$

${\ Displaystyle \ mathbf {p} _ {k} = \ mathbf {r} _ {k} - \ suma _ {i <k} {\ Frac {\ mathbf {p} _ {i} ^ {\ mathsf {T }}\mathbf {A} \mathbf {R} _{k}}{\mathbf {p} _{i}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{i}} }\mathbf {p} _{i}}$

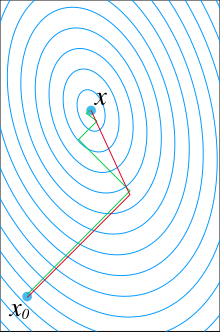
(patrz rysunek na górze artykułu, aby zobaczyć wpływ ograniczenia koniugacji na zbieżność). Idąc w tym kierunku, kolejną optymalną lokalizację podaje

${\ Displaystyle \ mathbf {x} _ {k + 1} = \ mathbf {x} _ {k} + \ alfa _ {k} \ mathbf {p} _ {k}}$

z

${\ Displaystyle \ alfa _ {k} = {\ Frac {\ mathbf {p} _ {k} ^ {\ mathsf {T}} (\ mathbf {b} - \ mathbf {topór} _ {k})} { \mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}={\frac {\mathbf {p} _{k}^{\ mathsf {T}}\mathbf {R} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}, }$

gdzie ostatnia równość wynika z definicji . Wyrażenie for można wyprowadzić, podstawiając wyrażenie x _{k +1} do f i minimalizując je wrt${\ Displaystyle \ mathbf {r} _ {k}}$${\ Displaystyle \ alfa _ {k}}$${\ Displaystyle \ alfa _ {k}}$

${\ Displaystyle {\ zacząć {wyrównany} f (\ mathbf {x} _ {k + 1}) i = f (\ mathbf {x} _ {k} + \ alfa _ {k} \ mathbf {p} _ { k})=:g(\alpha _{k})\\g'(\alpha _{k})&{\overset {!}{=}}0\quad \Rightarrow \quad \alpha _{k} ={\frac {\mathbf {p} _{k}^{\mathsf {T}}(\mathbf {b} -\mathbf {topór} _{k})}{\mathbf {p} _{k} ^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}\,.\end{wyrównany}}}$

Powstały algorytm

Powyższy algorytm daje najprostsze wyjaśnienie metody gradientu sprzężonego. Pozornie wspomniany algorytm wymaga przechowywania wszystkich poprzednich kierunków wyszukiwania i wektorów reszt, a także wielu mnożeń macierz-wektor, a zatem może być kosztowny obliczeniowo. Jednak bliższa analiza algorytmu pokazuje, że jest ortogonalny do , tj. dla i ≠ j. I jest -ortogonalna do , czyli do . Można to uznać, że wraz z postępem algorytmu i obejmuje tę samą podprzestrzeń Kryłowa . Gdzie tworzą bazę ortogonalną w odniesieniu do standardowego iloczynu skalarnego i tworzą bazę ortogonalną w odniesieniu do iloczynu skalarnego indukowanego przez . Dlatego można ją traktować jako rzutowanie na podprzestrzeń Kryłowa. ${\ Displaystyle \ mathbf {r} _ {i}}$${\ Displaystyle \ mathbf {r} _ {j}}$${\ Displaystyle \ mathbf {R} _ {i} ^ {\ mathsf {T}} \ mathbf {R} _ {j} = 0}$${\ Displaystyle \ mathbf {p} _ {i}}$${\ Displaystyle \ mathbf {A}}$${\ Displaystyle \ mathbf {p} _ {j}}$${\ Displaystyle \ mathbf {p} _ {i} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {p} _ {j} = 0}$${\displaystyle i\neqj}$${\ Displaystyle \ mathbf {p} _ {i}}$${\ Displaystyle \ mathbf {r} _ {i}}$${\ Displaystyle \ mathbf {r} _ {i}}$${\ Displaystyle \ mathbf {p} _ {i}}$${\ Displaystyle \ mathbf {A}}$${\ Displaystyle \ mathbf {x} _ {k}}$${\displaystyle \mathbf {x}}$

Poniżej opisano szczegółowo algorytm rozwiązywania Ax = b, gdzie jest rzeczywistą, symetryczną, dodatnio określoną macierzą. Wektor wejściowy może być przybliżonym rozwiązaniem początkowym lub 0 . Jest to inne sformułowanie dokładnej procedury opisanej powyżej. ${\ Displaystyle \ mathbf {A}}$${\ Displaystyle \ mathbf {x} _{0}}$

${\ Displaystyle {\ zacząć {wyrównany} i \ mathbf {R} _ {0}: = \ mathbf {b} - \ mathbf {topór} _ {0} \ \ i {\ hbox {jeśli}} \ mathbf {o } _{0}{\text{ jest wystarczająco mały, a następnie zwróć }}\mathbf {x} _{0}{\text{ jako wynik}}\\&\mathbf {p} _{0}:=\ mathbf {r} _{0}\\&k:=0\\&{\text{powtórz}}\\&\qquad \alpha _{k}:={\frac {\mathbf {r} _{k} ^{\mathsf {T}}\mathbf {r} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {Ap} _{k}}}\\& \qquad \mathbf {x} _{k+1}:=\mathbf {x} _{k}+\alpha _{k}\mathbf {p} _{k}\\&\qquad \mathbf {r} _{k+1}:=\mathbf {r} _{k}-\alpha _{k}\mathbf {Ap} _{k}\\&\qquad {\hbox{if }}\mathbf {r} _{k+1}{\text{ jest wystarczająco małe, to wyjście z pętli}}\\&\qquad \beta _{k}:={\frac {\mathbf {r} _{k+1}^{\ mathsf {T}}\mathbf {r} _{k+1}}{\mathbf {r} _{k}^{\mathsf {T}}\mathbf {r} _{k}}}\\&\ qquad \mathbf {p} _{k+1}:=\mathbf {r} _{k+1}+\beta _{k}\mathbf {p} _{k}\\&\qquad k:=k +1\\&{\text{koniec powtórz}}\\&{\text{powrót }}\mathbf {x} _{k+1}{\text{ jako wynik}}\end{wyrównany}}}$

Jest to najczęściej używany algorytm. Ten sam wzór na β _k jest również stosowany w nieliniowej metodzie gradientu sprzężonego Fletchera-Reevesa .

Ponowne uruchamianie

Zauważmy, że jest to obliczane przez metodę gradientu opadania stosowaną do . Ustawienie w podobny sposób sprawiłoby, że obliczone metodą gradientu opadania z , tj. może być użyte jako prosta implementacja ponownego uruchomienia iteracji gradientu sprzężonego. Ponowne uruchomienie może spowolnić zbieżność, ale może poprawić stabilność, jeśli metoda gradientu sprzężonego nie będzie działać, np. z powodu błędu zaokrąglenia . ${\ Displaystyle \ mathbf {x} _ {1}}$${\ Displaystyle \ mathbf {x} _{0}}$${\ Displaystyle \ beta _ {k} = 0}$${\ Displaystyle \ mathbf {x} _ {k + 1}}$${\ Displaystyle \ mathbf {x} _ {k}}$

Wyraźne obliczenia rezydualne

Wzory i , które zarówno w dokładnym chwyt arytmetyki, sprawiają, że wzory i matematycznie równoważne. Pierwszy jest używany w algorytmie, aby uniknąć dodatkowego mnożenia przez, ponieważ wektor jest już obliczony do oceny . Ta ostatnia może być bardziej dokładna, zastępując jawną kalkulację za niejawną rekurencją podlegającą akumulacji błędów zaokrąglenia , a zatem jest zalecana do sporadycznej oceny. ${\ Displaystyle \ mathbf {x} _ {k + 1}: = \ mathbf {x} _ {k} + \ alfa _ {k} \ mathbf {p} _ {k}}$${\ Displaystyle \ mathbf {r} _ {k}: = \ mathbf {b} - \ mathbf {topór} _ {k}}$${\ Displaystyle \ mathbf {r} _ {k + 1}: = \ mathbf {r} _ {k} - \ alfa _ {k} \ mathbf {ap} _ {k}}$${\ Displaystyle \ mathbf {r} _ {k + 1}: = \ mathbf {b} - \ mathbf {topór} _ {k + 1}}$${\ Displaystyle \ mathbf {A}}$${\ Displaystyle \ mathbf {ap} _ {k}}$${\ Displaystyle \ alfa _ {k}}$${\ Displaystyle \ mathbf {r} _ {k + 1}: = \ mathbf {b} - \ mathbf {topór} _ {k + 1}}$

Norma wartości rezydualnej jest zwykle używana do kryteriów zatrzymania. Norma jawnej reszty zapewnia gwarantowany poziom dokładności zarówno w arytmetyce dokładnej, jak iw obecności błędów zaokrągleń , gdzie zbieżność naturalnie ulega stagnacji. W przeciwieństwie do tego wiadomo , że implicytna reszta ma coraz mniejszą amplitudę znacznie poniżej poziomu błędów zaokrągleń, a zatem nie można jej użyć do określenia stagnacji zbieżności. ${\ Displaystyle \ mathbf {r} _ {k + 1}: = \ mathbf {b} - \ mathbf {topór} _ {k + 1}}$${\ Displaystyle \ mathbf {r} _ {k + 1}: = \ mathbf {r} _ {k} - \ alfa _ {k} \ mathbf {ap} _ {k}}$

Obliczanie alfa i beta

W algorytmie, α _k jest dobrana tak, że jest prostopadły do . Mianownik jest uproszczony z ${\ Displaystyle \ mathbf {r} _ {k+1}}$${\ Displaystyle \ mathbf {r} _ {k}}$

${\ Displaystyle \ alfa _ {k} = {\ Frac {\ mathbf {R} _ {k} ^ {\ mathsf {T}} \ mathbf {R} _ {k}} {\ mathbf {R} _ {k }^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}={\frac {\mathbf {r} _{k}^{\mathsf {T}}\mathbf { r} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {Ap} _{k}}}}$

od . Β _k jest tak dobrany, że jest sprzężony z . Początkowo β _k jest ${\ Displaystyle \ mathbf {r} _ {k + 1} = \ mathbf {p} _ {k + 1} - \ mathbf {\ beta} _ {k} \ mathbf {p} _ {k}}$${\ Displaystyle \ mathbf {p} _ {k+1}}$${\ Displaystyle \ mathbf {p} _ {k}}$

${\ Displaystyle \ beta _ {k} = - {\ Frac {\ mathbf {r} _ {k + 1} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {p} _ {k}} \mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}}$

za pomocą

${\ Displaystyle \ mathbf {r} _ {k + 1} = \ mathbf {r} _ {k} - \ alfa _ {k} \ mathbf {A} \ mathbf {p} _ {k}}$

i równoważnie

${\ Displaystyle \ mathbf {A} \ mathbf {p} _ {k} = {\ Frac {1} {\ alfa _ {k}}} (\ mathbf {R} _ {k} - \ mathbf {R} _ {k+1}),}$

licznik β _k jest przepisany jako

${\ Displaystyle \ mathbf {r} _ {k + 1} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {p} _ {k} = {\ Frac {1} {\ alfa _ {k} }}\mathbf {r} _{k+1}^{\mathsf {T}}(\mathbf {r} _{k}-\mathbf {r} _{k+1})=-{\frac { 1}{\alpha _{k}}}\mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {r} _{k+1}}$

ponieważ i są z założenia ortogonalne. Mianownik jest przepisany jako ${\ Displaystyle \ mathbf {r} _ {k+1}}$${\ Displaystyle \ mathbf {r} _ {k}}$

${\ Displaystyle \ mathbf {p} _ {k} ^ {\ mathsf {T}} \ mathbf {A} \ mathbf {p} _ {k} = (\ mathbf {r} _ {k} + \ beta _ { k-1}\mathbf {p} _{k-1})^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}={\frac {1}{\alpha _{ k}}}\mathbf {r} _{k}^{\mathsf {T}}(\mathbf {r} _{k}-\mathbf {r} _{k+1})={\frac {1 }{\alpha _{k}}}\mathbf {r} _{k}^{\mathsf {T}}\mathbf {r} _{k}}$

używając, że kierunki wyszukiwania p _k są sprzężone i ponownie, że reszty są ortogonalne. Daje to β w algorytmie po anulowaniu α _k .

Przykładowy kod w MATLAB / GNU Octave

function x = conjgrad(A, b, x)
    r = b - A * x;
    p = r;
    rsold = r' * r;

    for i = 1:length(b)
        Ap = A * p;
        alpha = rsold / (p' * Ap);
        x = x + alpha * p;
        r = r - alpha * Ap;
        rsnew = r' * r;
        if sqrt(rsnew) < 1e-10
              break
        end
        p = r + (rsnew / rsold) * p;
        rsold = rsnew;
    end
end

Przykład liczbowy

Rozważmy układ liniowy Ax = b dany przez

${\ Displaystyle \ mathbf {A} \ mathbf {x} = {\ zacząć {bmatrix} 4 i 1 \ \ 1 i 3 \ koniec {bmatrix}} {\ zacząć {bmatrix} x_ {1} \ \ x_ {2} \ koniec {bmatrix} }}={\begin{bmatryca}1\\2\end{bmatryca}},}$

wykonamy dwa kroki metody gradientu sprzężonego, zaczynając od wstępnego zgadywania

${\ Displaystyle \ mathbf {x} _ {0} = {\ zacząć {bmatrix} 2 \ \ 1 \ koniec {bmatrix}}}$

w celu znalezienia przybliżonego rozwiązania systemu.

Rozwiązanie

Dla porównania, dokładne rozwiązanie to

${\ Displaystyle \ mathbf {x} = {\ zacząć {bmatrix} {\ Frac {1} {11}} \ \ \ \ {\ Frac {7} {11}} \ koniec {bmatrix}} \ około {\ zacząć {bmatryca}0,0909\\\\0.6364\koniec{bmatrycy}}}$

Naszym pierwszym krokiem jest obliczenie wektora resztkowego r ₀ związanego z x ₀ . Ta reszta jest obliczana ze wzoru r ₀ = b - Ax ₀ , a w naszym przypadku jest równa

${\ Displaystyle \ mathbf {r} _ {0} = {\ zacznij {bmatrix} 1 \ \ 2 \ koniec {bmatrix}} - {\ zacznij {bmatrix} 4 i 1 \ \ 1 i 3 \ koniec {bmatrix}} {\ zacznij { bmatrix}2\\1\end{bmatrix}}={\begin{bmatrix}-8\\-3\end{bmatrix}}=\mathbf {p} _{0}.}$

Ponieważ jest to pierwsza iteracja, użyjemy wektora resztkowego r ₀ jako naszego początkowego kierunku przeszukiwania p ₀ ; sposób doboru p _k zmieni się w kolejnych iteracjach.

Teraz obliczamy skalar α ₀ używając zależności

${\ Displaystyle \ alfa _ {0} = {\ Frac {\ mathbf {R} _ {0} ^ {\ mathsf {T}} \ mathbf {R} _ {0}} {\ mathbf {p} _ {0 }^{\mathsf {T}}\mathbf {Ap} _{0}}}={\frac {{\begin{bmatrix}-8&-3\end{bmatrix}}{\begin{bmatrix}-8\ \-3\end{bmatrix}}}{{\begin{bmatrix}-8&-3\end{bmatrix}}{\begin{bmatrix}4&1\\1&3\end{bmatrix}}{\begin{bmatrix}- 8\\-3\end{bmatryca}}}}={\frac {73}{331}}.}$

Możemy teraz obliczyć x ₁ za pomocą wzoru

${\ Displaystyle \ mathbf {x} _ {1} = \ mathbf {x} _ {0}+ \ alfa _ {0} \ mathbf {p} _ {0} = {\ zacząć {bmatrix} 2 \ \ 1 \ end{bmatrix}}+{\frac {73}{331}}{\begin{bmatrix}-8\\-3\end{bmatrix}}={\begin{bmatrix}0.2356\\0.3384\end{bmatrix} }.}$

Ten wynik kończy pierwszą iterację, wynikiem jest „ulepszone” przybliżone rozwiązanie systemu, x ₁ . Możemy teraz przejść dalej i obliczyć następny wektor resztkowy r ₁ ze wzoru

${\ Displaystyle \ mathbf {R} _ {1} = \ mathbf {R} _ {0}-\ alfa _ {0} \ mathbf {A} \ mathbf {p} _ {0} = {\ zacząć {bmatrix} -8\\-3\end{bmacierz}}-{\frac {73}{331}}{\begin{bmacierz}4&1\\1&3\end{bmacierz}}{\begin{bmacierz}-8\\- 3\koniec{bmatrycy}}={\początek{bmatrycy}-0,2810\\0.7492\koniec{bmatrycy}}.}$

Następnym krokiem w tym procesie jest obliczenie wartości skalarnej β _{0 ,} która zostanie ostatecznie użyta do określenia następnego kierunku przeszukiwania p ₁ .

${\ Displaystyle \ beta _ {0} = {\ Frac {\ mathbf {R} _ {1} ^ {\ mathsf {T}} \ mathbf {R} _ {1}} {\ mathbf {R} _ {0 }^{\mathsf {T}}\mathbf {r} _{0}}}={\frac {{\begin{bmacierz}-0,2810&0,7492\koniec{bmacierzy}}{\begin{bmacierz}-0,2810 \\0.7492\end{bmacierz}}}{{\begin{bmatrycy}-8&-3\end{bmatrycy}}{\begin{bmacierzy}-8\\-3\end{bmatrycy}}}=0.0088. }$

Teraz, używając tego skalaru β ₀ , możemy obliczyć następny kierunek przeszukiwania p ₁ używając zależności

${\ Displaystyle \ mathbf {p} _ {1} = \ mathbf {r} _ {1} + \ beta _ {0} \ mathbf {p} _ {0} = {\ zacząć {bmatrix} -0,2810 \ \ 0,7492 \end{bmatrix}}+0.0088{\begin{bmatrix}-8\\-3\end{bmatrix}}={\begin{bmatrix}-0,3511\\0.7229\end{bmatrix}}.}$

Teraz obliczamy skalar α ₁ przy użyciu naszego nowo uzyskanego p ₁ przy użyciu tej samej metody, która została użyta dla α ₀ .

${\ Displaystyle \ alfa _ {1} = {\ Frac {\ mathbf {R} _ {1} ^ {\ mathsf {T}} \ mathbf {R} _ {1}} {\ mathbf {p} _ {1 }^{\mathsf {T}}\mathbf {Ap} _{1}}}={\frac {{\begin{bmacierz}-0,2810&0,7492\koniec{bmatrycy}}{\begin{bmatrycy}-0,2810 \\0.7492\end{bmatrix}}}{{\begin{bmatrix}-0.3511&0.7229\end{bmatrix}}{\begin{bmatrix}4&1\\1&3\end{bmatrix}}{\begin{bmatrix} -0,3511\\0.7229\koniec{bmatrycy}}}=0,4122.}$

Na koniec znajdujemy x ₂ przy użyciu tej samej metody, która została użyta do znalezienia x ₁ .

${\ Displaystyle \ mathbf {x} _ {2} = \ mathbf {x} _ {1} + \ alfa _ {1} \ mathbf {p} _ {1} = {\ zacząć {bmatrix} 0,2356 \ \ 0,3384 \ end{bmatrix}}+0.4122{\begin{bmatrix}-0.3511\\0.7229\end{bmatrix}}={\begin{bmatrix}0.0909\\0.6364\end{bmatrix}}.}$

Wynik, x ₂ , jest „lepszym” przybliżeniem rozwiązania systemowego niż x ₁ i x ₀ . Gdyby w tym przykładzie zastosowano arytmetykę dokładną zamiast ograniczonej precyzji, to teoretycznie dokładne rozwiązanie zostałoby osiągnięte po n = 2 iteracjach ( n jest porządkiem systemu).

Właściwości konwergencji

Metodę gradientu sprzężonego można teoretycznie traktować jako metodę bezpośrednią, ponieważ przy braku błędu zaokrąglenia daje dokładne rozwiązanie po skończonej liczbie iteracji, która nie jest większa niż rozmiar macierzy. W praktyce nigdy nie uzyskuje się dokładnego rozwiązania, ponieważ metoda gradientu sprzężonego jest niestabilna w odniesieniu do nawet małych perturbacji, np. większość kierunków nie jest w praktyce sprzężona, ze względu na degeneracyjny charakter generowania podprzestrzeni Kryłowa.

Jako metoda iteracyjna, metoda gradientu sprzężonego monotonicznie (w normie energetycznej) poprawia przybliżenia do dokładnego rozwiązania i może osiągnąć wymaganą tolerancję po stosunkowo niewielkiej (w porównaniu do wielkości problemu) liczbie iteracji. Poprawa jest zazwyczaj liniowa, a jej szybkość jest określona przez numer stanu macierzy systemu : im większa , tym wolniejsza poprawa. ${\ Displaystyle \ mathbf {x} _ {k}}$ ${\ Displaystyle \ kappa (A)}$${\ Displaystyle A}$${\ Displaystyle \ kappa (A)}$

Jeśli jest duża, hartowanie jest powszechnie stosowany w celu zastąpienia oryginalnego systemu z takimi, które jest mniejsze niż podano poniżej. ${\ Displaystyle \ kappa (A)}$${\ Displaystyle \ mathbf {topór} - \ mathbf {b} = 0}$${\ Displaystyle \ mathbf {M} ^ {-1} (\ mathbf {topór} - \ mathbf {b}) = 0}$${\ Displaystyle \ kappa (\ mathbf {M} ^ {-1} \ mathbf {A})}$${\ Displaystyle \ kappa (\ mathbf {A})}$

Twierdzenie o zbieżności

Zdefiniuj podzbiór wielomianów jako

${\ Displaystyle \ Pi _ {k} ^ {*}: = \ lewo \ lbrace \ p \ w \ pi _ {k} \ : \ p (0) = 1 \ \ prawo \ r nawias \ ,,}$

gdzie jest zbiorem wielomianów o maksymalnym stopniu . ${\ Displaystyle \ Pi _ {k}}$${\displaystyle k}$

Niech będzie iteracyjnym przybliżeniem dokładnego rozwiązania i zdefiniuj błędy jako . Teraz tempo zbieżności można przybliżyć jako ${\ Displaystyle \ lewo (\ mathbf {x} _ {k} \ po prawej) _ {k}}$${\ Displaystyle \ mathbf {x} _ {*}}$${\ Displaystyle \ mathbf {e} _ {k}: = \ mathbf {x} _ {k} - \ mathbf {x} _ {*}}$

${\ Displaystyle {\ zacząć {wyrównany} \ lewo \ | \ mathbf {e} _ {k} \ prawo \ | _ {\ mathbf {A}} i = \ min _ {p \ w \ pi _ {k} ^ {*}}\left\|p(\mathbf {A} )\mathbf {e} _{0}\right\|_{\mathbf {A} }\\&\leq \min _{p\in \ Pi _{k}^{*}}\,\max _{\lambda \in \sigma (\mathbf {A} )}|p(\lambda )|\ \left\|\mathbf {e} _{0 }\right\|_{\mathbf {A} }\\&\leq 2\left({\frac {{\sqrt {\kappa (\mathbf {A} )}}-1}{{\sqrt {\ kappa (\mathbf {A} )}}+1}\right)^{k}\ \left\|\mathbf {e} _{0}\right\|_{\mathbf {A} }\,, \end{wyrównany}}}$

gdzie oznacza widmo , a oznacza numer warunku . ${\ Displaystyle \ sigma (\ mathbf {A} )}$${\ Displaystyle \ kappa (\ mathbf {A})}$

Uwaga, ważny limit, kiedy ma tendencję do${\ Displaystyle \ kappa (\ mathbf {A})}$${\displaystyle \infty}$

${\ Displaystyle {\ Frac {{\ sqrt {\ kappa (\ mathbf {A} )}} -1 {{\ sqrt {\ kappa (\ mathbf {A} )}} +1}} \ około 1-{ \frac {2}{\sqrt {\kappa (\mathbf {A} )}}}\quad {\text{dla}}\quad \kappa (\mathbf {A} )\gg 1\,.}$

Ten limit pokazuje szybszy współczynnik zbieżności w porównaniu z iteracyjnymi metodami Jacobiego lub Gaussa-Seidela, które skalują się jako . ${\ Displaystyle \ około 1-{\ Frac {2} {\ kappa (\ mathbf {A}}}}}$

W twierdzeniu o zbieżności nie zakłada się błędu zaokrąglenia , ale wiązanie zbieżności jest powszechnie ważne w praktyce, jak teoretycznie wyjaśnia Anne Greenbaum .

Praktyczna konwergencja

Jeśli inicjuje się losowo, pierwszy etap iteracji jest często najszybszy, ponieważ błąd jest eliminowany w podprzestrzeni Kryłowa, która początkowo odzwierciedla mniejszą liczbę warunków efektywnych. Drugi etap zbieżności jest zwykle dobrze zdefiniowany przez teoretyczną zbieżność związaną z , ale może być superliniowy, w zależności od rozkładu widma macierzy i rozkładu widmowego błędu. W ostatnim etapie osiągana jest najmniejsza osiągalna dokładność i przeciągnięcia zbieżności lub metoda mogą nawet zacząć się rozchodzić. W typowych naukowych zastosowaniach obliczeniowych w formacie zmiennoprzecinkowym podwójnej precyzji dla macierzy o dużych rozmiarach metoda gradientu sprzężonego wykorzystuje kryteria zatrzymania z tolerancją, która kończy iteracje podczas pierwszego lub drugiego etapu. ${\displaystyle {\sqrt {\kappa (\mathbf {A})}}}$${\ Displaystyle A}$

Wstępnie uwarunkowana metoda gradientu koniugatów

W większości przypadków wstępne kondycjonowanie jest konieczne, aby zapewnić szybką konwergencję metody gradientu koniugatów. Wstępnie uwarunkowana metoda gradientu sprzężonego przyjmuje następującą postać:

${\ Displaystyle \ mathbf {r} _ {0}: = \ mathbf {b} - \ mathbf {topór} _ {0}}$

${\ Displaystyle \ mathbf {Z} _ {0}: = \ mathbf {M} ^ {-1} \ mathbf {R} _ {0}}$

${\ Displaystyle \ mathbf {p} _ {0}: = \ mathbf {z} _ {0}}$

${\displaystyle k:=0\,}$

powtarzać

${\ Displaystyle \ alfa _ {k}: = {\ Frac {\ mathbf {r} _ {k} ^ {\ mathsf {T}} \ mathbf {z} _ {k}} {\ mathbf {p} _ { k}^{\mathsf {T}}\mathbf {Ap} _{k}}}}$

${\ Displaystyle \ mathbf {x} _ {k + 1}: = \ mathbf {x} _ {k} + \ alfa _ {k} \ mathbf {p} _ {k}}$

${\ Displaystyle \ mathbf {r} _ {k + 1}: = \ mathbf {r} _ {k} - \ alfa _ {k} \ mathbf {ap} _ {k}}$

jeśli r _{k +1} jest wystarczająco małe, to koniec pętli wyjścia if

${\ Displaystyle \ mathbf {z} _ {k + 1}: = \ mathbf {M} ^ {-1} \ mathbf {r} _ {k + 1}}$

${\ Displaystyle \ beta _ {k}: = {\ Frac {\ mathbf {r} _ {k + 1} ^ {\ mathsf {T}} \ mathbf {z} _ {k + 1}} {\ mathbf { r} _{k}^{\mathsf {T}}\mathbf {z} _{k}}}}$

${\ Displaystyle \ mathbf {p} _ {k + 1}: = \ mathbf {z} _ {k + 1} + \ beta _ {k} \ mathbf {p} _ {k}}$

${\displaystyle k:=k+1\,}$

koniec powtarzania

Wynik to x _{k +1}

Powyższe sformułowanie jest równoważne zastosowaniu metody gradientu sprzężonego bez wstępnego kondycjonowania układu

${\ Displaystyle \ mathbf {E} ^ {-1} \ mathbf {A} (\ mathbf {E} ^ {-1}) ^ {\ mathsf {T}} \ mathbf {\ kapelusz {x}} = \ mathbf {E} ^{-1}\mathbf {b} }$

gdzie

${\ Displaystyle \ mathbf {EE} ^ {\ mathsf {T}} = \ mathbf {M} , \ qquad \ mathbf {\ kapelusz {x}} = \ mathbf {e} ^ {\ mathsf {T}} \ mathbf {x} .}$

Macierz warunków wstępnych M musi być symetryczna, dodatnio określona i stała, tj. nie może zmieniać się z iteracji na iterację. Jeśli którekolwiek z tych założeń na warunku wstępnym zostanie naruszone, zachowanie metody gradientu sprzężonego warunkowego może stać się nieprzewidywalne.

Przykładem powszechnie stosowanego warunku wstępnego jest niekompletna faktoryzacja Choleskiego .

Elastyczna, wstępnie uwarunkowana metoda gradientu koniugatów

W wymagających numerycznie aplikacjach stosuje się wyrafinowane uwarunkowania wstępne, które mogą prowadzić do zmiennych uwarunkowań wstępnych, zmieniających się między iteracjami. Nawet jeśli warunek wstępny jest symetryczny, dodatnio określony w każdej iteracji, to fakt, że może się on zmienić, powoduje, że powyższe argumenty są nieaktualne, a w testach praktycznych prowadzi do znacznego spowolnienia zbieżności algorytmu przedstawionego powyżej. Korzystanie z formuły Polaka-Ribière

${\ Displaystyle \ beta _ {k}: = {\ Frac {\ mathbf {r} _ {k + 1} ^ {\ mathsf {T}} \ lewo (\ mathbf {z} _ {k + 1} -\ mathbf {z} _{k}\right)}{\mathbf {r} _{k}^{\mathsf {T}}\mathbf {z} _{k}}}}$

zamiast formuły Fletchera-Reevesa

${\ Displaystyle \ beta _ {k}: = {\ Frac {\ mathbf {r} _ {k + 1} ^ {\ mathsf {T}} \ mathbf {z} _ {k + 1}} {\ mathbf { r} _{k}^{\mathsf {T}}\mathbf {z} _{k}}}}$

może radykalnie poprawić zbieżność w tym przypadku. Tę wersję wstępnie uwarunkowanej metody gradientu sprzężonego można nazwać elastyczną, ponieważ umożliwia zmienne uwarunkowanie wstępne. Wykazano również, że wersja elastyczna jest niezawodna, nawet jeśli kondycjoner wstępny nie jest symetryczny o wartości dodatniej (SPD).

Implementacja wersji elastycznej wymaga przechowywania dodatkowego wektora. Dla ustalonego warunku wstępnego SPD, więc obie formuły dla β _k są równoważne w arytmetyce dokładnej, tj. bez błędu zaokrąglenia . ${\ Displaystyle \ mathbf {r} _ {k + 1} ^ {\ mathsf {T}} \ mathbf {z} _ {k} = 0}$

Matematycznym wyjaśnieniem lepszego zachowania zbieżności metody ze wzorem Polaka-Ribière'a jest to, że metoda jest w tym przypadku lokalnie optymalna , w szczególności nie ma zbieżności wolniej niż lokalnie optymalna metoda największego opadania.

Vs. lokalnie optymalna metoda najbardziej stromego zjazdu

Zarówno w oryginalnej, jak i wstępnie uwarunkowanej metodzie gradientowej koniugatu wystarczy ustawić , aby były one lokalnie optymalne, przy użyciu metody przeszukiwania linii , metody najbardziej stromego opadania . Przy takim podstawieniu wektory p są zawsze takie same jak wektory z , więc nie ma potrzeby przechowywania wektorów p . Tak więc każda iteracja tych najbardziej stromych metod opadania jest nieco tańsza w porównaniu z metodami gradientu sprzężonego. Jednak te ostatnie zbiegają się szybciej, chyba że jest używany (wysoce) zmienny i/lub warunek wstępny inny niż SPD , patrz powyżej. ${\ Displaystyle \ beta _ {k}: = 0}$

Metoda gradientu sprzężonego jako optymalny kontroler sprzężenia zwrotnego dla podwójnego integratora

Metodę gradientu sprzężonego można również wyprowadzić przy użyciu optymalnej teorii sterowania . W tym podejściu metoda gradientu sprzężonego wypada jako optymalny regulator sprzężenia zwrotnego ,

$${\ Displaystyle u = k (x, v): = - \ gamma _ {a} \ nabla f (x) - \ gamma _ {b} v}$$

$${\displaystyle {\dot {x}}=v,\quad {\dot {v}}=u}$$

${\ Displaystyle \ gamma _ {a}}$

${\ Displaystyle \ gamma _ {b}}$

Gradient sprzężony na równaniach normalnych

Metodę gradientu sprzężonego można zastosować do dowolnej macierzy n -by- m , stosując ją do równań normalnych A ^T A i prawostronnego wektora A ^T b , ponieważ A ^T A jest symetryczną macierzą dodatnio-półokreśloną dla dowolnego A . Wynikiem jest gradient sprzężony na równaniach normalnych (CGNR).

A ^T Ax = A ^T b

Jako metoda iteracyjna nie jest konieczne tworzenie A ^T A bezpośrednio w pamięci, a jedynie wykonanie mnożenia macierz-wektor i transponowanie macierz-wektor. Dlatego CGNR jest szczególnie przydatny, gdy A jest macierzą rzadką, ponieważ te operacje są zwykle niezwykle wydajne. Jednak wadą tworzenia równań normalnych jest to, że liczba warunku κ( A ^T A ) jest równa κ ² ( A ), a więc szybkość zbieżności CGNR może być wolna, a jakość przybliżonego rozwiązania może być wrażliwa na zaokrąglenie błędy. Znalezienie dobrego kondycjonera jest często ważną częścią stosowania metody CGNR.

Zaproponowano kilka algorytmów (np. CGLS, LSQR). LSQR algorytm rzekomo ma najlepszą stabilność numeryczną podczas jest źle uwarunkowane, czyli posiada dużą liczbę warunek .

Metoda gradientu sprzężonego dla złożonych macierzy hermitowskich

Metodę gradientu sprzężonego z trywialną modyfikacją można rozszerzyć do rozwiązania, przy danej macierzy A i wektorze b, układu równań liniowych dla wektora x o wartościach zespolonych, gdzie A jest hermitowskim (tzn. A' = A) i dodatnim -definite matrix , a symbol ' oznacza transpozycję sprzężoną przy użyciu stylu MATLAB / GNU Octave . Trywialna modyfikacja polega po prostu na zastąpieniu wszędzie sprzężoną transpozycją rzeczywistą transpozycją . To podstawienie jest kompatybilne wstecz, ponieważ sprzężone transpozycja zamienia się w rzeczywistą transpozycję na wektorach i macierzach o wartościach rzeczywistych. Dostarczony powyżej przykładowy kod w MATLAB/GNU Octave działa już w przypadku złożonych macierzy hermitowskich, nie wymagając żadnych modyfikacji. ${\ Displaystyle \ mathbf {A} \ mathbf {x} = \ mathbf {b}}$

Zobacz też

Bibliografia

Dalsza lektura

• Atkinson, Kendell A. (1988). „Sekcja 8.9”. Wprowadzenie do analizy numerycznej (wyd. 2). John Wiley i Synowie. Numer ISBN 978-0-471-50023-0.
• Avriel, Mordechaj (2003). Programowanie nieliniowe: analiza i metody . Wydawnictwo Dover. Numer ISBN 978-0-486-43227-4.
• Golub, Gene H.; Van Pożyczka, Charles F. (2013). „Rozdział 11”. Obliczenia macierzowe (wyd. 4). Wydawnictwo Uniwersytetu Johnsa Hopkinsa. Numer ISBN 978-1-4214-0794-4.
• Saad, Yousef (2003-04-01). „Rozdział 6” . Metody iteracyjne dla rzadkich układów liniowych (wyd. 2). SYJAM. Numer ISBN 978-0-89871-534-7.

Zewnętrzne linki

• „Sprzężone gradienty, metoda” , Encyklopedia Matematyki , EMS Press , 2001 [1994]